2023年青岛版数学八年级上册《5.5 三角形内角和定理》课时练习（含答案）

2023年青岛版数学八年级上册

《5.5 三角形内角和定理》课时练习

一              、选择题

1.在△ABC中，∠A=∠B=∠C，则△ABC是(      )

A.锐角三角形  B.钝角三角形     C.直角三角形  D.无法确定

2.如图，在△ABC中，∠A=50°，∠ABC=70°，BD平分∠ABC，则∠BDC的度数是(  )

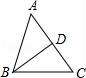
A.85°                      B.80°                      C.75°                      D.70°

3.如图，在△ABC中AC=BC，点D和E分别在AB和AC上，且AD=AE．连接DE，过点A的直线GH与DE平行，若∠C=40°，则∠GAD的度数为(　　)

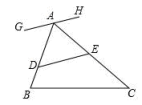
A．40°     B．45°       C．55°        D．70°

4.如图，点D在BC的延长线上，DE⊥AB于点E，交AC于点F．若∠A=35°，∠D=15°，

则∠ACB的度数为(　　)

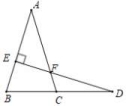
A．65°      B．70°      C．75°       D．85°

5.若一个三角形三个内角的度数之比是2∶3∶7，则这个三角形一定是(     )

A.直角三角形     B.锐角三角形    C.钝角三角形     D.不能确定

6.如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，则图中直角三角形有(    )

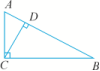
A.0个     B.1个      C.2个    D.3个

7.如图，△ABC中，AD是BC边上的高，AE，BF分别是∠BAC，∠ABC的平分线，∠BAC＝50°，∠ABC＝60°，则∠EAD＋∠ACD＝(     )

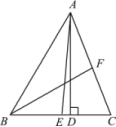
A.75°      B.80°      C.85°    D.90°

8.如图，在△ABC中，∠A＝52°，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，依此类推，∠ABD4与∠ACD4的角平分线交于点D5，则∠BD5C的度数是(    )

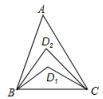
A.56°             B.60°             C.68°                D.94°

二              、填空题

9.在△ABC中，已知∠B＝55°，∠C＝80°，则∠A＝　   　.

10.直角三角形中两个锐角的差为20º，则两个锐角的度数分别为          .

11.将一副直角三角板如图摆放,点C在EF上,AC经过点D,已知∠A=∠EDF=90°,AB=AC,∠E=30°,∠BCE=40°,则∠CDF=          .

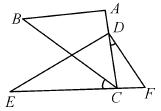
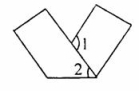
12.如图，将一个长方形纸条折成如图所示的形状，若已知∠2=65°，则∠1=__________。

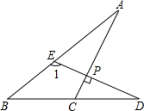
13.如图，在△ABC中，AD是∠BAC的平分线，E为AD上一点，且EF⊥BC于点F，若∠C＝35°，∠DEF＝15°，则∠B的度数为　   　.

14.当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为       ．

三              、解答题

15.如图，已知∠A=20°，∠B=27°，AC⊥DE，求∠1，∠D的度数．

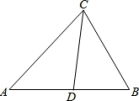
16.已知在△ABC中，∠A：∠B：∠C=2：3：4，CD是∠ACB平分线，求∠A和∠CDB的度数.

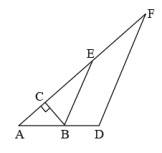
17.如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E.

（1）求∠CBE的度数；

（2）过点D作DF∥BE，交AC的延长线于点F，求∠F的度数.

18.如图,AD平分∠BAC，∠EAD=∠EDA.

（1）∠EAC与∠B相等吗？为什么？

（2）若∠B=50°,∠CAD：∠E=1：3，求∠E的度数.

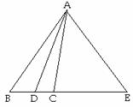
19.如图，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E．

（1）若∠B=35°，∠ACB=85°，求∠E的度数；

（2）当P点在线段AD上运动时，猜想∠E与∠B、∠ACB的数量关系，并证明你的结论．

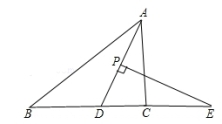
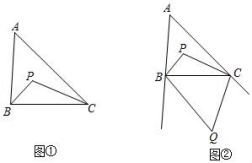
20.【探究】

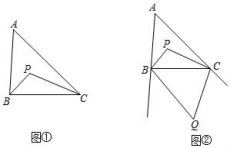
如图①，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P.

（1）若∠ABC=50°，∠ACB=80°，则∠A=　 　度，∠P=　 　度

（2）∠A与∠P的数量关系为　    　，并说明理由.

【应用】

如图②，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P.∠ABC的外角平分线与∠ACB的外角平分线相交于点Q.直接写出∠A与∠Q的数量关系为　      　.

参考答案

1.B

2.A

3.C

4.B

5.C

6.D

7.A

8.A

9.答案为：45°.

10.答案为：3.

11.答案为：25°

12.答案为：130  

13.答案为：65°.

14.答案为：30°.

15.解：∵AC⊥DE∴∠APE=90°

∵∠1=∠A+∠APE,∠A=20°∴∠1=110°

∵∠1+∠B+∠D=180°, ∠B=27°         ∴∠D=43°

16.解：∵在△ABC中，∠A：∠B：∠C=2：3：4，∠A+∠ACB+∠B=180°，

∴∠A=×180°=40°，∠ACB=×180°=80° 

∵CD是∠ACB平分线，∴∠ACD=0.5∠ACB=40°

∴∠CDB=∠A+∠ACD=40°+40°=80°

17.解：（1）∵在Rt△ABC中，∠ACB=90°，∠A=40°，

∴∠ABC=90°-∠A=50°，

∴∠CBD=130°.

∵BE是∠CBD的平分线，

∴∠CBE=0.5∠CBD=65°；

（2）∵∠ACB=90°，∠CBE=65°，

∴∠CEB=90°-65°=25°.

∵DF∥BE，

∴∠F=∠CEB=25°.

18.解：（1）相等.理由如下：∵AD平分∠BAC

∴∠BAD＝∠CAD

又∠EAD＝∠EDA

∴∠EAC＝∠EAD－∠CAD＝∠EDA－∠BAD＝∠B

（2）设∠CAD＝x°，则∠E＝3 x°，

由（1）有：∠EAC＝∠B＝50°

∴∠EAD＝∠EDA＝（x＋50）°

在△EAD中，∠E＋∠EAD＋∠EDA＝180°

∴3 x＋2（x＋50）＝180 

解得：x＝16

∴∠E＝48°

19.解：

解：

20.解：（1）∵∠ABC=50°，∠ACB=80°，

∴∠A=50°，

∵∠ABC的平分线与∠ACB的平分线相交于点P，

∴∠CBP=∠ABC，∠BCP=∠ACB，

∴∠BCP+∠CBP=（∠ABC+∠ACB）=×130°=65°，

∴∠P=180°﹣65°=115°，故答案为：50，115；

（2）.

证明：∵BP、CP分别平分∠ABC、∠ACB，

∴，，

∵∠A+∠ABC+∠ACB=180°∠P+∠PBC+∠PCB=180°，

∴，

∴，∴；

（3）.

理由：∵∠ABC的外角平分线与∠ACB的外角平分线相交于点Q，

∴∠CBQ=（180°﹣∠ABC）=90°﹣∠ABC，

∠BCQ=（180°﹣∠ACB）=90°﹣∠ACB，

∴△BCQ中，

∠Q=180°﹣（∠CBQ+∠BCQ）=180°﹣（90°﹣∠ABC+90°﹣∠ACB）

=（∠ABC+∠ACB），

又∵∠ABC+∠ACB=180°﹣∠A，

∴∠Q=（180°﹣∠A）=90°﹣∠A.