


数学八年级上册4.3 众数课后作业题
展开2023年青岛版数学八年级上册
《4.3 众数》课时练习
1.某校5名同学在“国学经典诵读”比赛中,成绩(单位:分)分别是86,95,97,90,88,这组数据的中位数是( )
A.97 B.90 C.95 D.88
2.已知数据:2,1,4,6,9,8,6,1,则这组数据的中位数是( )
A.4 B.6 C.5 D.4和6
3.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定9名同学参加决赛,他们的决赛成绩各不相同,其中小辉已经知道自己的成绩,但能否进前5名,他还必须清楚这9名同学成绩的( )
A.众数 B.平均数 C.中位数 D.方差
4.济南园博园对国庆黄金周七天假期的游客人数进行了统计,如表:
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
旅游人数万) | 1.5 | 2.2 | 2.2 | 3.8 | 1.5 | 2.2 | 0.6 |
其中平均数和中位数分别是( )
A.2和2.2 B.2和2 C.1.5和2.2 D.2.2和3.8
5.根据PM2.5空气质量标准:24小时PM2.5均值在0~35(微克/立方米)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表,这组PM2.5数据的中位数是( )
天数 | 3 | 1 | 1 | 1 | 1 |
PM2.5 | 18 | 20 | 21 | 29 | 30 |
A.21微克/立方米 B.20微克/立方米
C.19微克/立方米 D.18微克/立方米
6.某同学在今年的中考体育测试中选考跳绳.考前一周,他记录了自己五次跳绳的成绩(次数/分钟):247,253,247,255,263.这五次成绩的平均数和中位数分别是( )
A.253,253 B.255,253 C.253,247 D.255,247
7.某班九个合作学习小组的人数分别为5,5,5,6,x,7,7,7,8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.7 B.6 C.5. 5 D.5
8.喜迎建党 100 周年,某校将举办小合唱比赛,七个参赛小组人数如下:5,5,6,7,x,7,8.已知这组数平均数是6,则这组数据的中位数( )
A.5 B.5.5 C.6 D.7
10.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为________.
11.某次数学测试,某班一个学习小组的六位同学的成绩如下:84、75、75、92、86、99,则这六位同学成绩的中位数是 .
12.如果一组数据从小到大依次排列为x1,x2,x3,x4,x5,且x1,x2,x3的平均数为25,x3,x4,x5的平均数为35,x1,x2,x3,x4,x5的平均数是30,那么这组数据的中位数为________.
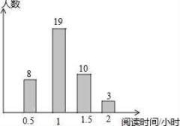
13.为响应“书香成都”建设号召,在全校形成良好的人文阅读风尚,成都市某中学随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数是 小时.
14.小刚在最近的一次数学测试中考了93分,从而使本学期之前所有的数学测试平均分由73分提高到78分,他要想在下次考试中把本学期平均分提高到80分以上,下次考试他至少要考 分.
三 、解答题
15.在某一中学田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(米) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 | 1 | 1 |
分别求这些运动员成绩的中位数和平均数(结果保留到小数点后第2位).
16.为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
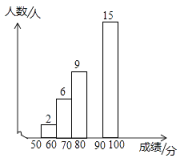
汉字听写大赛成绩分数段统计表汉字听写大赛成绩分数段条形统计图
分数段 | 频数 |
50≤x<60 | 2 |
60≤x<70 | 6 |
70≤x<80 | 9 |
80≤x<90 | 18 |
90≤x≤100 | 15 |
(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在 的分数段中;这次抽取的学生成绩在60≤x<70的分数段的人数占抽取人数的百分比是 .
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?
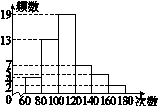
17.某中学对全校学生60秒跳绳的次数进行了统计,全校学生60秒跳绳的平均次数是100次,某班体育委员统计了全班50名学生60秒跳绳的成绩,列出的频数分布直方图如图所示(每个分组包括左端点,不包括右端点).
(1)该班学生60秒跳绳的平均次数至少是多少?是否超过全校平均次数?
(2)该班一个学生说:“我的跳绳成绩在我班是中位数.”请你给出该生跳绳成绩所在的范围.
18.为了增强学生的身体素质,教育部门规定学生每天参加体育锻炼的时间不少于1小时,为了了解学生参加体育锻炼的情况,抽样调查了900名学生每天参加体育锻炼的时间,并将调查结果制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
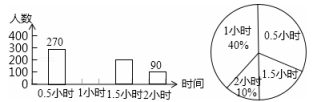
(1)请补充这次调查参加体育锻炼时间为1小时的频数直方图;
(2)求这次调查参加体育锻炼时间为1.5小时的人数;
(3)这次调查参加体育锻炼时间的中位数是多少?
19.争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分)
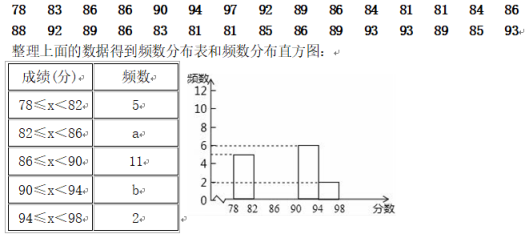
回答下列问题:
(1)以上30个数据中,中位数是 ;频数分布表中a= ;b= ;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.
20.某企业有4000名职工,从中随机抽取350人,按年龄分布和对“抢红包”所持态度情况进行了调查,并将调查结果绘成了条形统计图和扇形统计图.

(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?
(3)请估计该企业“从不(抢红包)”的人数是多少?
15.解:本题中人数的总个数是17人,奇数,从小到大排列后第9名运动员的成绩是1.70(米);
平均数是:(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80+1.85+1.90)÷17
=(3+4.8+3.3+5.1+7+1.8+1.85+1.9)÷17
=28.75÷17
≈1.69(米),
答:这些运动员成绩的中位数是1.70米,平均数大约是1.69米.

(2)∵被调查的总人数为2+6+9+18+15=50人,而第25、26个数据均落在80≤x<90,
∴这次抽取的学生成绩的中位数在80≤x<90的分数段中,
这次抽取的学生成绩在60≤x<70的分数段的人数占抽取人数的百分比是![]() ×100%=12%,
×100%=12%,
故答案为:80≤x<90,12%;
(3)105.
答:该年级参加这次比赛的学生中成绩“优”等的约有105人.
(60×4+80×13+100×19+120×7+140×5+160×2)÷50=100.8(次).
因为100.8>100,
所以超过全校平均次数.
(2)这个学生的跳绳成绩在该班是中位数,
由4+13+19=36,可知该生跳绳成绩一定在100~120次范围内.
锻炼时间是1小时的人数是900×40%=360(人),补图略.
(2)这次调查参加体育锻炼时间为1.5小时的人数是900-270-360-90=180(人).
(3)参加体育锻炼时间的中位数是1小时.
19.解:(1)根据题意排列得:78,81,81,81,81,83,83,84,84,85,85,86,86,86,86,86,86,88,89,89,89,89,90,92,92,93,93,93,94,97,
可得中位数为86,
频数分布表中a=6,b=6;故答案为:86;6;6;
(2)补全频数直方图,如图所示:
(3)根据题意得:300×![]() =190,
=190,
则该校七年级300名学生中,达到优秀等级的人数为190人.
20.解:(1)∵抽取350人,∴中位数是175和176的平均数,
∴中位数所在的年龄段是25-35;
(2)这次接受调查的职工中“参与抢红包”的人数是:350×(40%+22%)=217人;
(3)估计该企业“从不(抢红包)”的人数是:4000×(1-40%-22%)=1520人.
数学第4章 数据分析4.3 众数精品课后测评: 这是一份数学第4章 数据分析4.3 众数精品课后测评,共8页。试卷主要包含了3 众数》同步练习等内容,欢迎下载使用。
初中数学青岛版八年级上册4.3 众数课后作业题: 这是一份初中数学青岛版八年级上册4.3 众数课后作业题,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
青岛版八年级上册4.3 众数精品复习练习题: 这是一份青岛版八年级上册4.3 众数精品复习练习题,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













