数学人教A版 (2019)4.4 对数函数导学案

2021-2022（上） 全品学练考 高中数学 必修第一册 RJA（新教材）

4.4　对数函数

4.4.1　对数函数的概念

【课前预习】

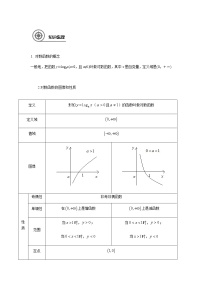
知识点

logax　(0,+∞)

诊断分析

1.(1)×　(2) √　(3)×　[解析] (1)对数函数中自变量x在真数的位置上,所以错误.

(2)在对数函数y=logax中,logax的系数必须是1,而y=2log2x可化为y=lox,所以正确.

(3)由x+1>0,可得x>-1,所以函数的定义域为(-1,+∞),所以错误.

2.解:不能.由y=logax,得x=ay,

在指数函数中底数a需要满足a>0且a≠1,

故在对数函数的解析式中,a不能等于0或小于0.

【课中探究】

探究点一

例1　(1)5　(2)②　[解析] (1)由对数函数的定义可知解得a=5.

(2)①log2x的系数是3,不是1,不是对数函数.

②符合对数函数的结构形式,是对数函数.

③自变量在底数位置上,不是对数函数.

④对数式log2x后又加上1,不是对数函数.

探究点二

例2　(1)A　(2)D　[解析] (1)由题意得解得-3<x<0,所以函数f(x)=的定义域是(-3,0).故选A.

(2)由题意得解得0<x≤1,所以函数f(x)的定义域是(0,1],故选D.

变式　解:(1)要使函数有意义,需满足解得x>2且x≠3.

所以函数的定义域为(2,3)∪(3,+∞).

(2)要使函数有意义,需满足解得-1<x<0或0<x<4.

所以函数的定义域为(-1,0)∪(0,4).

(3)要使函数有意义,需满足27-3x>0,得3x<27=33,

由指数函数的单调性得x<3.

所以函数的定义域为(-∞,3).

探究点三

例3　解:设过滤y次后杂质含量为x,则x=0.021-y,

即50x=y,则y=lo(50x),

令x=0.001,得y=lo0.05=lo=-==≈≈10.42,

所以至少应过滤11次才能使产品达到市场要求.

变式　解:设从2017年开始,经过y年后该公司全年投入的研发资金为x万元,

则x=130×(1+12%)y,即=1.12y,所以y=log1.12,

令x=200,得y=log1.12=log1.12=≈3.8,

所以2021年该公司全年投入的研发资金开始超过200万元.

【课堂评价】

1.B　[解析] 符合对数函数的定义的只有③④.故选B.

2.D　[解析] 要使函数y=lg(3x-2)有意义,需满足3x-2>0,解得x>,故选D.

3.B　[解析] 根据函数解析式得f=log2=-2,所以ff=f(-2)=2-2=.故选B.

4.B　[解析] 方法一:因为f(10x)=x,所以f(3)=f(10lg 3)=lg 3,故选B.

方法二:设t=10x,则x=lg t,所以f(t)=lg t,所以f(3)=lg 3,故选B.

5.5　[解析] 由对数函数的定义可知解得a=5.