初中数学北师大版七年级下册5 平方差公式完美版ppt课件

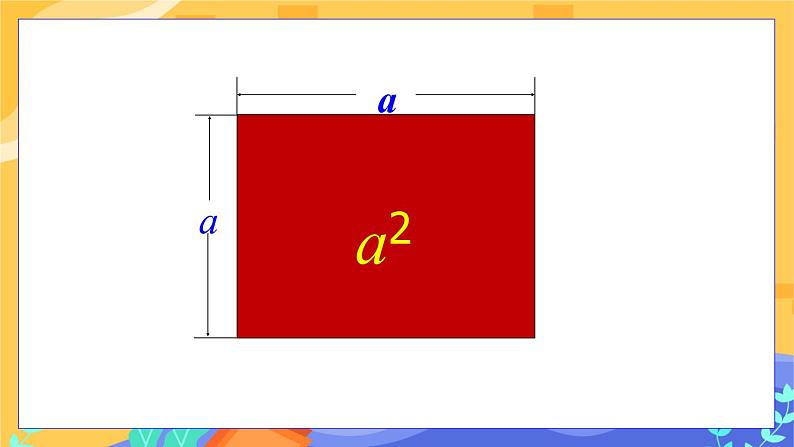
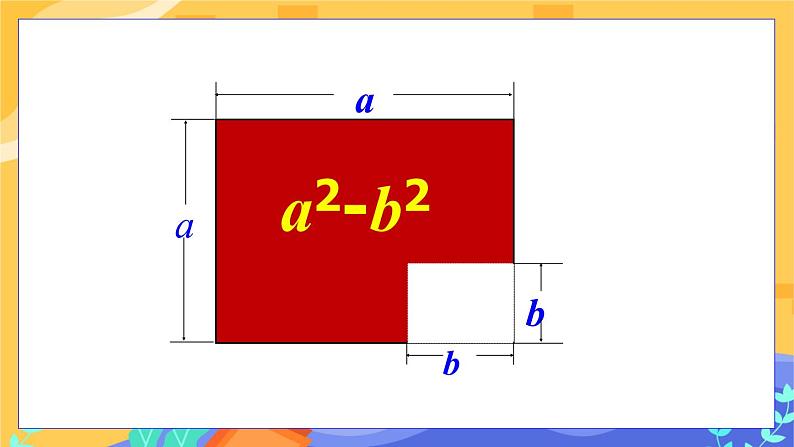
教学目标

1. 进一步使学生理解平方差公式的结构特征，能运用公式进行简便

运算；

2. 经历几何图形说明公式意义的过程，引导学生体会数形结合的思想

方法.

教学重难点

重点：平方差公式的应用及推广

难点：平方差公式的应用及推广

复习巩固

多项式与多项式是如何相乘的？

教学过程

导入新课

如图1所示，边长为的大正方形中有一个边长为的小正方形，小明将阴影部分拼成了一个长方形(如图2) ，你能表示出剪拼前后的图形的面积关系吗？

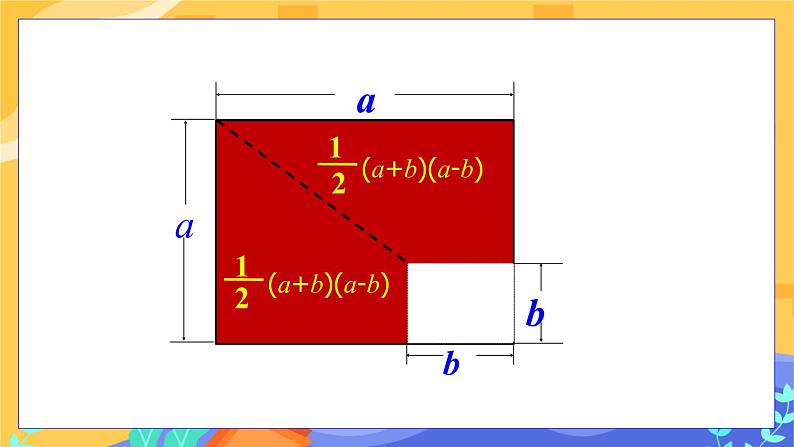
              图1                   图2

探究新知

【实践探究，交流新知】

【教师引导，学生讨论】

1.平方差公式几何意义的探究

图1中阴影部分的面积为：a2－b2；

如图2，阴影部分长方形的长和宽分别是a＋b，a－b，它的面积是(a＋b)(a－b)；

图1                   图2

通过上面的结果，你能验证平方差公式吗？说一说验证的理由．

解：能．理由：阴影部分的面积是不变的，即(a＋b)(a－b)＝a2－b2.

【深入思考】只通过图1你能验证平方差公式吗？

(a＋b)(a－b)＝a2－b2

2.利用平方差公式探索规律

想一想，计算下列各式，并观察它们的共同特点：

【提问】从以上的过程中，你发现了什么规律？

答：两个连续奇数的积，等于这两个奇数中间的那个偶数的平方与1的差.

【提问】如何用字母表示这一规律？

字母表示：(n－1)(n＋1)＝n2－1(n为偶数)．

【提问】你能说明它的正确性吗？

证明：根据平方差公式，得(n－1)(n＋1)＝n2－12＝n2－1.

【合作探究，解决问题】

【小组讨论】

例1  用平方差公式进行计算：

(1)103×97;  (2)118×122.

解：（1）103×97

＝（100+3）（100-3）

＝1002-32

＝9 991；

（2）118×122

＝（120-2）（120+2）

＝1202-22

＝14 396.

【总结】有时将所给式子进行恰当的变形，将其变化为两数和与两数差的积的形式，可以使复杂的计算简单化，以达到事半功倍的效果.

【拓展延伸】

例2计算：

（1）a2(a+b)( a-b)+a2b2;

（2）（2x-5）（2x+5）-2x（2x-3）.

解：（1）a2（a+b）（a-b）+a2b2

=a2（a2-b2）+a2b2

=a4-a2b2+a2b2

=a4;

（2）（2x-5）（2x+5）-2x（2x-3）

=（2x）2-25-（4x2-6x）

=4x2-25-4x2+6x

=6x-25.

【教师提问】若=(2+1)(22+1)(24+1)，则的值是多少？

【教师引导学生思考】如何简便运算？可以应用平方差公式吗？如何

变形？

【学生活动】小组讨论，互动探讨.

答：(2+1)(22+1)(24+1)

     [(2－1)(2+1)(22+1)(24+1)]÷(2－1)

      [(22－1)(22+1)(24+1)]÷(2－1)

     [(24－1)(24+1)]÷(2－1)

     (28－1)÷(2－1)

     28－1．

课堂小结

平方差公式

两个数的和与这两个数的差的积，等于这两个数的平方差.

符号表示：－2.

几何图形验证：同一图形变形后用不同的形式表示面积.

应用：变形进行简便运算

板书设计

平方差公式

1.几何图形验证关键：同一图形变形后用不同的形式表示面积.

2. 两个连续奇数的积，等于这两个奇数中间的那个偶数的平方与1的

差， 即＝2－1（n为偶数）.

3.应用：简便运算是将式子进行恰当的变形转化为两数和与两数差的

积的形式.