北师大版七年级下册5 平方差公式优秀课件ppt

这是一份北师大版七年级下册5 平方差公式优秀课件ppt，文件包含152平方差公式pptx、152平方差公式教学设计docx等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

1.问：平方差公式是怎样的？
(a+b)(a−b)=a2−b2
2.利用平方差公式计算：（1）(2x+7b)(2x–7b)； （2）(－m+3n)(m+3n).
某同学在计算97×103时将其变成(100-3)(100+3)并很快得出结果，你知道他运用了什么知识吗？这节课我们一起来探讨上述计算的规律.
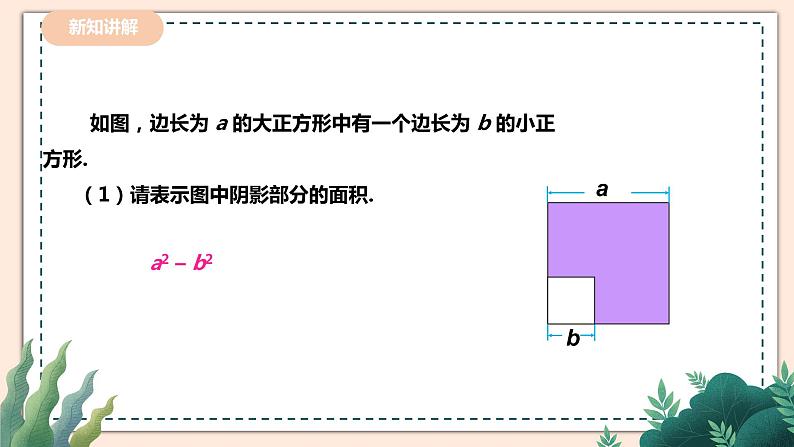
如图，边长为 a 的大正方形中有一个边长为 b 的小正方形. （1）请表示图中阴影部分的面积.
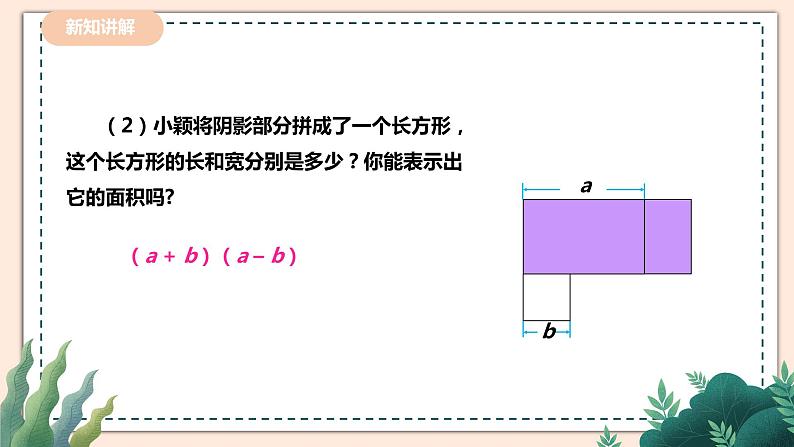
（2）小颖将阴影部分拼成了一个长方形，这个长方形的长和宽分别是多少？你能表示出它的面积吗?
（a + b）（a – b）
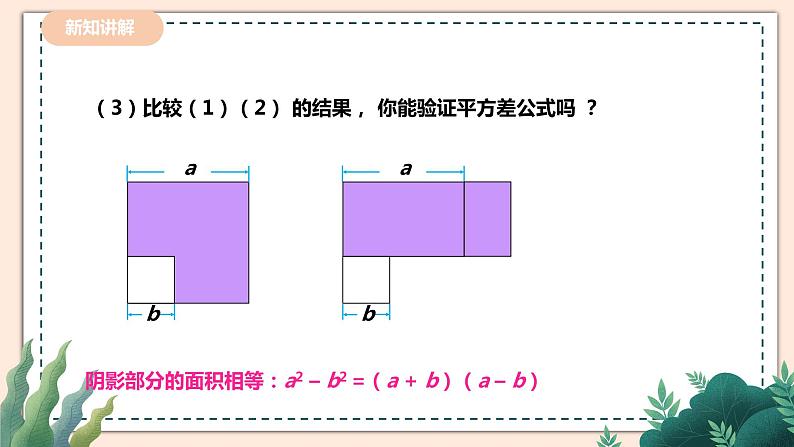
（3）比较（1）（2） 的结果， 你能验证平方差公式吗 ？
阴影部分的面积相等：a2 – b2 =（a + b）（a – b）
（1）计算下列各组算式， 并观察它们的共同特点：
（一个自然数的平方比它相邻两数的积大1.）
（2）从以上的过程中，你发现了什么规律？请用字母表示这一规律，你能说明它的正确性吗？
(a+1)(a−1)=a2−1
例1 计算:(1) 103×97; (2) 118×122.
解: 103×97=(100+3)(100－3)= 1002－32=10000 – 9=9991；
解: 118×122=(120－2)(120＋2)= 1202－22=14400－4=14396.
本题运用了转化思想求解．运用平方差公式计算两数乘积问题，关键是找到这两个数的平均数，再将原两个数与这个平均数进行比较变形成两数的和与这两数的差的积的形式，再用平方差公式可求解．
解: (1) 102×98
=10000 – 4
=（100＋2）(100－2)
(2) 原式=（50＋1）(50－1)
（1）a2(a + b) (a – b) + a2b2；
（2）(2x – 5) (2x + 5) – 2x(2x – 3).
解：(1) a2(a+b)(a-b) +a2b2；=a2(a2-b2) +a2b2=a4-a2b2 +a2b2=a4 ；
(2) (2x-5)(2x+5)-2x (2x-3). = (2x)2-25-(4x2 -6x) = 4x2-25-4x2 +6x = 6x-25
对于任意的正整数n，整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的整数倍吗？
即(3n+1)(3n-1)-(3-n)(3+n)的值是10的倍数．
解：原式＝9n2-1-(9-n2)
因为(10n2-10)÷10=n2-1.
在探究整除性或倍数问题时，一般先将代数式化为最简，然后根据结果的特征，判断其是否具有整除性或倍数关系．
1.如图1，将边长为x的大正方形剪去一个边长为1的小正方形（阴影部分），并将剩余部分沿虚线剪开，得到两个长方形，再将这两个长方形拼成图2所示长方形．这两个图能解释下列哪个等式（　　）A．x2﹣2x+1＝（x-1）2B．x2-1＝（x+1）（x-1）C．x2+2x+1＝（x+1）2D．x2-x＝x（x-1）
2.计算20162－2015×2017的结果是(　　)A．1　　　 B．－1　　　C．2　　　 D．－23.97×103=( )×( )=( ).4.(x+6)(x－6)－x(x－9)=0的解是______.
(1)（a – 2)(a + 2)(a2 + 4)
=（a2 – 4）（a2 + 4）= a4 – 16
(2)（x + y + 1）（x – y – 1）
= [ x +（y + 1）][ x –（y + 1）]
= x2 – （y + 1）2
= x2 – y2 – 2y – 1
(3)(a + b + c) (a + b – c)
= (a + b)2 – c2
= a2 + 2ab + b2 – c2
(4)20152 – 2014×2016
= 20152 – (2015 – 1)×(2015 + 1)
= 20152 – (20152 – 12)
6．已知a－b＝5，ab＝4.(1)求3a2＋3b2的值；
解：3a2＋3b2＝3(a2＋b2)＝3[(a－b)2＋2ab] ＝3×(52＋2×4)＝3×33＝99.
(2)求(a＋b)2的值．
由(1)可知a2＋b2＝33，所以(a＋b)2＝a2＋b2＋2ab＝33＋2×4＝41.
1.课本第22页习题1.10第1、2题
在整式的乘法中只有符合公式要求的乘法才能用公式计算，其余的运算仍按乘法法则进行.