初中数学人教版八年级上册第十二章 全等三角形综合与测试测试题

绝密★启用前

2022人教版八年级数学上册第12章综合测试-带答案和解析

副标题

考试范围：xxx；考试时间：100分钟；命题人：xxx

注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。

第I卷（选择题）

一、选择题（本大题共9小题，共27.0分。在每小题列出的选项中，选出符合题目的一项）

1. 如下图所示，在中，，延长至点，使，过作于点，交于点，若，则的度数是(    )

A.
B.
C.
D.

2. 如下图所示，、是锐角的高，相交于点，若，，，则的长为(    )

A.
B.
C.
D.

3. 如图，，于点，于点，，若，则的度数为(    )

A.
B.
C.
D.

4. 如图，，只添加一个条件，使≌下列条件中正确的是(    )

A.  B.  C.  D.

5. 如图是一种测量工具，点是两根钢条、的中点，并能绕点转动由三角形全等可得内槽宽与相等，其中的依据是(    )

A.
B.
C.
D.

6. 如图，，，添加一个条件，不能保证≌的是(    )

A.
B.
C.
D.

7. 如图，在中，，平分，于点，有下列结论：
   平分，其中结论正确的个数为(    )

A.
B.
C.
D.

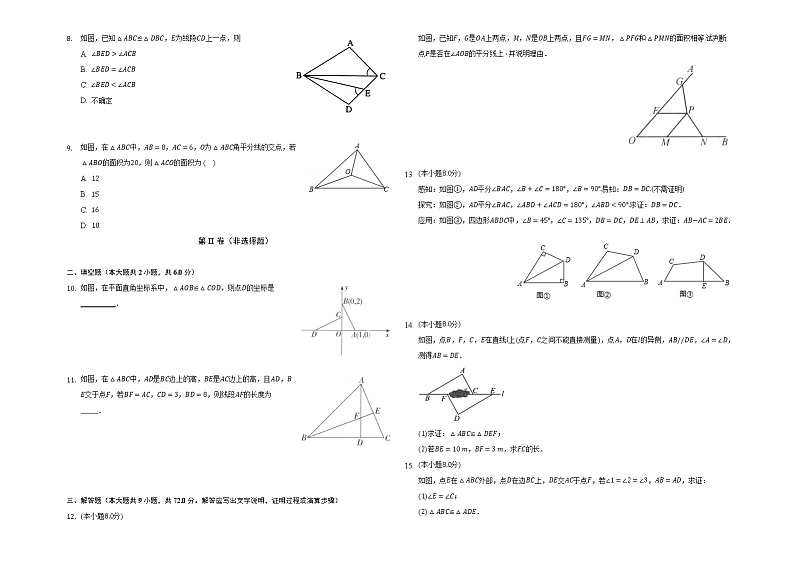
8. 如图，已知≌，为线段上一点，则

A.
B.
C.
D. 不确定

9. 如图，在中，，，为角平分线的交点，若的面积为，则的面积为(    )

A.
B.
C.
D.

第II卷（非选择题）

二、填空题（本大题共2小题，共6.0分）

10. 如图，在平面直角坐标系中，，则点的坐标是__________．

11. 如图，在中，是边上的高，是边上的高，且，交于点，若，，，则线段的长度为          ．

三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

12. 本小题分

如图，已知，是上两点，，是上两点，且，和的面积相等试判断点是否在的平分线上并说明理由．

13. 本小题分
    感知：如图，平分，，易知：不需证明
    探究：如图，平分，，求证：．
    应用：如图，四边形中，，，，，求证：．
     

14. 本小题分

如图，点，，，在直线上点，之间不能直接测量，点，在的异侧，，，测得．

求证：≌；

若，，求的长．

15. 本小题分
    如图，点在外部，点在边上，交于点，若，，求证：
    ；
    ≌．

16. 本小题分
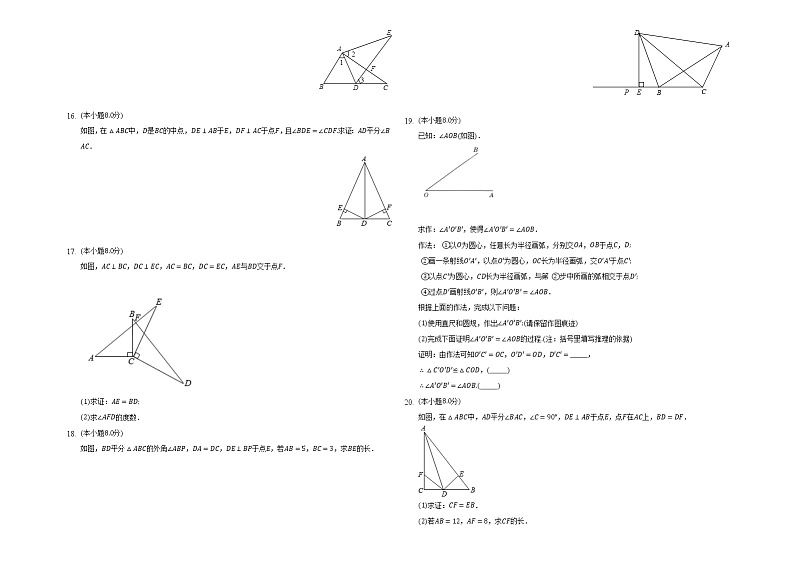
    如图，在中，是的中点，于，于点，且求证：平分．

17. 本小题分
    如图，，，，，与交于点．
    
     

求证：

求的度数．

18. 本小题分
    如图，平分的外角，，于点，若，，求的长．

19. 本小题分

已知：如图．

求作：，使得．

作法：以为圆心，任意长为半径画弧，分别交，于点，

画一条射线，以点为圆心，长为半径画弧，交于点

以点为圆心，长为半径画弧，与第步中所画的弧相交于点

过点画射线，则．

根据上面的作法，完成以下问题：

使用直尺和圆规，作出请保留作图痕迹

完成下面证明的过程注：括号里填写推理的依据

证明：由作法可知，，          ，

，          

20. 本小题分
    如图，在中，平分，，于点，点在上，．
    
    求证：．
    若，，求的长．
    

答案和解析

1.【答案】 

【解析】

【分析】
本题考查全等三角形的判定和性质，直角三角形的性质等知识，解题的关键是熟练掌握全等三角形的判定和性质，属于中考常考题型． 首先证明≌，推出，再证明≌，推出，在中求得，从而得到的度数，再根据四边形的内角和是求得，即可解决问题．
【解答】
解：，
，
在和中，

≌，
，
在和中，
，
≌，
，
在中，，
，
，
．  

2.【答案】 

【解析】

【分析】
本题主要考查了全等三角形的判定和性质，证明三角形的全等是解此题的关键．
首先证明，再根据，，得出≌，即可得出的长． 
【解答】
解：，是的高，
，
，，
，
在与中， 
， 
≌， 
，，，
 
故选B．  

3.【答案】 

【解析】解：，
，
，，
，
在和中，
，
≌，
，
，
故选：．
由知，根据“”证和得，从而由可得答案．
本题主要考查全等三角形的判定与性质及直角三角形的性质，熟练掌握全等三角形的判定和性质是解题的关键．
 

4.【答案】 

【解析】解：若添加，则由可得，≌，即可得到，依据即可得出≌．
若添加，则由可得，≌，即可得到，依据即可得出≌．
若添加，则由可得，≌，即可得到，依据即可得出≌．
若添加，则不能得到≌；
故选：．
全等三角形的判定，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．
本题主要考查了全等三角形的判定，在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．
 

5.【答案】 

【解析】解： 是、的中点，
，．
在和中，
，
故选C．
 

6.【答案】 

【解析】解：，，，符合全等三角形的判定定理，能推出≌，故本选项不符合题意；
B.，，，符合全等三角形的判定定理，能推出≌，故本选项不符合题意；
C.，
，
即，
，，，符合全等三角形的判定定理，能推出≌，故本选项不符合题意；
D.，，，不符合全等三角形的判定定理，不能推出≌，故本选项符合题意；
故选：．
根据全等三角形的判定定理逐个判断即可．
本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有，，，，两直角三角形全等还有．
 

7.【答案】 

【解析】 解：在中，，平分，，，正确
在和中，
，
，，
平分，正确
，，正确
，，
，正确

，，且，，正确．
结论正确的个数为，故选A．

8.【答案】 

【解析】

【分析】
本题主要考查的是全等三角形的性质，三角形的外角性质的有关知识，利用全等三角形的性质得到，然后利用三角形的外角性质进行求解即可．
【解答】
解：≌，
，
，
，
，故A正确；B错误；C错误；D错误．
故选A．  

9.【答案】 

【解析】

【分析】
本题主要考查了角平分线的性质，根据其性质可以得到点到，的距离相等，即三角形与三角形的高相等，据此可以得到结论．
【解答】
解：平分，
点到，的距离相等，设其距离为，则三角形与三角形的高为，
的面积为，
，
，
解得，
的面积，
故选B．  

10.【答案】 

【解析】

【分析】
本题考查了全等三角形的性质，主要利用了全等三角形对应边相等的性质，是基础题．
根据全等三角形对应边相等可得，然后写出点的坐标即可．
【解答】
解：≌，
，
点的坐标是．
故答案为：．
  

11.【答案】 

【解析】解：是边上的高，是边上的高，

，

，，

，

在和中，

，

，，

，

故答案为

12.【答案】解：点在的平分线上．
理由：过点作于点，于点．

，，，
．
又，
，
与在的平分线上． 

【解析】略
 

13.【答案】证明：，，
，
平分，
，
在和中，，
≌，
；
证明：作于，于，如图所示：
平分，，，
，
，，
，
在和中，，
≌，
；
证明：连接，作于，如图所示：
，
，
，
，
在和中，，
≌，
，，
在和中，，
≌，
，
，
． 

【解析】由证明≌，即可得出结论；
作于，于，由证明≌，即可得出结论；
连接作于首先由证明≌，再由证明≌即可解决问题．
本题是四边形综合题，主要考查了全等三角形的判定和性质、角平分线的性质等知识，解题的关键是添加辅助线，构造全等三角形．
 

14.【答案】证明：，

，
在与中

≌；
解：≌，
，
，
，
，，
． 

【解析】本题考查全等三角形的判定和性质、平行线的性质等知识，解题的关键是正确寻找全等三角形的条件，记住平行线的判定方法，属于基础题，中考常考题型．
先证明，再根据即可证明；
根据全等三角形的性质即可解答．
 

15.【答案】证明：，，
，
即．
，
，
即．
，，
≌． 

【解析】根据三角形内角和定理可得；
由已知可得，又因为，所以根据可判定≌．
此题考查学生对三角形内角和定理及全等三角形的判定的理解及运用．
三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
 

16.【答案】证明：，，
，
是的中点，
，
在和中，
，
≌，
，
于，于点，
平分． 

【解析】求出，，根据全等三角形的判定得出≌，根据全等三角形的性质得出，再推出答案即可．
本题考查了全等三角形的性质和判定，角平分线的判定等知识点，能求出是解此题的关键．
 

17.【答案】解：，，
，
，
在和中，
，
≌，
；
，
，
≌，
，
，
，
．
 

【解析】先证明，再证明≌便可得；
由全等三角形得，由，推出，可得．
本题考查全等三角形的判定和性质，三角形内角和定理，三角形外角定理，解题的关键是正确寻找全等三角形全等的条件，灵活运用所学知识解决问题，属于中考常考题型．
 

18.【答案】解：过点作的垂线交于点

平分的外角，，
．
在和中，

≌．
，
在和中，

≌．
．
由图象易知：
，，
，
，
而，
．
故BE． 

【解析】过点作的垂线交于点，分别证≌和≌，再利用全等三角形的性质即可求出的长．
本题考查全等三角形的性质与判定，通过观察题目，正确作出辅助线并通过三角形全等去推理是解题关键．
 

19.【答案】解：如图所示，即为所求．

全等三角形的对应角相等

【解析】略
 

20.【答案】证明：平分，，于，
，
在与中，

≌，
；
解：设，则，
平分，，
，
在与中，

≌，
，
即，
解得，
即． 

【解析】本题考查的是角平分线的性质，直角三角形全等的判定与性质，熟知角平分线上的点到角两边的距离相等是解答此题的关键．
根据角平分线的性质“角平分线上的点到角的两边的距离相等”，可得点到的距离点到的距离即，再根据证明≌，从而得出；
设，则，再根据题意得出≌，进而可得出结论．