数学八年级上册3.2 勾股定理的逆定理优质课课件ppt

这是一份数学八年级上册3.2 勾股定理的逆定理优质课课件ppt，文件包含32勾股定理的逆定理pptx、32勾股定理的逆定理docx等2份课件配套教学资源，其中PPT共31页， 欢迎下载使用。


3.2 勾股定理的逆定理
苏科版 八年级上册数学
第三章 勾股定理
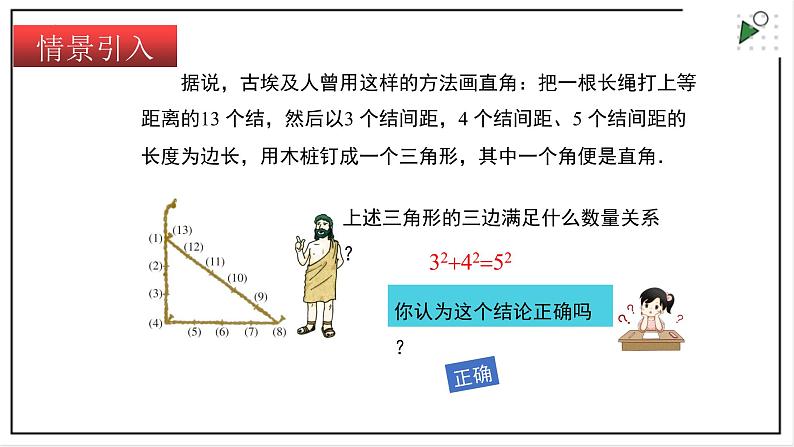
你认为这个结论正确吗？
　据说，古埃及人曾用这样的方法画直角：把一根长绳打上等距离的13 个结，然后以3 个结间距，4 个结间距、5 个结间距的长度为边长，用木桩钉成一个三角形，其中一个角便是直角．
上述三角形的三边满足什么数量关系？
324252
正确
情景引入
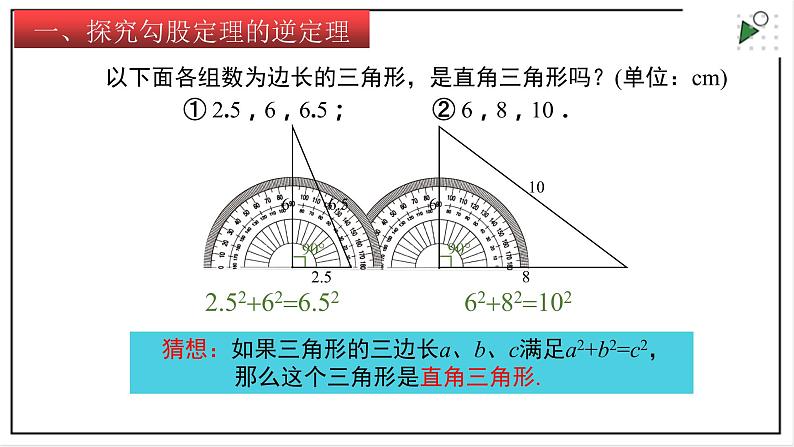
① 2.5，6，6.5； ② 6，8，10．
以下面各组数为边长的三角形，是直角三角形吗？(单位：cm)
2.5
6
① 2.5，6，6.5； ② 6，8，10．
以下面各组数为边长的三角形，是直角三角形吗？(单位：cm)
6.5
8
6
10
90°
90°
2.52626.52
6282102
猜想：如果三角形的三边长a、b、c满足a2+b2=c2， 那么这个三角形是直角三角形.
一、探究勾股定理的逆定理
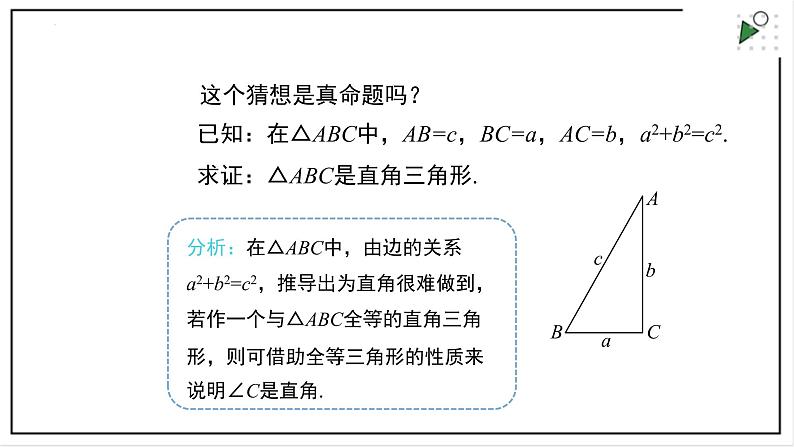
这个猜想是真命题吗？
分析：在△ABC中，由边的关系a2+b2=c2，推导出为直角很难做到，若作一个与△ABC全等的直角三角形，则可借助全等三角形的性质来说明∠C是直角.
已知：在△ABC中，AB=c，BC=a，AC=b，a2+b2=c2.求证：△ABC是直角三角形.
已知：在△ABC中，AB=c，BC=a，AC=b，a2+b2=c2.求证：△ABC是直角三角形.
证明：如图，作△A'B'C'，使∠C'=90°， B'C'=a，A'C'=b.
由勾股定理可得A'B'2=a2+b2.
∵a2+b2=c2，∴A'B'2=c2.
在△ABC和△A'B'C'中，
∵AB=A'B'=c，BC=B'C'=a，AC=A'C'=b.
∴△ABC≌△A'B'C'(SSS).
∴∠C'=∠C=90°(全等三角形的对应角相等).
c
即△ABC是直角三角形.
可以利用这个定理判定一个三角形是否为直角三角形.
这个命题是真命题，
也是一个定理，
如果三角形的三边长a、b、c满足a2+b2=c2，那么这个三角形是直角三角形.
勾股定理的逆命题
例1.△ABC中A， B， C的对边分别是a，b，c，则下列命题中的假命题是( ) A.如果CBA，则△ABC是直角三角形； B.如果c2=b2a2，则△ABC是直角三角形，且C90°； C.如果(ca)(ca)=b2，则△ABC是直角三角形； D.如果A  B  C=5  2  3，则△ABC是直角三角形.
B
分析：对于B选项，c2=b2a2
a2c2=b2
△ABC是直角三角形，b是最长边.
B90°
下面以a，b，c为边长的三角形是不是直角三角形？
(1) a5，b12，c13；
(2) a6，b7，c8；
是
不是
是
52+122132
62+7282
练一练
二、勾股数
常见勾股数：
3，4，5；5，12，13；6，8，10；7，24，25；8，15，17；9，40，41；10，24，26等等.
勾股数拓展性质：
一组勾股数，都扩大相同倍数k，得到一组新数，这组数同样是勾股数.
我们知道3,4,5是一组勾股数，那么3k,4k,5k（k是正整数）也是一组勾股数吗？一般地，如果a,b,c是一组勾股数，那么ak,bk,ck（k是正整数）也是一组勾股数吗？
解：（1）3k,4k,5k也是一组勾股数.
因为（3k）2+（4k）2=9k2+16k2=25k2,（5k）2=25k2,
所以（3k）2+（4k）2=（5k）2.
勾股数拓展性质的证明：
（2）如果a,b,c是一组勾股数，那么ak,bk,ck也是一组勾股数.
因为a,b,c是勾股数，则a2+b2=c2
（ak）2+（bk）2=a2k2+b2k2=（a2+b2）k2=c2k2,（ck）2=c2k2
故（ak）2+（bk）2=（ck）2,所以ak,bk,ck也是一组勾股数.
1、如图，四边形ABCD中，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13,求四边形ABCD的面积.
 
三、五种常用辅助线作法
2、有一块地，已知，AD=4m，CD=3m，∠ADC=90°，AB=13m，BC=12m.求这块地的面积.
解：连接AC，∵∠ADC=90°，AD=4，CD=3，∴AC2=AD2+CD2=42+32=25，又∵AC＞0，∴AC=5，又∵BC=12，AB=13，∴AC2+BC2=52+122=169，又∵AB2=169，∴AC2+BC2=AB2，∴∠ACB=90°，∴S四边形ABCD=S△ABC-S△ADC=30-6=24(m2)．
3、如图，是一农民建房时挖地基的平面图，按标准应为长方形，他在挖完后测量了一下，发现ABDC8m，ADBC6m，AC9m，请你运用所学知识帮他检验一下挖的是否合格.
A
D
B
C
解：∵ABDC8，ADBC6， ∴AB2BC28262100 又∵AC29281 ∴AB2BC2AC2 ∴ABC90° ∴该农民挖的不合格.
4、点A是一个圆形森林公园的中心,在森林公园附近有 B 、C 两个村庄,现要在 B、C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得AB=600m,AC=800m,问此公路是否会穿过该森林公园?
1000
600
800
B
C
A
公园半径为400m
影响因素：1.公园的半径2.点A到公路的距离
D
过点A作AD⊥BC交BC于点D.
 
∴这条公路不会穿过自然保护区.
∴AD=480
解：在△ABC中
∵AB2+AC2=6002+8002=10002=BC2.
∴△ABC为直角三角形，∠BAC=90°
∵ 480>400
A
B
C
5、如图，AB=5,AC=3,BC边上的中线AD=2,求△ABC的面积.
解：延长AD并在截取DE=AD,
即△ABC的面积是6.
例2 下面以a,b,c为边长的三角形是不是直角三角形？如果是,那么哪一个角是直角？
(1) a=15 ， b=8 ，c=17;
解：因为152+82=289，172=289，所以152+82=172，根据勾股定理的逆定理，这个三角形是直角三角形，且∠C是直角.
(2) a=13 ， b=14 ， c=15;
解：因为132+142=365，152=225，所以132+142≠152，不符合勾股定理的逆定理，所以这个三角形不是直角三角形.
(3) a:b: c=3:4:5;
解：设a=3k,b=4k,c=5k,因为(3k)2+(4k)2=25k2,(5k)2=25k2,所以(3k)2+(4k)2=(5k)2,根据勾股定理的逆定理，这个三角形是直角三角形，∠C是直角.
变式1： 已知△ABC，AB=n²-1，BC=2n，AC=n²+1(n为大于1的正整数).试问△ABC是直角三角形吗？若是，哪一条边所对的角是直角？请说明理由
解：∵AB²+BC²=(n²-1)²+(2n)² =n4 -2n²+1+4n² =n4 +2n²+1 =(n²+1)² =AC²， ∴△ABC直角三角形，边AC所对的角是直角.
先确定AB、BC、AC、的大小
变式2： 若三角形ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c. 试判断△ABC的形状.
解：∵ a2+b2+c2+50=6a+8b+10c ∴ a2－6a+9+b2－8b+16+c2－10c+25=0. 即 (a－3)²+ (b－4)²+ (c－5)²=0. ∴ a=3, b=4, c=5 即 a2+b2+c2. ∴△ABC直角三角形.
1. 小明想做一个直角三角形的木架，以下四组木棒中，三条能够刚好做成的是（ ）A. 3 cm，4 cm，7 cm B. 6 cm，8 cm，12 cm C. 7 cm，12 cm，15 cm D. 8 cm，15 cm，17 cm
D
课堂练习
2. 在△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，下列结论不正确的是（ ）A. 如果∠A-∠B=∠C，那么△ABC是直角三角形 B. 如果a2=b2-c2，那么△ABC是直角三角形且∠C=90° C. 如果∠A∶∠B∶∠C=1∶3∶2，那么△ABC是直角三角形 D. 如果a2∶b2∶c2=9∶16∶25，那么△ABC是直角三角形
B
3. 在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，且（a+b）（a-b）=c2，则（ ）A. ∠A为直角 B. ∠C为直角C. ∠B为直角 D. 不是直角三角形
A
4. 有四个三角形，分别满足下列条件：①其中一个内角等于另外两个内角之和；②三个内角之比为3∶4∶5；③三边之比为5∶12∶13；④三边长分别为5，24，25. 其中直角三角形有( )A. 1个 B. 2个 C. 3个 D. 4个
B
5.一个三角形的三边长分别是5,12,13，则这个三角形的面积是（ ）A. 30 B. 60 C. 78 D.不能确定6. 一个三角形的三边长的平方分别为32，42，x2，若三角形是直角三角形，则x2的值是( )A. 42 B. 25C. 7 D. 25或7
A
D
证明：设CF=x，则EC=BE=2x，DF=3x，AD=AB=4x.
由勾股定理得：EF2=EC2+FC2=5x2，AE2=AB2+BE2=20x2，AF2=AD2+DF2=25x2，
∴EF2+AE2=25x2=AF2.
由勾股定理的逆定理知，∠AEF=90°.
勾股定理的逆定理
内 容
作用
从三边数量关系判定一个三角形是否是直角形三角形.
如果三角形的三边长a 、b 、c满足a2+b2=c2，那么这个三角形是直角三角形.
注意
最长边不一定是c， ∠C也不一定是直角.
勾股数一定是正整数
课堂小结
谢 谢！