









苏科版八年级上册2.4 线段、角的轴对称性完美版ppt课件
展开2.4.1线段、角的对称性-线段的对称性
一、单选题
1.下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是( )
A.CA=CB,DA=DB B.CA=CB,CD⊥AB
C.CA=DA,CB=DB D.CA=CB,CD平分AB
2.如图,点E,F,G,Q,H在一条直线上,且,我们知道按如图所作的直线为线段的垂直平分线.下列说法正确的是( ).
A.是线段的垂直平分线 B.是线段的垂直平分线
C.是线段的垂直平分线 D.是的垂直平分线
3.如图,在四边形中,垂直平分,垂足为点E,下列结论不一定成立的是( )
A. B. C. D.
4.如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ).
A.在 AC、BC 两边高线的交点处 B.在 AC、BC 两边垂直平分线的交点处
C.在 AC、BC 两边中线的交点处 D.在∠A、∠B两内角平分线的交点处
5.如图,在中,是的垂直平分线,,的周长为,则的周长是( ).
A. B. C. D.
6.如图,,,点在线段的垂直平分线上,若,,则的长为( )
A. B. C. D.
7.如图,等腰△ABC中,AB=AC=3,BC=5,边AC的垂直平分线分别交AC、BC于D、E,则△ABE的周长是( )
A.8 B.9 C.10 D.11
8.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
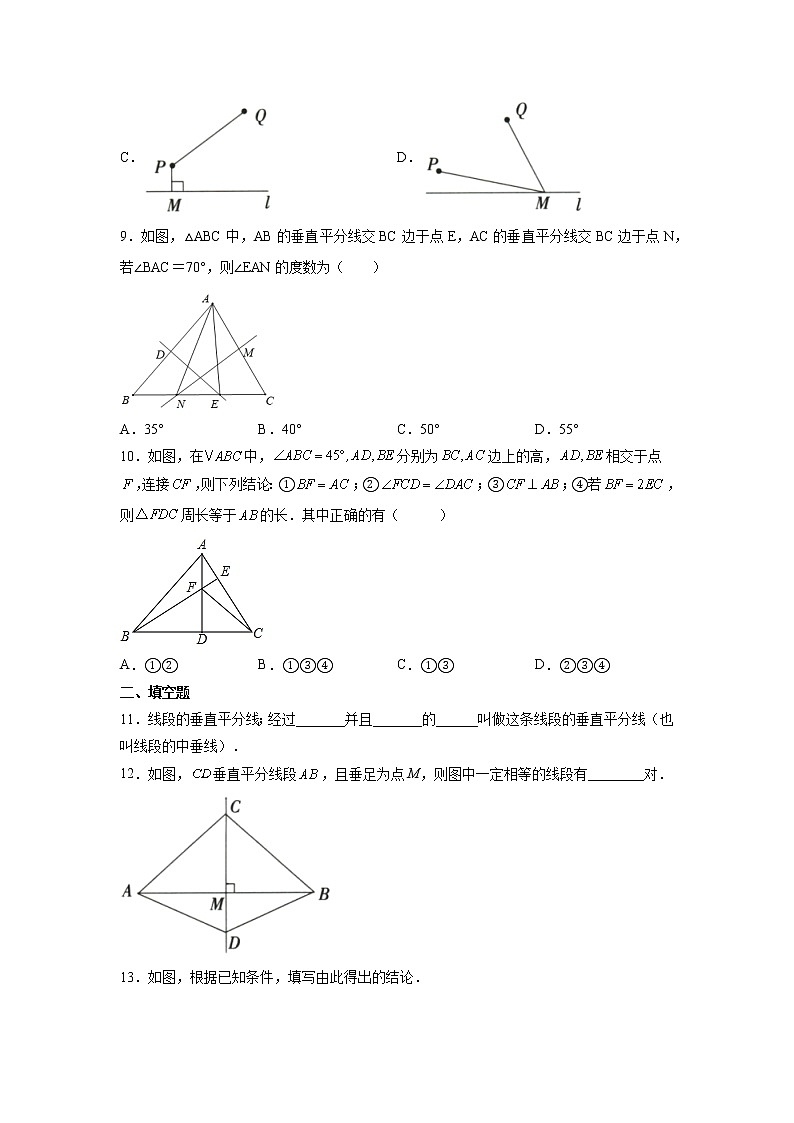
9.如图,△ABC中,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,若∠BAC=70°,则∠EAN的度数为( )
A.35° B.40° C.50° D.55°
10.如图,在中,分别为边上的高,相交于点,连接,则下列结论:①;②;③;④若,则周长等于的长.其中正确的有( )
A.①② B.①③④ C.①③ D.②③④
二、填空题
11.线段的垂直平分线;经过_______并且_______的______叫做这条线段的垂直平分线(也叫线段的中垂线).
12.如图,垂直平分线段,且垂足为点M,则图中一定相等的线段有________对.
13.如图,根据已知条件,填写由此得出的结论.
(1)∵中,,∴_____.
(2)∵中,,∴垂直平分_____.
(3)∵中,,∴_______.
(4)∵中,,∴________.
14.如图,在中,,的垂直平分线交于点D,且的周长为,则________.
15.如图,在△ABC中,AB=AC,∠A=42°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为____度.
16.如图,线段的垂直平分线交于点.若,则__________
17.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,若∠BAC=100°,则∠DAE=_____.
18.如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.
三、解答题
19.如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数?
20.如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)在AD上求作点G,使得GA=GB(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,连接GC,若AG=1,∠BAC=45°,求△BGC的面积.
21.如图所示,在△ABC中,DE是边AB的垂直平分线,交AB于E,交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=50°,求∠DBC的度数.
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为28cm,求BE的长.
22.如图,中,,EF垂直平分,交于点,交于点,且.
(1)若,求的度数;
(2)若周长,,求长.
23.如图,,,,.
(1)求证:;
(2)连接EC,AO,求证:AO垂直平分EC.
24.如图,在中,,AD,BE分别是BC和AC边上的高,AD与BE相交于点F,连接CF.
(1)求证:;
(2)若,,求的周长.
25.如图,在△ABC中,,点为的中点,边的垂直平分线交、、于点、、,连接OA、OB.
(1)求证:△OBC为等腰三角形;
(2)若∠ACF=23°,求的度数.
26.如图,已知AF平分,BC垂直平分AD,垂足为E,点P在CF上,连接PB交线段AF于点M.
(1)求证:;
(2)若,请你判断与之间的数量关系,并说明理由;
(3)在(2)的条件下,当,时,判断是否为等边三角形?并说明理由.
27.如图,在△ABC中,CA=CB,过点A作射线AP∥BC,点M、N分别在边BC、AC上(点M、N不与所在线段端点重合),且BM=AN,连结BN并延长交射线AP于点D,连结MA并延长交AD的垂直平分线于点E,连结ED.
【猜想】如图①,当∠C=30°时,可证△BCN≌△ACM,从而得出∠CBN=∠CAM,进而得出∠BDE的大小为______度.
【探究】如图②,若∠C=β.
(1)求证:△BCN≌△ACM.
(2)∠BDE的大小为______度(用含β的代数式表示).
【应用】如图③,当∠C=120°时,AM平分∠BAC,若AM、BN交于点F,DE=DF,DE=1,则△DEF的面积为______.
苏科版八年级上册2.4 线段、角的轴对称性课文内容课件ppt: 这是一份苏科版八年级上册<a href="/sx/tb_c17044_t3/?tag_id=26" target="_blank">2.4 线段、角的轴对称性课文内容课件ppt</a>,共23页。PPT课件主要包含了几何语言,利用网格线画图,课堂小结,线段的对称性,常用辅助线等内容,欢迎下载使用。
苏科版八年级上册第二章 轴对称图形2.4 线段、角的轴对称性说课课件ppt: 这是一份苏科版八年级上册<a href="/sx/tb_c17044_t3/?tag_id=26" target="_blank">第二章 轴对称图形2.4 线段、角的轴对称性说课课件ppt</a>,共36页。PPT课件主要包含了几何语言,易错提醒,特别解读,解如图所示,特别提醒等内容,欢迎下载使用。
苏科版八年级上册2.4 线段、角的轴对称性优质课件ppt: 这是一份苏科版八年级上册2.4 线段、角的轴对称性优质课件ppt,共60页。PPT课件主要包含了4练习等内容,欢迎下载使用。













