数学苏科版3.2 勾股定理的逆定理教课课件ppt

这是一份数学苏科版3.2 勾股定理的逆定理教课课件ppt，共30页。PPT课件主要包含了学习目标，上节课我们学习了，勾股定理，反过来，都是直角三角形，a2+b2c2，你能证明这个猜想吗，勾股定理的逆定理，符号语言，在△ABC中等内容，欢迎下载使用。

1. 探究并证明勾股定理逆定理，体会“数”与“形”的内在联系；
2. 会应用勾股定理的逆定理判定一个三角形是否是直角三角形；
3. 知道“勾股数”的意义.
直角三角形两直角边的平方和等于斜边的平方.
如果一个三角形的两边平方和等于第三边的平方，那么这个三角形是直角三角形吗？
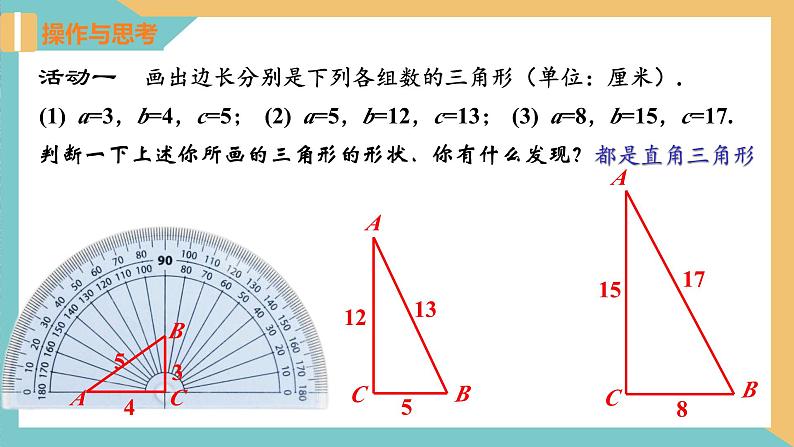
活动一 画出边长分别是下列各组数的三角形（单位：厘米）.
(2) a=5，b=12，c=13；
(3) a=8，b=15，c=17.
(1) a=3，b=4，c=5；
判断一下上述你所画的三角形的形状．你有什么发现？
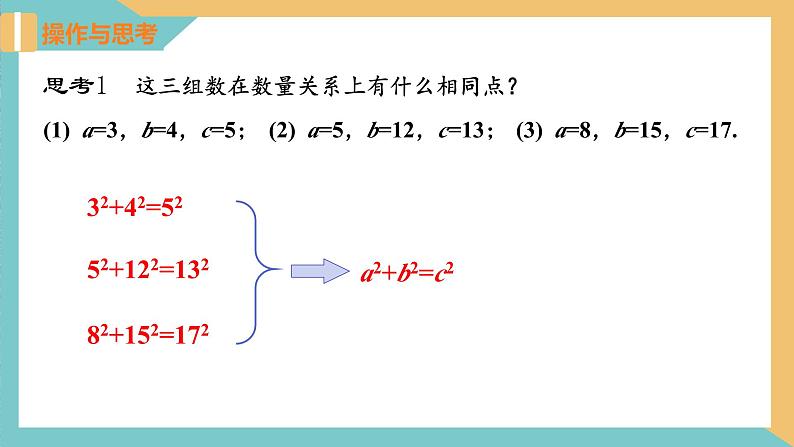
思考1 这三组数在数量关系上有什么相同点？
思考2 根据上述结论你有什么猜想呢？
猜想：如果三角形的三边长a、b、c满足a2+b2=c2，那么这个三角形是直角三角形.
已知：在△ABC中，AB=c , BC=a, CA=b, 且a2+b2=c2.
求证：△ ABC是直角三角形.
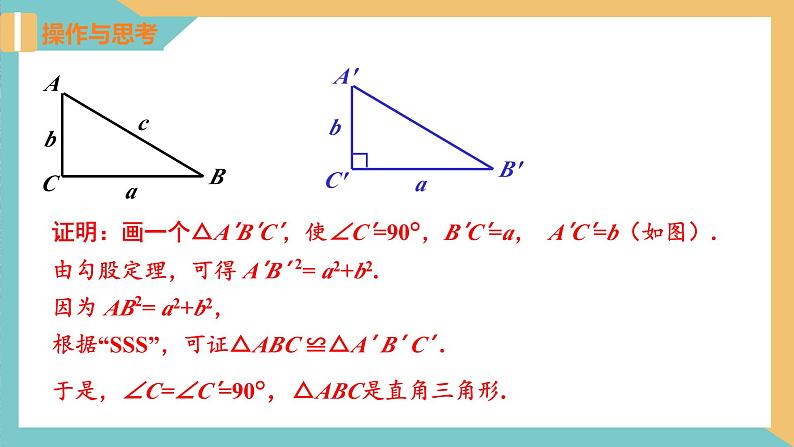
证明：画一个△A′B′C′，使∠C′=90°，B′C′=a， A′C′=b（如图）.
由勾股定理，可得 A′B′ 2= a2+b2.
因为 AB2= a2+b2，
根据“SSS”，可证△ABC ≌△A′ B′ C′ .
于是，∠C=∠C′=90°，△ABC是直角三角形.
如果三角形的三边长a、b、c，且a2 + b2 = c2，那么这个三角形是直角三角形.
∵a²+b²=c²，∴△ABC为直角三角形.
作用：判定一个三角形是否是直角三角形.
这个结论与勾股定理有什么关系呢？
最长边所对应的角为直角，∠C=90°.
勾股定理与其逆定理对比：
在Rt△ABC中，∠C=90°
a2 + b2 = c2
“直角三角形”为条件，数量关系a2 + b2 = c2为结论. 是直角三角形的性质.
都与直角三角形有关，都与三边数量关系a2 + b2 = c2有关
在△ABC中，a2 + b2 = c2
数量关系a2 + b2 = c2为条件，“直角三角形”为结论. 是直角三角形的判定.
(1) a=8，b=15，c=17；
(2) a=13，b=14，c=15.
下面以a、b、c为边长的三角形是不是直角三角形？若是，请指出哪个角是直角.
解：(1) ∵82＋152＝64＋225＝289，172＝289，∴ 82＋152＝172.∴根据勾股定理的逆定理得这个三角形是直角三角形，∠C是直角.
(2) ∵132＋142＝365，152＝225，∴ 132＋142≠152，不符合勾股定理的逆定理，∴ 这个三角形不是直角三角形.
(1) a=7，b=25，c=24；
判断由a、b、c组成的三角形是不是直角三角形，若是，请指出哪个角是直角.
(2) a:b:c=3:4:5.
解：(1) ∵72＋242＝49＋576＝625，252＝625，∴ 72＋242＝252.∴根据勾股定理的逆定理得这个三角形是直角三角形，∠B是直角.
(2)设a=3k、b=4k、c=5k，∵(3k)2+(4k)2=25k2，(5k)2=25k2，∴(3k)2+(4k)2=(5k)2，根据勾股定理的逆定理得这个三角形是直角三角形，∠C是直角.
运用勾股定理的逆定理判断直角三角形的一般步骤：1.找：确定三角形的最长边; 2.算：分别计算出最长边的平方与另两边的平方和; 3.比：通过比较来判断最长边的平方与另两边的平方和是否相等; 4.判：作出结论，若相等，则说明这个三角形是直角三角形，否则不 是直角三角形.
例1 像(3，4，5)、(6，8，10)、(5，12，13)等满足a2＋b2＝c2的三个正整数，通常称为勾股数，请你填表并探索规律．
①从上面2个表中你能发现什么规律？②你能根据发现的规律写出更多的勾股数吗？试试看 ．
解：①规律：一组勾股数，都扩大相同倍数n(n为正整数)，得到一组新数，这组数同样是勾股数.
②答案不唯一，如：15，20，25；13，84，85等．
利用勾股数可以构造直角三角形.
美国哥伦比亚大学图书馆收藏着一块编号为“普林顿322”(plimptn322)的古巴比伦泥板. 泥板上的一些神秘符号揭示了什么奥秘呢？
经过专家的潜心研究，发现其中两列数字竟然是直角三角形的勾和弦的长，只要再添加一列数(如图左边的一列)，那么每行的三个数就是一个直角三角形三边的边长．这些数组都是勾股数组. 人们经过研究发现：勾股数有无数多组.
例2 如图是由边长为1的小正方形组成的网格. (1) 你能判断AD与CD的位置关系吗？说出你的理由. (2) 求四边形ABCD的面积.
∵ AD2=1+4=5，CD2=4+16=20 ，AC= 5
∴ AD2+CD2＝25，AC2＝25
∴ AD2+CD2＝AC2
∴ 由勾股定理的逆定理得：∠CAD＝90°. ∴ AD⊥CD
(2) S四边形ABCD=S△ADC+S△ABC
1. 下列是直角三角形的有（     ）个①△ABC中a²=c²-b²；②△ABC的三内角之比为3：4：7；③ △ABC的三边平方之比为1：2：3；④ 三角形三边之比为3：4：5 A．１　 B．2　　 C．3　　 D．4
用角判断： 1.两个锐角互余 的三角形是直角三角形； 2.有一个角是90°的三角形是直角三角形； 用边判断：如果已知条件与边有关，则可通过勾股定理的逆定理(a²+b²=c²)进行判断.
判断三角形是直角三角形的方法：
判断三个数是不是勾股数的“三步法”:(1)判断三个数是否都为正整数;(2)确定最大数;(3)计算较小两数的平方和是否等于最大数的平方.
3. △ABC的三边长分别是a、b、c，且a＝n2－1，b＝2n，c＝n2＋1．问：△ABC是直角三角形吗？证明你的结论.
解：∵AB²+BC²=(n²-1)²+(2n)² =n4 -2n²+1+4n² =n4 +2n²+1 =(n²+1)² =AC²，∴ 由勾股定理的逆定理得△ABC直角三角形，边AC所对的角是直角.
4.如图，AD⊥BC，垂足为D. 如果CD=1，AD=2，BD=4，那么∠BAC是直角吗？请说明理由.
解：∵AD⊥BC，∴∠ADC=∠ADB=90°.∴ 在Rt△ADC中，AC2=AD2+DC2=22+12=5. 在Rt△ADB中，AB2=AD2+BD2=22+42=20.∵AC2+AB2=20+5=25，BC2=52=25.∴AC2+AB2=BC2.∴△ABC直角三角形，∠BAC=90°.
判定一个三角形为直角三角形
满足a2+b2=c2的三个正整数
注意：最长边不一定是c， ∠C也不一定是直角.
1.下列各数组中，不能作为直角三角形的三边长的是（　 ） A．3，4，5 　 B．10，6，8 C．4，5，6 　 D．12，13，5
2.下列各组数是勾股数的是 （　 ） A. 6，8，10 B. 7，8，9C. 0.3，0.4，0.5 D. 52，122，132
4.如图所示正方形网格中的△ABC，若小方的格边长为1，则△ABC的形状为 （　　）A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 以上答案都不对
5. △ABC的三边分别是a、b、c且满足|a-8 |+(b-6)2=0，则当c2=_______时，△ABC是直角三角形.
4．若一个三角形的三边长满足a2－b2＝c2，则这个三角形一定是 ________三角形．
∴ 根据勾股定理的逆定理得该三角形是直角三角形.
∵152+82＝289，
6．若一个三角形的三边长分别为8 cm，15 cm，17 cm，求该三角形的面积及最长边上的高．
7. 在△ABC中，D为BC边上的点.已知AB=13，AD=12，AC=15，BD=5，求DC的长.
解：∵AB=13，AD=12，BD=5，∴ AB2=AD2+BD2.∴ 由勾股定理的逆定理得：△ABD是直角三角形，且∠ADB=90°.∴∠ADC=90°.在Rt△ADC中，AC2=AD2+DC2. ∵AD=12，AC=15,∴DC2=AC2-AD2=152-122=92.∴ DC=9.
8．观察下列勾股数：3，4，5；5，12，13；7，24，25；9，40，41；…；a，b，c.根据你发现的规律，请写出：(1)当a＝19时，b＝________，c＝________； (2)当a＝2n＋1时，求b，c的值；
解：通过观察知c－b＝1，∵(2n＋1)2＋b2＝c2，∴c2－b2＝(2n＋1)2，(b＋c)(c－b)＝(2n＋1)2，∴b＋c＝(2n＋1)2.又∵c＝b＋1， ∴2b＋1＝(2n＋1)2，∴b＝2n2＋2n，c＝2n2＋2n＋1.