


初中数学北师大版八年级上册3 勾股定理的应用教学ppt课件
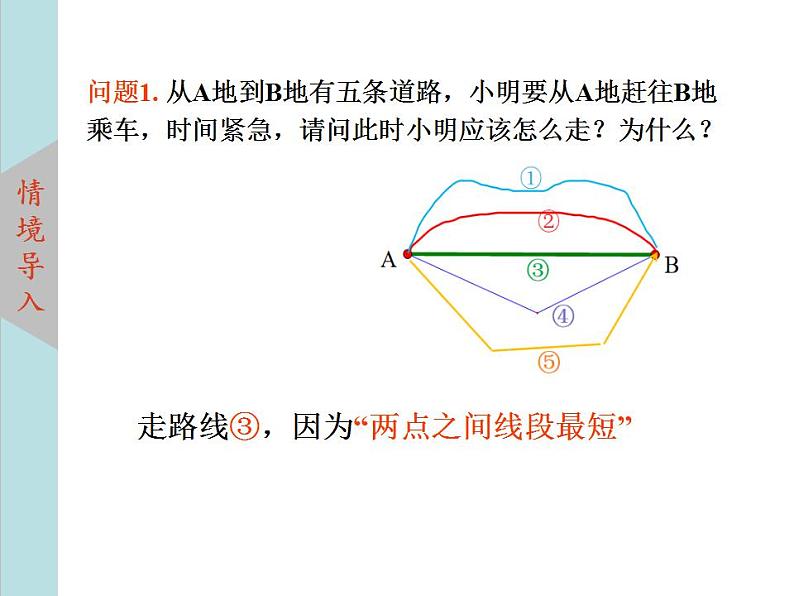
展开问题1. 从A地到B地有五条道路,小明要从A地赶往B地乘车,时间紧急,请问此时小明应该怎么走?为什么?
走路线③,因为“两点之间线段最短”
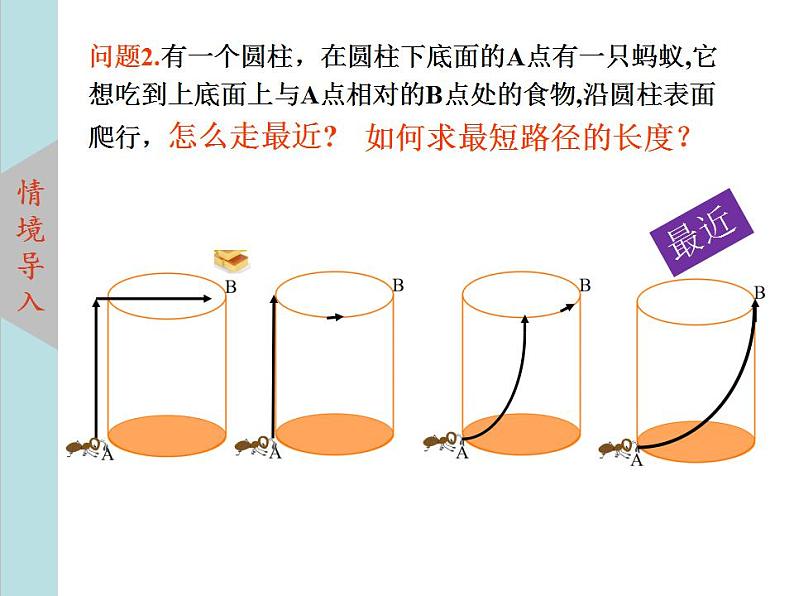
问题2.有一个圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,沿圆柱表面爬行,怎么走最近?
如何求最短路径的长度?
1. 学会运用勾股定理求立体图形中两点之间的最短距离.2. 能够运用勾股定理解决实际生活中的问题.
1.3 勾股定理的应用
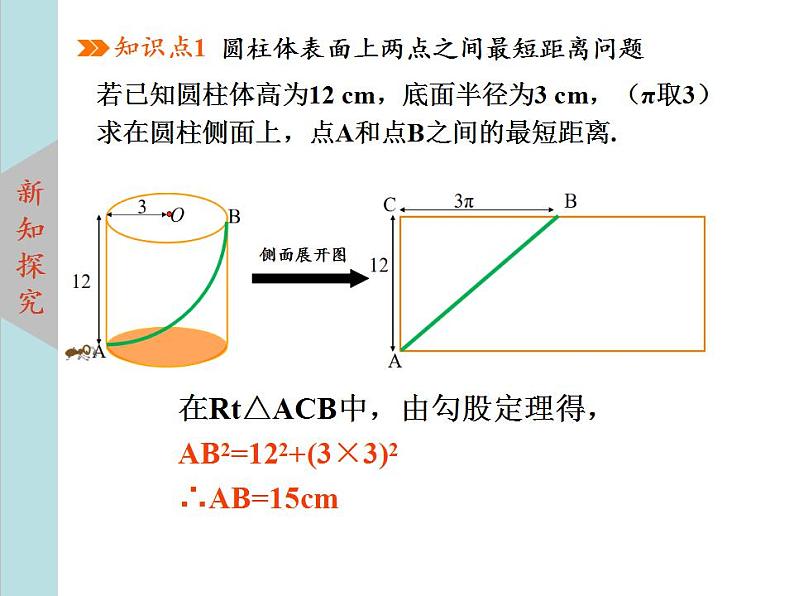
圆柱体表面上两点之间最短距离问题
若已知圆柱体高为12 cm,底面半径为3 cm,(π取3)求在圆柱侧面上,点A和点B之间的最短距离.
在Rt△ACB中,由勾股定理得,AB2=122+(3×3)2∴AB=15cm
例1. 有一只蚂蚁要从一个圆柱形玻璃杯的点A处沿侧面爬到点B处(点A,B均在玻璃杯外部),如图,已知杯子高8 cm,点B距杯口3 cm,杯子底面半径为4 cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)
解:圆柱的侧面展开图为长方形ACDE,如图,其中AC的长为圆柱的底面周长,连接AB,过点B作AE的垂线交AE于点E′,交CD于点D′.
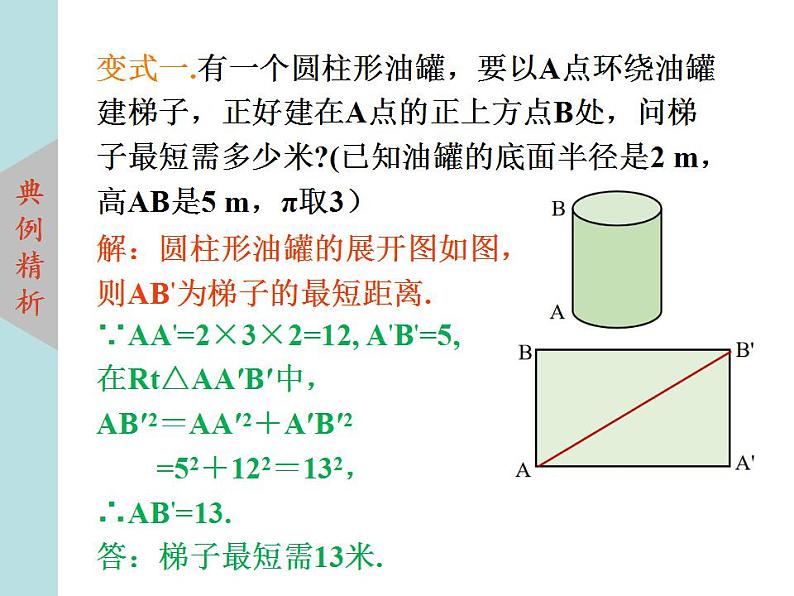
变式一.有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米?(已知油罐的底面半径是2 m,高AB是5 m,π取3)
解:圆柱形油罐的展开图如图,则AB'为梯子的最短距离.
∵AA'=2×3×2=12, A'B'=5,在Rt△AA′B′中,AB′2=AA′2+A′B′2 =52+122=132,∴AB'=13.答:梯子最短需13米.
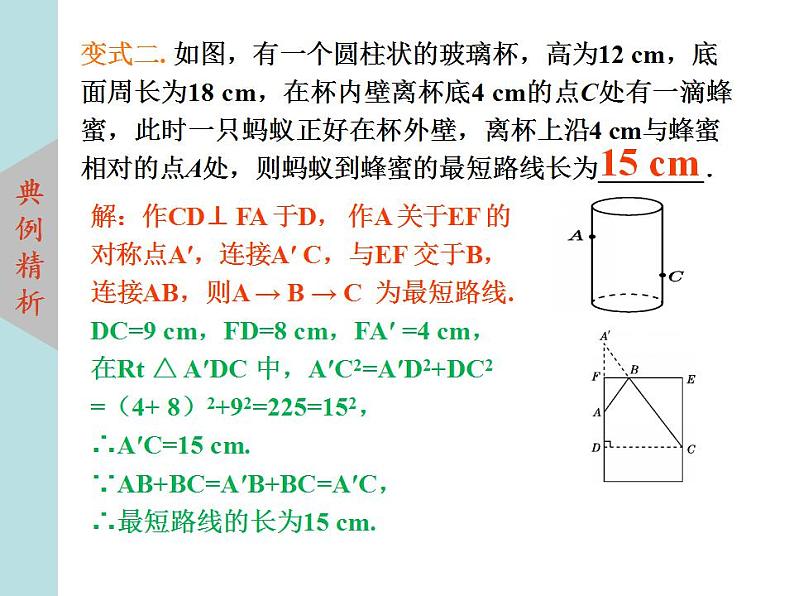
变式二. 如图,有一个圆柱状的玻璃杯,高为12 cm,底面周长为18 cm,在杯内壁离杯底4 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到蜂蜜的最短路线长为________.
解:作CD⊥ FA 于D, 作A 关于EF 的对称点A′,连接A′ C,与EF 交于B,连接AB,则A → B → C 为最短路线.
DC=9 cm,FD=8 cm,FA′ =4 cm, 在Rt △ A′DC 中,A′C2=A′D2+DC2=(4+ 8)2+92=225=152,∴A′C=15 cm. ∵AB+BC=A′B+BC=A′C,∴最短路线的长为15 cm.
长方体表面上两点之间最短距离问题
例2. 长方体的长宽高分别为8cm,6cm,5cm,从A到B,怎么走路径最短.
从顶点A到顶点B最短路径为:AB2=(b+c)2+a2 (a,b,c为长宽高,且a>b,a>c)
例2. 如图,长方体的高为3 cm,底面是正方形,其边长为2 cm.现有一只蚂蚁从A处出发,沿长方体表面到达C处,则蚂蚁爬行的最短路线的长为( )A.4 cm B.5 cm C.6 cm D.7 cm
解析:AC 2= (2+2)2+32=25;∴AC=5cm,∴蚂蚁爬行的最短路线的长为5 cm.
变式. 长方体的长为15 cm,宽为10 cm,高为20 cm,点B离点C的距离是5 cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是 cm?
解析:AB2=202+(10+5)2=625=252,∴AB=25 cm; ∴蚂蚁爬行的最短路线的长为25 cm.
立体图形表面上两点之间最短距离问题
勾股定理及逆定理的实际应用
李叔叔想要检测雕塑(如图)底座正面的边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺.(1)你能替他想办法完成任务吗?(2)李叔叔量得边AD长是30cm,边AB长是40cm,点B,D之间的距离是50cm,边AD垂直于边AB吗?(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验边AD是否垂直于边AB吗?边BC与边AB呢?
解:(2)AD2+AB2=302+402=502=BD2,∴∠DAB=90°,∴AD⊥AB.
(2)李叔叔量得边AD长是30cm,边AB长是40cm,点B,D之间的距离是50cm,边AD垂直于边AB吗?
(3)在AD上取点M,使AM=9,在AB上取点N使AN=12,测量MN是否是15,若是,就是垂直;若不是,就是不垂直.
(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验边AD是否垂直于边AB吗?边BC与边AB呢?
例3. 如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长.
解:设AC=AB=x m,则AE=(x-1)m.
在Rt△ACE中,∠AEC=90°,由勾股定理得AE2+CE2=AC2,即(x-1)2+32=x2,解得, x=5.∴滑道AC的长度为5 m.
1. 如图,一圆柱高8 cm,底面半径为2 cm,一只壁虎从上底面的点A爬到下底面上与点A相对的点B处吃食,它爬行的最短路程(π取3)大约是( )A.20 cm B.14 cm C.10 cm D.无法确定
2. 如图,为了庆祝五一劳动节,学校准备在教学大厅的圆柱形柱子上贴彩带,已知柱子的底面圆周长为1 m,高为3 m.如果要求彩带从柱子底端的A处绕柱子4圈后到达柱子顶端的B处(线段AB与地面垂直),那么应购买彩带的长至少为( )A.2 mB.3 mC.4 mD.5 m
3. 如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),则最短路线长为 .
4. 如图,长方体的长为9,宽为4,高为12,点B与点C的距离为1,一只蚂蚁如果要沿长方体的侧面从点A爬行到点B,需要爬行的最短距离是( )A.12 B.13 C.15 D.17
5. 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是;有一个水池,水面是一个边长为10尺的正方形,在水池中央有一根新生的芦苇,它高出水面1尺。如果把这根芦苇垂直拉到岸边,它的顶端恰好到达岸边的水面。请问这个水池的深度和这根芦苇的长度各是多少?
解:如图,设AB =x尺,则BC =( x +1)尺,根据勾股定理得:x2+52=(x+1)2,即:(x+1)2-x2 =52,解得, x=12, ∴芦苇长为12+1=13(尺),答:水深为12尺,芦苇长为13尺.
1. 利用勾股定理解决立体图形表面上两点之间最短距离问题
2. 利用勾股定理及逆定理解决实际应用问题
北师大版八年级上册3 勾股定理的应用教课课件ppt: 这是一份北师大版八年级上册3 勾股定理的应用教课课件ppt,共14页。PPT课件主要包含了知识回顾,a2+b2c2,△ABC是直角三角形,学习目标,课堂导入,新知探究,AB2122+92,AB15厘米,课堂练习,x+1等内容,欢迎下载使用。
初中北师大版3 勾股定理的应用评优课ppt课件: 这是一份初中北师大版3 勾股定理的应用评优课ppt课件,共35页。PPT课件主要包含了导入新知,素养目标,探究新知,蚂蚁A→B的路线,数学思想,立体图形,平面图形,巩固练习,牛奶盒,长方体爬行路径等内容,欢迎下载使用。
初中数学北师大版八年级上册3 勾股定理的应用课堂教学ppt课件: 这是一份初中数学北师大版八年级上册3 勾股定理的应用课堂教学ppt课件,共27页。PPT课件主要包含了学习目标,蚂蚁A→B的路线,数学思想,立体图形,平面图形,牛奶盒,△ABC为直角三角形,解得x5,实际问题,数学问题等内容,欢迎下载使用。













