






八年级上册1 认识无理数教学课件ppt
展开1. 感受非有理数存在的必要性和合理性;2. 能判断一个数是否为非有理数.
2.1 认识无理数第1课时 不是有理数的数
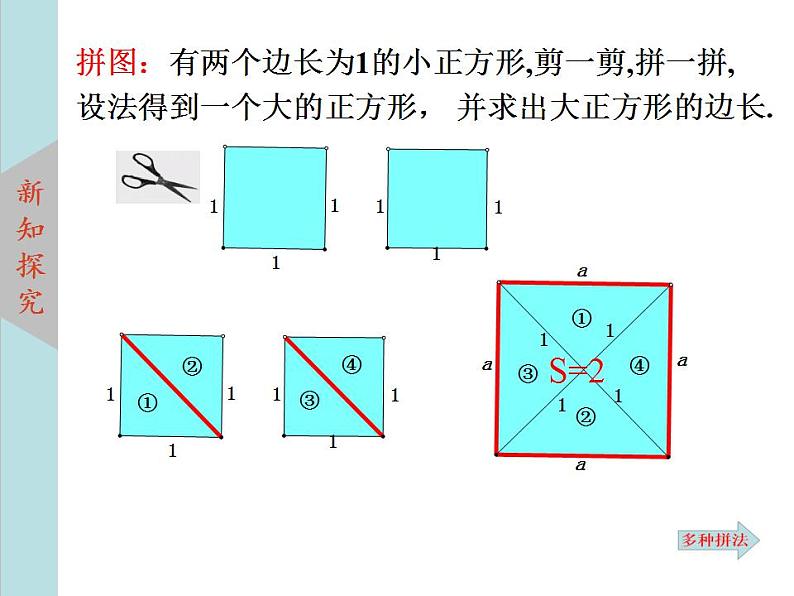
拼图:有两个边长为1的小正方形,剪一剪,拼一拼,设法得到一个大的正方形, 并求出大正方形的边长.
问题:(1)设大正方形的边长为a,a满足什么条件?
(2)a可能是整数吗?
(3)a可能是分数吗?
12=1,22=4,32=9,…
两个相同的最简分数的乘积仍然是分数
事实上,我们可以证明,在a2=2中,a既不是整数,也不是分数,所以a不是有理数.
做一做: (1)如图,以直角三角形的斜边为边 的正方形的面积是多少?
(2)设该正方形的边长为b,b满足什么 条件?
根据勾股定理,得12+22=5,所以正方形的面积是5.
因为22=4,32=9,4<5<9,所以b不可能是整数;没有两个相同的分数相乘得5,所以b不可能是分数;因为没有一个整数或分数的平方为5,所以b不是有理数.
在上面两个问题中,即a2=2,b²=5中,数a,b确实存在,但都不是有理数.
利用面积和勾股定理发现非有理数
例1. 如图,正三角形的边长为2,高为h,h是有理数吗?
解:∵△ABC时正三角形,AD⊥BC∴BD=CD=1在Rt△ABD中,h2=22-12=3
∵1
例2. 在直角三角形ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.(1)计算:①当a=1,c=2时,b2= ; ②当a=3,c=5时,b2= ; ③当a=0.6,c=1时,b2= .
1. 下图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段.试分别找出两条长度是有理数的线段和两条长度不是有理数的线段.
解:由勾股定理知,线段AB,DE,AE的长能用有理数表示;
线段AC,CE,B的长不能用有理数表示.
2. 请你在如图所示的方格纸上按照如下要求设计直角三角形.(1)使它的三边中有一边边长不是有理数;(2)使它的三边中有两边边长不是有理数;(3)使它的三边边长不是有理数.
3.满足下列条件的数不是有理数的是( )A. 2a +5=8 B. a2= D.2a2=18
4. 两直角边分别是3和5的直角三角形的斜边长是( ) A. 整数 B. 分数 C. 有理数 D.非有理数
5. 如果方程x2=m 的解是有理数,则数m不能取下列四个数中的( ) A. 1 B. 4 C. 0.25 D.0.5
6.下列正方形的边长不是有理数的是( ) A. 面积为2.56的正方形 B.面积为36的正方形 C.面积为 的正方形 D.面积为10的正方形
7.一个长方形的长与宽分别是6,3,它的对角线的长可能 ( ) A.是整数B.是分数C.是有理数D.既不是整数,也不是分数
8.如图,在△ABC中,CD⊥AB,垂足为D,AC=6,AD=5,问:CD可能是整数吗?可能是分数吗?可能是有理数吗?
解:在Rt△ACD中,由勾股定理得,CD2=AC2-AD2=62-52=1111不能写成一个整数的平方,所以CD不可能是整数.因为最简分数的平方仍是分数,所以CD不可能是分数.所以CD不可能是有理数.
1. 非有理数的存在在生活中确实存在既不是整数也不是分数的数,既不是有理数的数.例如在a2=2,b²=5中,数a,b不是有理数.2. 识别非有理数有理数包括:整数和分数.如果一个数既不是整数也不是分数,那么这个数不是有理数.
初中1 认识无理数精品课件ppt: 这是一份初中1 认识无理数精品课件ppt,共25页。PPT课件主要包含了思考导入,有理数如何分类,有理数,导入新知,素养目标,无理数的概念,探究新知,想一想,解330,巩固练习等内容,欢迎下载使用。
八年级上册1 认识无理数一等奖ppt课件: 这是一份八年级上册1 认识无理数一等奖ppt课件,共24页。PPT课件主要包含了导入新知,素养目标,剪一剪拼一拼,利用拼图发现非有理数,探究新知,方法一,方法二,a22,探究二,巩固练习等内容,欢迎下载使用。
初中数学北师大版八年级上册1 认识无理数教学课件ppt: 这是一份初中数学北师大版八年级上册1 认识无理数教学课件ppt,共18页。PPT课件主要包含了学习目标,复习巩固,0负整数,负分数,无理数的发现,a是有理数吗,典型例题,随堂练习,不可能,不是整数也不是分数等内容,欢迎下载使用。













