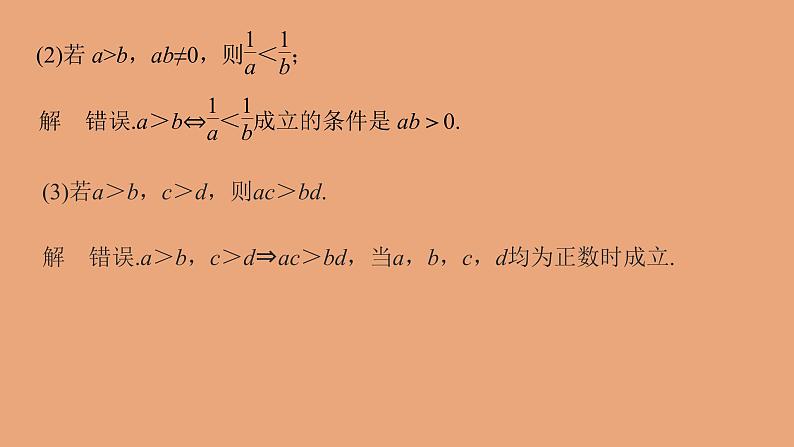
人教B版 (2019)必修 第一册2.2.1 不等式及其性质教学ppt课件

这是一份人教B版 (2019)必修 第一册2.2.1 不等式及其性质教学ppt课件，共25页。PPT课件主要包含了题型探究，答案3，又∵e＜0，易错点，解析∵ab0等内容，欢迎下载使用。
知识点一　不等式的常用性质1.如果a>b，则bb，b>c，则a>c.3.如果a>b，则a＋c>b＋c.4.如果a>b，c>0，则ac>bc.
知识点二　不等式的主要性质1.如果a>b，c>d，则a＋c>b＋d.2.如果a>b>0，c>d>0，则ac>bd.3.如果a>b>0，则an>bn(n∈N＋).
思考　在不等式的性质中、没有除法公式，那么你怎样理解在不等式性质中的除法运算？
答　除去一个不为零的数，即乘上这个数的倒数.
题型一　利用不等式性质判断命题的真假例1　判断下列不等式关系是否正确，并说明理由.
解　正确.∵c2≠0且c2＞0，
(3)若a＞b，c＞d，则ac＞bd.
解　错误.a＞b，c＞d⇒ac＞bd，当a，b，c，d均为正数时成立.
∴可组成3个正确命题.
证明　∵c＜d＜0，∴－c＞－d＞0，又∵a＞b＞0，∴a＋(－c)＞b＋(－d)＞0，即a－c＞b－d＞0，
跟踪训练2　已知a＞b，m＞n，p＞0，求证：n－ap＜m－bp.
证明　∵a＞b，又p＞0，∴ap＞bp.∴－ap＜－bp，又m＞n，即n＜m.∴n－ap＜m－bp.
解　∵3