初中21.5 反比例函数教学演示课件ppt

这是一份初中21.5 反比例函数教学演示课件ppt，共26页。PPT课件主要包含了学习目标及重难点，课程导入，描点连线，课程讲授，新课推进，解列表如下，x增大，y减小，y增大，曲线特点等内容，欢迎下载使用。

1. 经历画反比例函数的图象、归纳得到反比例函数的图象特征和性质的过程 ；2. 了解和掌握反比例函数的图象和性质；(重点) 3. 能够初步应用反比例函数的图象和性质解题. (难点)
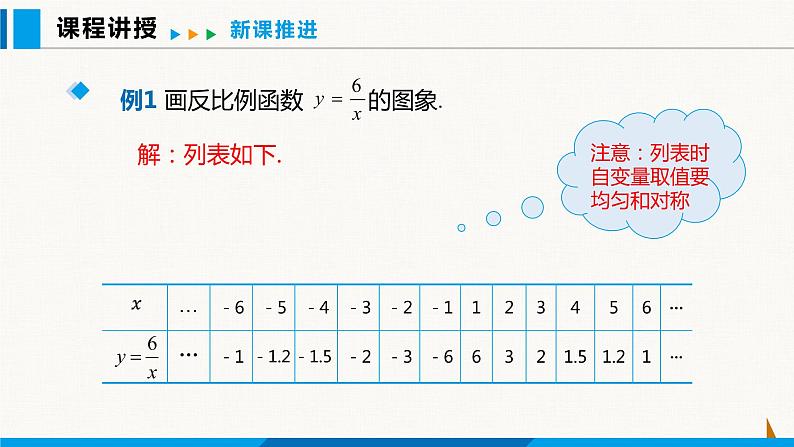
1. 我们学习一次函数和二次函数时，研究了函数的哪些内容?是如何进行研究的?
我们研究了函数的表达式、图象、性质，根据表达式，通过列表、描点、连线画出函数图象，从图象的形状、位置、增减性等多个方面分析归纳函数的性质.
2.画函数图象的一般方法和步骤是怎样的?
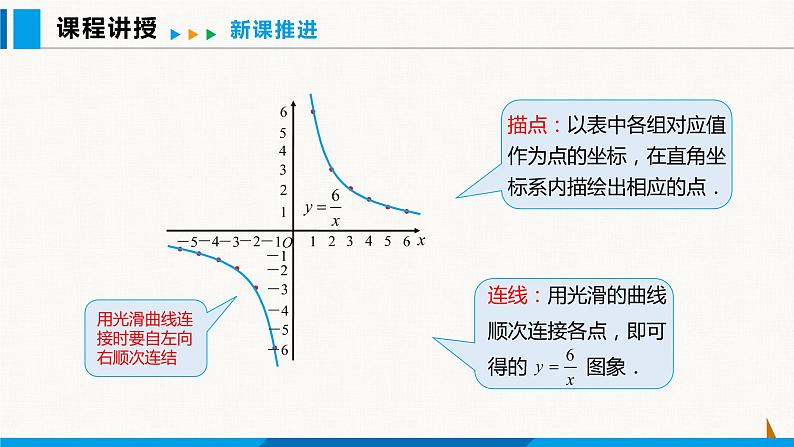
观察这个函数图象，回答问题：
(1) 每个函数图象分别位于哪些象限？
(2) 在每一个象限内，随着x的增大，y 如何变化？你能由它们的表达式说明理由吗？
2、“在每个象限内”该怎么理解？
如 在每个象限内递减，但是在整个定义域不是递减的（x<0时，y<0,x>0,y>0;开始小于0，后来大于0，显然不是递减）
(1) 双曲线的两个分支与x轴和y轴没有交点； (2) 双曲线的两个分支关于原点成中心对称．
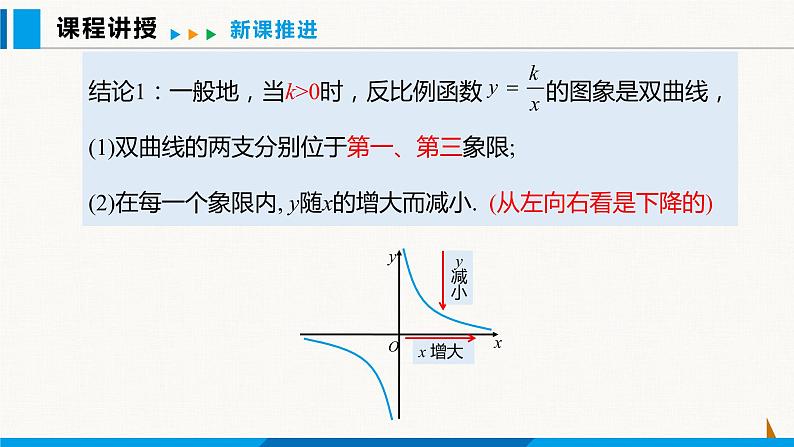
(1) 当 k > 0 时，双曲线的两支分别位于第一、三 象限，在每一象限内，y 随 x 的增大而减小；
(2) 当 k < 0 时，双曲线的两支分别位于第二、四 象限，在每一象限内，y 随 x 的增大而增大.
P (2，2) Q (4，1)
猜想S1，S2与k的关系
2、若在反比例函数 中也 用同样的方法分别取 P，Q 两点，填写表格：
由前面的探究过程，可以猜想：
∴ S矩形 AOBP=PB·PA=－a·b=－ab=－k；
若点 P 在第二象限，则 a<0，b>0，
若点 P 在第四象限，则 a>0，b<0，
∴ S矩形 AOBP=PB·PA=a· (－b)=－ab=－k.
综上，S矩形 AOBP=|k|.
A. SA >SB>SC B. SA1. 如图，在函数 (x＞0)的图象上有三点A，B ， C，过这三点分别向 x 轴、y 轴作垂线，过每一点所作的两条垂线与x轴、 y轴围成的矩形的面积分别为SA ，SB，SC，则 ( )
2. 如图，过反比例函数 图象上的一点 P，作 PA⊥x 轴于A. 若△POA 的面积为 6，则 k = .
提示：当反比例函数图象在第二、四象限时，注意 k＜0.
3. 若点 P 是反比例函数图象上的一点，过点 P 分别向 x 轴、y 轴作垂线，垂足分别为点 M，N，若四边形 PMON 的面积为 3，则这个反比例函数的关系式是 .
1、 已知反比例函数 ，y 随 x 的增大而增大，求a的值.
解：由题意得 a2+a－7=－1，且a－1<0． 解得 a=－3.
已知反比例函数 的图象过点(－2，－3)，函数图象上有两点 A( ，y1)，B(5，y2)，则 y1与y2的大小关系为 ( )
如图，P，C是函数 (x>0) 图象上的任意两点，过点 P 作 x 轴的垂线 PA，垂足为 A，过点 C 作 x 轴的垂线 CD，垂足为 D，连接 OC交 PA 于点 E. 设 △POA 的面积为 S1，则 S1= ；梯形CEAD的面积为 S2，则 S1 与 S2 的大小关系是 S1 S2；△POE 的面积 S3 和 S2 的大小关系是S2 S3.