初中数学沪科版九年级上册21.5 反比例函数精品ppt课件

这是一份初中数学沪科版九年级上册21.5 反比例函数精品ppt课件，共23页。PPT课件主要包含了新知导入，抛物线，描点法，新知讲解，解1列表，2描点，Px0y0，第一和第三象限，关于原点成中心对称，课堂练习等内容，欢迎下载使用。

1、反比例函数的一般形式是什么？
2、自变量x的取值范围是什么？
一次函数有 ，它们的图象是一条 。二次函数有 ，它们的图象是一条 。反比例函数有 ，
(1)、(4)、(6)
(3)、(7)、(8)
反比例函数的图象又会是什么样子的呢？
同学们还记得作函数图象的方法吗？
描点法作函数图象的一般步骤：
怎样用描点法画出函数 的图象呢？
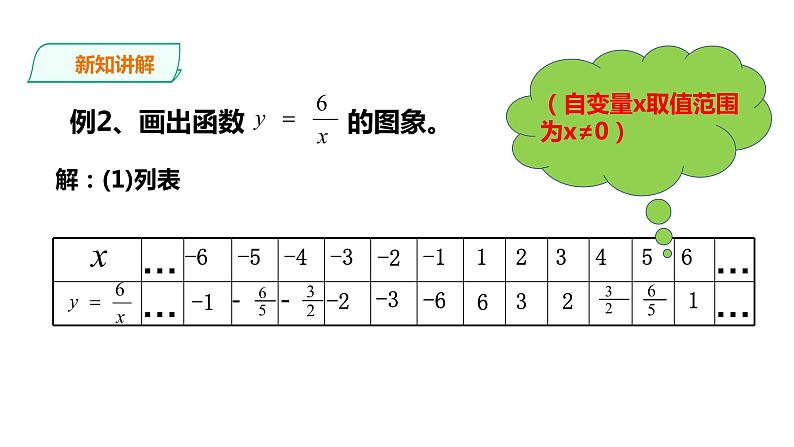
例2、画出函数 的图象。
（自变量x取值范围为x≠0）
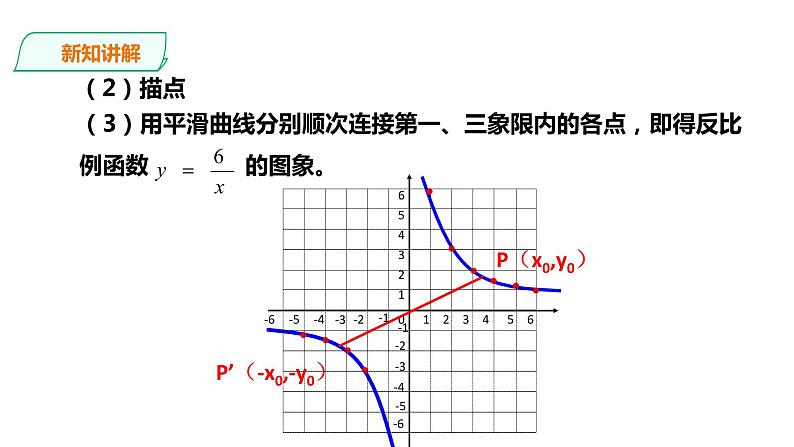
（3）用平滑曲线分别顺次连接第一、三象限内的各点，即得反比例函数 的图象。
P’（-x0,-y0）
活动探究一：观察反比例函数 的图象，回答下列问题。（小组讨论，3min）
1、函数图象有几个分支？分别位于哪几个象限内？
2、在每个象限内, 图象自左向右是上升还是下降？函数y的值随着x值的增大会怎样变化？
3、两条曲线会与x轴、y轴相交吗？为什么？
4、从对称性角度观察，函数图象是轴对称图形吗？是中心对称图形吗？
1、函数图象有几个分支？ 分别位于哪几个象限内？
函数y随x的增大而减小
4、从对称性角度观察，函数图象是轴对称图形吗？是中心对称图形吗？
无限接近x轴和y轴，但永远不与它们相交
是轴对称图形，对称轴是一三象限或二四象限的角平分线；
观察可知：（1）因为自变量x≠0，所以y轴把函数 的图象分隔成两个分支，它们分别在第一和第三象限内。 (2)在每个象限内，图象自左向右下降，函数y随x的增大而减小，图象的两个分支都可以无限延伸，并无限接近x轴和y轴，但永远不与它们相交。（3）如果点P（x0,y0）在函数 的图象上，那么点P’（-x0,-y0）也应在它的图象上。
注意：①列表时自变量取值要均匀和对称②x≠0③选整数较好计算和描点。
画出反比例函数 的图象，并比较 和 图像的特点。
2、当k>0时,图象的两个分支分别在哪些象限内，在每个象限内，y随x怎样变化？
3、当k<0时,图象的两个分支分别在哪些象限内，在每个象限内，y随x怎样变化？
1、这两个函数图象有什么共同特征？有什么不同之处？
反比例函数的图象和性质：
函数图象的两个分支分别位于第一、三象限
在每个象限内，图象自左向右下降
在每个象限内，函数y随x的增大而减小
函数图象的两个分支分别位于第二、四象限
在每个象限内，图象自左向右上升
在每个象限内，函数y随x的增大而增大
例3.已知反比例函数 （1）如果这个函数图象经过点（-3,5），求k的值。（2）如果这个函数图象在它所处的象限内，函数y随x的增大而减小，求k的范围。
解：（1）因为函数图象经过点（-3,5），代入函数的表达式，得解方程，得k=-7(2)根据题意，有2k-1>0解不等式 ，得k>
变式1、如图所示，当k＜0时，反比例函数 和一次函数y=kx+2的图像大致是图( )
解：∵k=4>0 ∴图象在第一、三象限内，每一象限内y随x的增大而减小 ∵x10, ∴点A(-2,y1)，点B(-1,y2)在第三象限点C(3,y3)在第一象限。∴y3>0, y2 如图，过点C（1,2）分别作x轴、y轴的平行线，交直线y=－x+6于A、B两点，若反比例函数 （x＞0）的图像与ABC有公共点，则k的取值范围是（ ）A．2≤k≤9 B. 2≤k≤8 C. 2≤k≤5 D. 5≤k≤8
分析：由题意可得点A、B 的坐标分别为A(4，2) ，B(1，5) ，当反比例函数过点C 时，K=1×2=2 ，若反比例函数与直线AB 有交点D，设点 D的坐标为 (x,-x+6)，则 ,-x+6 = ，所以K=-x2+6x=-(x-3) 2+9，所以 K的最大值为9 ，所以 2≤k≤9。
这节课你有哪些收获？我们一 起来分享一下吧！
1、反比例函数的图像： 双曲线
当k＜0时，图象的两个分支分别位于第二、四象限，在每个象限内，图象自左向右上升，函数y随x的增大而增大。
当k＞0时，图象的两个分支分别位于第一、三象限，在每个象限内，图象自左向右下降，函数y随x的增大而减小;
21.5.2 反比例函数
1、反比例函数图像2、反比例函数性质