




沪科版九年级上册21.5 反比例函数完美版ppt课件
展开1.会用描点法画出反比例函数;(重点)2.掌握反比例函数图象的特征; (重点)3.理解并掌握反比例函数的性质.(难点)
1.什么是反比例函数?
2.反比例函数的定义中需要注意什么?
(1)k 是非零常数.
一般地,表达式形如 y = ( k是常数, k ≠0 )的函数叫做反比例函数.
3.还记得一次函数的图象与性质吗?
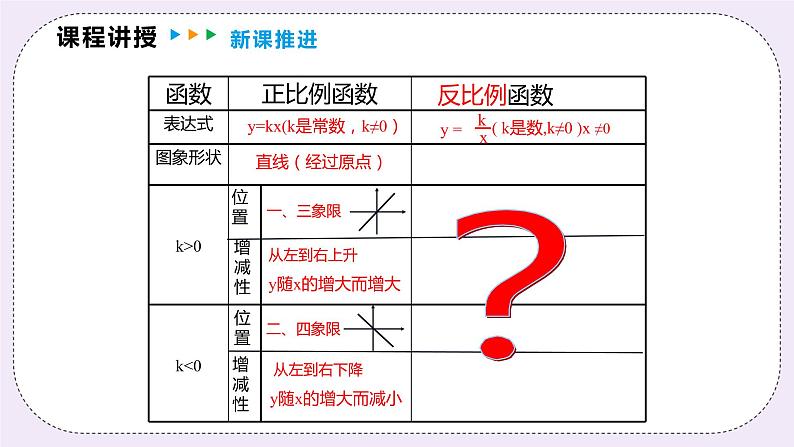
y=kx(k是常数,k≠0)
从左到右上升y随x的增大而增大
从左到右下降y随x的增大而减小
4.如何画函数的图象?
想一想: 正比例函数y=kx (k≠0)的图象的位置和增减性是由谁决定的?我们是如何探究得到的?
反比例函数的图象与性质又如何呢?
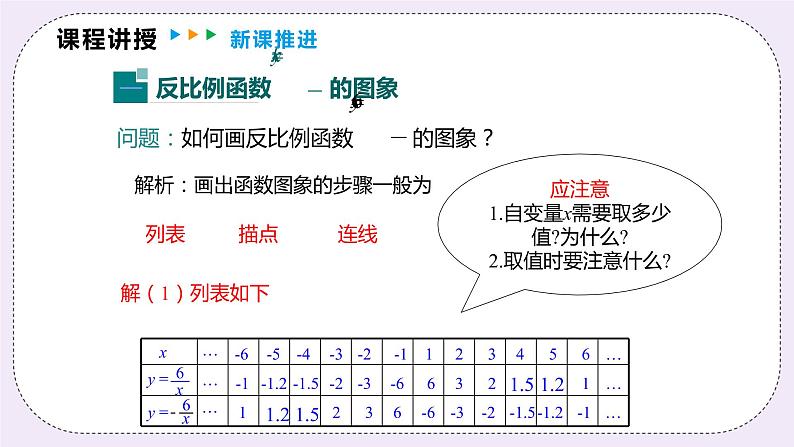
解析:画出函数图象的步骤一般为
应注意1.自变量x需要取多少值?为什么?2.取值时要注意什么?
(2)根据表中x,y的数值在平面直角坐标系中描点(x,y);
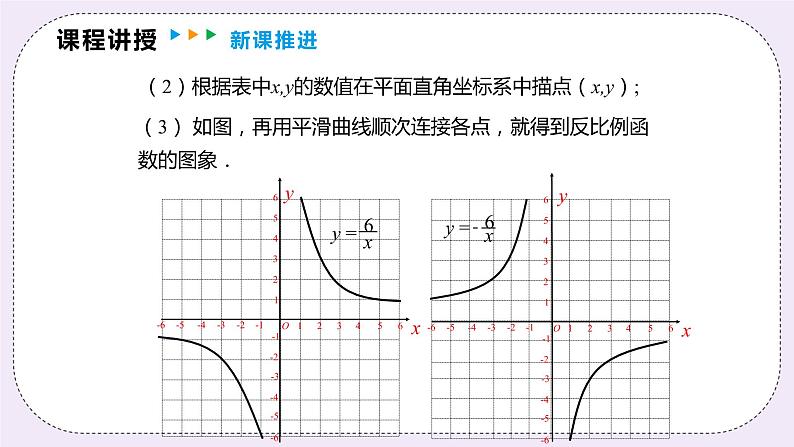
(3) 如图,再用平滑曲线顺次连接各点,就得到反比例函数的图象.
想一想:你认为作反比例函数图象时应注意哪些问题?
1.列表时,自变量的值可以选取一些互为相反数的值这样既可简化计算,又便于对称性描点;2.列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;3.连线时,一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;……
(1)观察 和 的图象,它们有什么相同点和不同点?
轴对称图形,也是以原点为对称中心的中心对称图形.
相同点:1. 两支曲线构成; 2. 与坐标轴不相交; 3.图象自身关于原点成中心对称; 4.图象自身是轴对称图形.不同点: 的图象在第一、三象限; 的图象在第二、四象限.
形状: 反比例函数 的图象由两支曲线组成,因此称 反比例函数 的图象为双曲线. 位置:由k决定: 当k>0时,两支曲线分别位于_______________内; 当k<0时,两支曲线分别位于_______________内.
例1:若双曲线y = 的两个分支分别在第二、四象限,则 k 的取值范围是( )A. k>B. k<C. k=D.不存在解析:反比例函数图象的两个分支分别在第二、四象限,则必有2k-1<0,解得k< .故选B.
例2:如图所示的曲线是函数 (m为常数)图象的一支.(1)求常数m的取值范围;(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的表达式.
解:(1)由题意可得,m-5>0,解得m>5.
问题:观察下列的函数图象,填一填.
(2)函数图象分别位于哪几个象限?
(1)上面三个函数相应的k值分别是________,则k___0.
x<0时,图象在第二象限;x>0 时,图象在第四象限.
(4)在每个象限内,曲线从左往右______,所以随着x值的增大,y的值怎样变化?
(3)当x取什么值时,图象在第二象限?当x取什么值时,图象在第四象限?
当k>0时,在每个象限内,y随x的增大而减小;
当k<0时,在每个象限内,y随x的增大而增大.
例3:已知反比例函数y = .(1)如果这个函数图象经过点(-3,5),求k的值.(2)如果这个函数图象在它所处的象限内,函数y随x的增大而减小,求k的范围.
解:(1)因为函数图象经过点(-3,5),代入函数表达式, 得 解得, k= -7. (2)根据题意,有 2k-1>0, 解不等式,得
例4:已知反比例函数 的图象过点(-2,-3),函数图象上有三点A( ),B(5,y2) ,C(-8,y3) ,则y1,y2,y3的大小关系为 ( )A.y1> y2 > y3 B.y1< y2 < y3C.y2 > y1 >y3 D.不能确定
解析:已知反比例函数过点(-2,-3),所以可知k > 0 ,可判断 y1>0, y2 > 0, y3 < 0. 由概念可知,当k >0时,在每个象限内,y随x的增大而减小,所以y2>y1>0>y3.
已知两点( , ),( , )在函数 的图象上,当 > >0时,下列结论正确的是 ( ) A. > >0 B. < <0 C. > >0 D. < <0
1.在反比例函数 的图象上分别取点P,Q向x轴、y轴作垂线,围成面积分别为S1,S2的矩形,填写表格:
2.若在反比例函数 中也用同样的方法分别取P,Q两点,填写表格:
由前面的探究过程,可以猜想:
我们就k<0的情况给出证明:
设点P的坐标为(a,b)
∴S矩形 AOBP=PB·PA=-a·b=-ab=-k;
若点P在第二象限,则a<0,b>0
若点P在第四象限,则a>0,b<0
∴S矩形 AOBP=PB·PA=a·(-b)=-ab=-k.
综上,S矩形 AOBP=|k|.
自己尝试证明k>0的情况.
点Q是其图象上的任意一点,作QA垂直于y轴,作QB垂直于x轴,矩形AOBQ的面积与k的关系是S矩形 AOBQ= 推理:△QAO与△QBO的面积和k的关系是S△QAO=S△QBO=
对于反比例函数 ,
反比例函数的面积不变性
例5:如图,过反比例函数 图象上的一点P,作PA⊥x轴于点A.若△POA的面积为6,则k= .
当k>0时,两支曲线分别位于第一、三象限内
当k<0时,两支曲线分别位于第二、四象限内
描点法:列表、描点、连线
反比例函数图象中比例系数k的几何意义
当k>0时,在每一象限内,y的值随x的增大而减小.
当k<0时,在每一象限内,y的值随x的增大而增大.
2.函数 的图象,在每一象限内 y随x的增大而_____.
3.在双曲线 的一支上, y随x的增大而减小,则m的取值范围是 ____ .
A.SA >SB>SC B.SA
数学沪科版21.5 反比例函数备课ppt课件: 这是一份数学沪科版21.5 反比例函数备课ppt课件,共22页。PPT课件主要包含了旧知回顾,反比例函数图象和性质,解列表,k<1,回答下面的问题等内容,欢迎下载使用。
初中数学沪科版九年级上册第23章 解直角三角形23.1 锐角的三角函数精品课件ppt: 这是一份初中数学沪科版九年级上册第23章 解直角三角形23.1 锐角的三角函数精品课件ppt,共30页。PPT课件主要包含了学习目标及重难点,课程导入,课程讲授,探索1正切的定义,问题1,问题2,问题3,定义中的几点说明,完成下列填空,随堂小练习等内容,欢迎下载使用。
初中22.1 比例线段完美版ppt课件: 这是一份初中22.1 比例线段完美版ppt课件,共22页。PPT课件主要包含了学习目标及重难点,课程导入,课程讲授,图形的放大,图形的缩小,两个图形相似,正六边形,对应边成比例,课堂练习,ABDF等内容,欢迎下载使用。













