初中数学人教版八年级下册16.1 二次根式一课一练

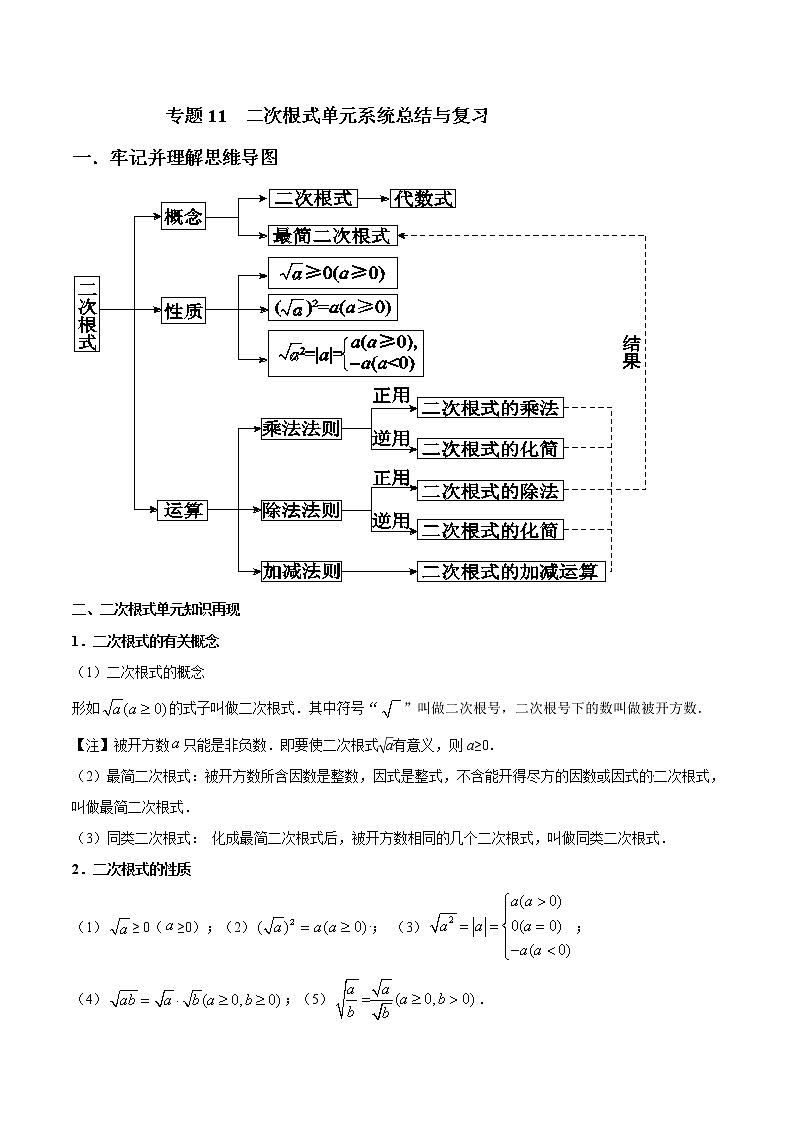
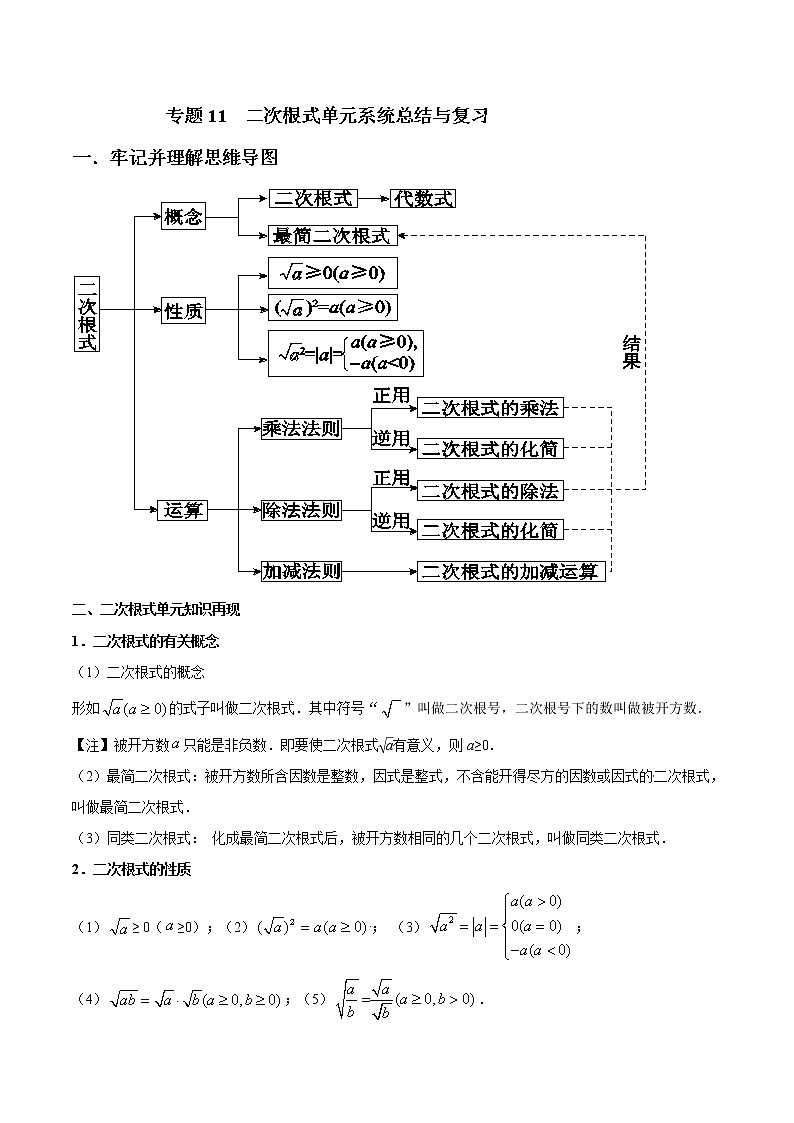
专题11  二次根式单元系统总结与复习

一．牢记并理解思维导图

二、二次根式单元知识再现

1．二次根式的有关概念

（1）二次根式的概念

形如的式子叫做二次根式．其中符号“”叫做二次根号，二次根号下的数叫做被开方数．

【注】被开方数只能是非负数．即要使二次根式有意义，则a≥0．

（2）最简二次根式：被开方数所含因数是整数，因式是整式，不含能开得尽方的因数或因式的二次根式，叫做最简二次根式．

（3）同类二次根式： 化成最简二次根式后，被开方数相同的几个二次根式，叫做同类二次根式．

2．二次根式的性质

（1）≥ 0（≥0）；（2）； （3）；

（4）；（5）．

3．二次根式的运算

（1）二次根式的加减

合并同类二次根式：在二次根式的加减运算中，把几个二次根式化为最简二次根式后，若有同类二次根式，可把同类二次根式合并成一个二次根式．

（2）二次根式的乘除

乘法法则：；除法法则：．

（3）二次根式的混合运算

二次根式的混合运算顺序与实数的运算顺序一样，先乘方，后乘除，最后加减，有括号的先算括号内的．

在运算过程中，乘法公式和有理数的运算律在二次根式的运算中仍然适用．

三、单元考点例题解析

考点一：   二次根式的相关概念有意义的条件

求二次根式中字母的取值范围的基本依据：

（1）开方数大于或等于零；

（2）分母中有字母时，要保证分母不为零.

【例题1】（2021湖北襄阳）若二次根式在实数范围内有意义，则x的取值范围是（　　）

A．x≥﹣3 B．x≥3 C．x≤﹣3 D．x＞﹣3

【答案】A

【解析】根据二次根式的概念，形如（a≥0）的式子叫做二次根式，进而得出答案．

若二次根式在实数范围内有意义，

则x+3≥0，

解得：x≥﹣3．

【例题2】（2021湖南怀化）函数y＝的自变量x的取值范围是 　     　．

【答案】x≥2且x≠3．

【解析】让二次根式的被开方数为非负数，分式的分母不为0列不等式组求解集即可．

由题意得：，

解得：x≥2且x≠3．

【例题3】用※定义一种新运算：对于任意实数m和n，规定，如：．

（1）求；

（2）若，求m的取值范围，并在所给的数轴上表示出解集．

【答案】(1)；(2)，图见解析

【解析】（1）根据新定义规定的运算法则列式，再由有理数的运算法则计算可得；
（2）根据新定义列出关于x的不等式，解不等式即可得．

解：（1）=

=

=

（2）∵，
∴

解得：

将解集表示在数轴上如下：

考点二：   二次根式的性质

初中阶段主要涉及三种非负数：   ≥ 0，|a|≥0，a2≥0.如果若干个非负数的和为0，那么这若干个非负数都必为0.这是求一个方程中含有多个未知数的有效方法之一.

【例题4】（2021重庆）下列计算中，正确的是（　　）

A．5﹣2＝21 B．2+＝2 C．×＝3 D．÷＝3

【答案】C

【解析】根据合并同类二次根式法则、同类二次根式的定义、二次根式的乘法和除法法则逐一判断即可．

A．5﹣2＝3，此选项计算错误；

B．2与不是同类二次根式，不能合并，此选项计算错误；

C．×＝××＝3，此选项计算正确；

D．÷＝＝，此选项计算错误．

考点三：   二次根式的运算及应用

二次根式的混合运算的运算顺序与整式的运算顺序一样，先算乘方，再算乘除，最后算加减，有括号的先算括号内的，在具体运算中可灵活运用运算律和乘法公式简化运算.

【例题5】计算：

 ＋

【答案】见解析。

【解析】先把各个二次根式化简，然后合并同类二次根式即可．

(3)原式＝＋(×2 －3×)

＝4 －2 ＋－

＝3 －.

【例题6】阅读材料：

小明在学习二次根式的化简后，遇到了这样一个需要化简的式子：．该如何化简呢？思考后，他发现3+2＝1+2+（）2＝（1+）2．于是＝＝1+．善于思考的小明继续深入探索；当a+b＝（m+n）2时（其中a，b，m，n均为正整数），则a+b＝m2+2mn+2n2．此时，a＝m2+2n2，b＝2mn，于是，＝m+n．请你仿照小明的方法探索并解决下列何题：

（1）设a，b，m，n均为正整数且＝m+n，用含m，n的式子分别表示a，b时，结果a＝　       　，b＝　        　；

（2）利用（1）中的结论，选择一组正整数填空：＝　　+　　；

（3）化简：．

【分析】（1）利用已知直接去括号进而得出a，b的值；

（2）取m＝2，n＝1，计算a和b的值，利用完全平方公式，变形得出答案；

（3）直接利用完全平方公式，变形化简即可．

【解答】解：（1）由题意得：a+b＝（m+n）2，

∴a+b＝m2+3n2+2mn，

∴a＝m2+3n2，b＝2mn；

故答案为：m2+3n2；2mn；

（2）取m＝2，n＝1，则a＝m2+3n2＝7，b＝2mn＝4，

7+4＝（2+）2；

故答案为：；

（3）＝＝+1．

考点四：  二次根式的化简求值

【例题7】（2021山东泰安）（1）先化简，再求值：，其中a＝+3；

【答案】见解析。

【解析】（1）分式的混合运算，注意先算乘除，然后算加减，有小括号先算小括号里面的，然后代入求值；

解：（1）原式＝[]

＝

＝﹣，

当a＝+3时，原式＝﹣；

考点五： 本章解题思想方法

1.分类讨论思想

【例题8】

2.整体思想

【例题9】

3.类比思想 

【例题10】阅读材料：

小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+=（1+）2．善于思考的小明进行了以下探索：

设a+b=（m+n）2（其中a、b、m、n均为整数），则有a+b=m2+2n2+2mn．

∴a=m2+2n2，b=2mn．这样小明就找到了一种把类似a+b的式子化为平方式的方法．

请你仿照小明的方法探索并解决下列问题：

（1）当a、b、m、n均为正整数时，若a+b=，用含m、n的式子分别表示a、b，得：a=　    　，b=　  　；

（2）利用所探索的结论，找一组正整数a、b、m、n填空：　　+2=（　　+）2；

（3）若a+4=，且a、m、n均为正整数，求a的值？

【答案】（1）m2+3n2，2mn．

（2）4、1．

（3）13

【解析】根据完全平方公式运算法则，即可得出a、b的表达式；首先确定好m、n的正整数值，然后根据（1）的结论即可求出a、b的值；根据题意，4=2mn，首先确定m、n的值，通过分析m=2，n=1或者m=1，n=2，然后即可确定好a的值．

（1）∵a+b=，

∴a+b=m2+3n2+2mn，

∴a=m2+3n2，b=2mn．

（2）设m=1，n=1，

∴a=m2+3n2=4，b=2mn=2．

故答案为4、2、1、1．

（3）由题意，得：

a=m2+3n2，b=2mn

∵4=2mn，且m、n为正整数，

∴m=2，n=1或者m=1，n=2，

∴a=22+3×12=7，或a=12+3×22=13．