资料中包含下列文件,点击文件名可预览资料内容










当前文件暂不支持在线预览,请下载使用
还剩16页未读,
继续阅读
成套系列资料,整套一键下载
- 人教版数学八年级下册 16.1.2 《二次根式的性质与化简》课件+教学设计+导学案+分层练习(含答案解析) 课件 1 次下载
- 人教版数学八年级下册 16.2.1 《二次根式的乘法》课件+教学设计+导学案+分层练习(含答案解析) 课件 1 次下载
- 人教版数学八年级下册 16.2.2 《二次根式的除法》课件+教学设计+导学案+分层练习(含答案解析) 课件 2 次下载
- 人教版数学八年级下册 16.3.1 《二次根式的加减》课件+教学设计+导学案+分层练习(含答案解析) 课件 2 次下载
- 人教版数学八年级下册 16.3.2 《二次根式的混合运算》课件+教学设计+导学案+分层练习(含答案解析) 课件 1 次下载
人教版数学八年级下册 16.1.1 《二次根式的概念》课件+教学设计+导学案+分层练习(含答案解析)
展开
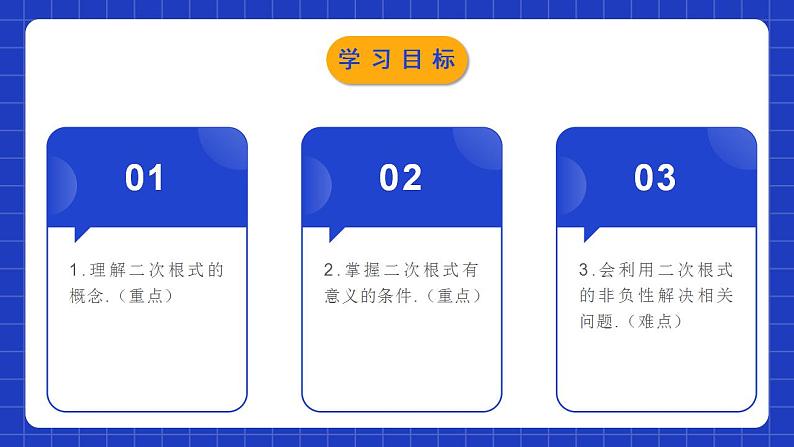
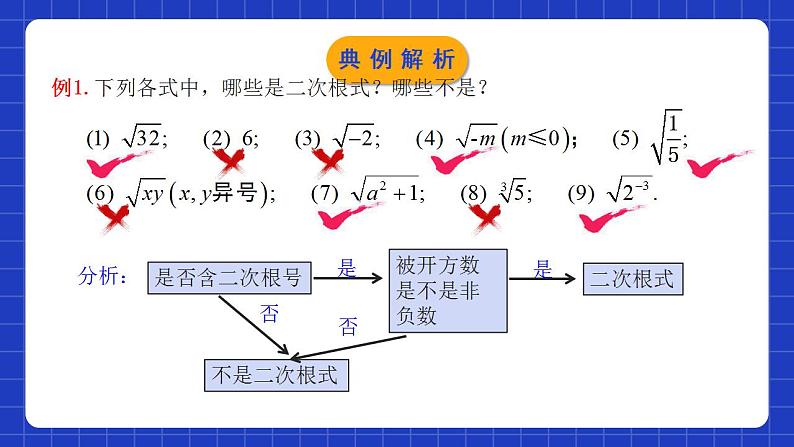
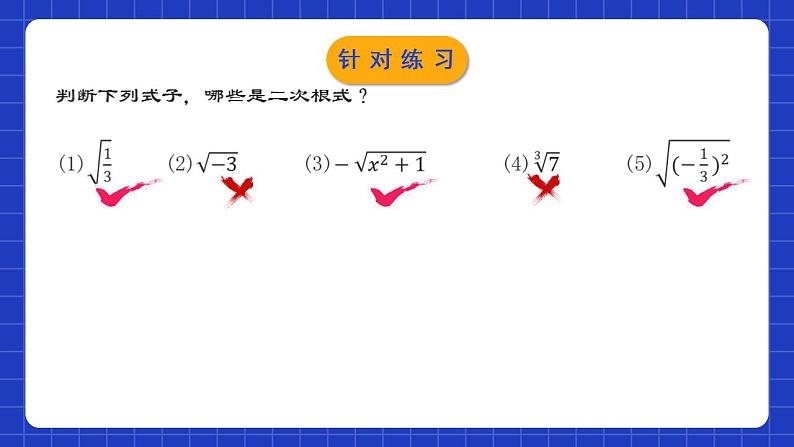
二次根式的概念学习目标0102031.理解二次根式的概念.(重点)2.掌握二次根式有意义的条件.(重点)3.会利用二次根式的非负性解决相关问题.(难点) 1.什么叫做一个数的平方根?如何表示? 2.什么是一个数的算术平方根?如何表示?复习回顾3.(1)16的平方根是什么?算术平方根是什么?(2)0的平方根是什么?算术平方根是什么?(3)-7有没有平方根?有没有算术平方根?复习回顾 用带有根号的式子填空,看看写出的结果有什么特点:(1)面积为3的正方形的边长为____,面积为S的正方形的边长为____.(2)一个长方形的围栏,长是宽的2倍,面积为130m2,则它的宽为_____m.(3)一个物体从高处自由落下,落到地面所用的时间t(单位:s)与开始落下时离地面的高度h(单位:m)满足关系h=5t2.如果用含有h的式子表示t,则t=_____.知识精讲1.表示a的算术平方根;2.a可以是数,也可以是式;3.形式上含有二次根号 ;4.a≥0, ≥0 (双重非负性);5.既可表示开方运算,也可表示运算的结果.知识精讲例1.下列各式中,哪些是二次根式?哪些不是?是否含二次根号被开方数是不是非负数二次根式不是二次根式是是否否分析:典例解析 针对练习解:由x-2≥0,得x≥2.典例解析(2)∵被开方数需大于或等于零,∴3+x≥0,∴x≥-3.∵分母不能等于零,∴x-1≠0,∴x≠1.∴x≥-3 且x≠1.【点睛】要使二次根式在实数范围内有意义,即需满足被开方数≥0,列不等式求解即可.若二次根式为分母或二次根式为分式的分母时,应同时考虑分母不为零.当x是怎样的实数时,下列各式在实数范围内有意义?解(1)由题意得x-1>0,∴x>1.针对练习1.单个二次根式如 有意义的条件:2.多个二次根式相加如 有意义的条件:3.二次根式作为分式的分母如 或 有意义的条件:4.二次根式与分式的和如 或 有意义的条件:A≥0A>0A≥0且B≠0总结提升二次根式的双重非负性知识精讲解:因为由题意可知a-2=0,b-3=0,c-4=0,解得a=2,b=3,c=4.所以a-b+c=2-3+4=3.【点睛】多个非负数的和为零,则可得每个非负数均为零.初中阶段学过的非负数主要有绝对值、偶次幂及二次根式.典例解析已知|3x-y-1|和 互为相反数,求x+4y的平方根.解:由题意得3x-y-1=0且2x+y-4=0.解得x=1,y=2.∴x+4y=1+2×4=9,∴x+4y的平方根为±3.针对练习解:由题意得 ∴x=3,y=8,∴3x+2y=25.∵25的算术平方根为5,∴3x+2y的算术平方根为5.【点睛】若 ,则根据被开方数大于等于0,可得a=0.典例解析解:由题意得∴a=3,∴b=4.当a为腰长时,三角形的周长为3+3+4=10;当b为腰长时,三角形的周长为4+4+3=11.针对练习 AB达标检测3.使得 有意义的x值有( )A.0个 B.1个 C.无数个 D.以上都不对4.使式子 有意义的x的取值范围在数轴上表示为( )AB达标检测 CD达标检测 x≥46152021达标检测11.要画一个面积为18cm2的长方形,使它的长与宽之比为3:2,它的长、宽各应取多少? 达标检测 达标检测1.表示a的算术平方根;2.a可以是数,也可以是式;3.形式上含有二次根号 ;4.a≥0, ≥0 (双重非负性);5.既可表示开方运算,也可表示运算的结果.小结梳理课程结束
相关资料
更多









