





初中19.2.2 一次函数图片ppt课件
展开1.若正比例函数y=kx(k≠0)经过点(-1,2),则该正比例函数的解析式为y=___________.2.如图,一次函数y=ax+b的图象经过A、B两点,则关于x的不等式ax+b<0的解集是 . 3. 一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的解析式可以是 .(任写出一个符合题意即可)
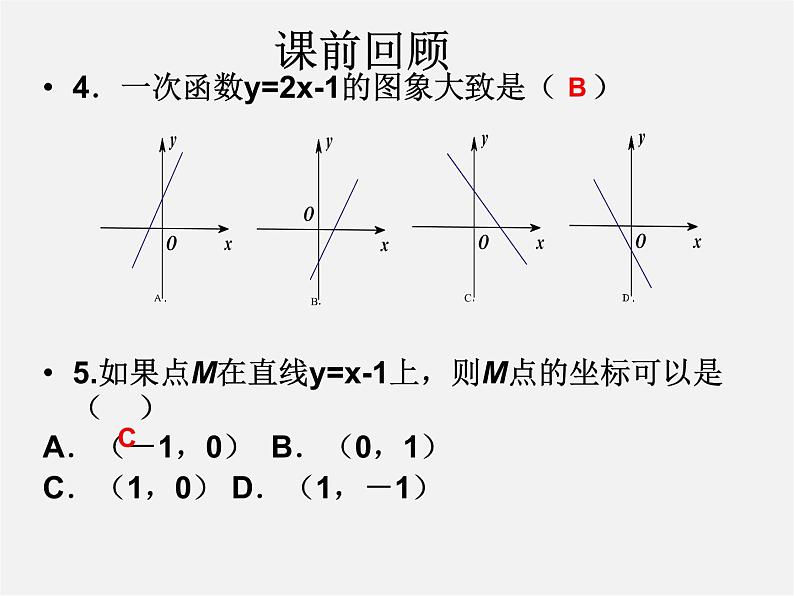
4.一次函数y=2x-1的图象大致是( )5.如果点M在直线y=x-1上,则M点的坐标可以是( )A.(-1,0) B.(0,1) C.(1,0) D.(1,-1)
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
思 考
y=k xn +b为一次函数的条件是什么?
一 次 函 数
正 比 例 函 数
y = k x ( k≠0 ) y=k x + b(k,b为常数,且k ≠0)
k>0 k<0 k>0 k<0
k>0时,在Ⅰ, Ⅲ象限;k<0时,在Ⅱ, Ⅳ象限.正比例函数是特殊的一次函数
k>0,b>0时在Ⅰ, Ⅱ,Ⅲ象限;k>0,b<0时在Ⅰ, Ⅲ, Ⅳ 象限k<0, b>0时,在Ⅰ,Ⅱ, Ⅳ象限.k<0, b<0时,在Ⅱ, Ⅲ, Ⅳ象限平行于 y = k x ,可由它平移而得
当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.
一、基础问题 填空题:(1) 有下列函数:① , ② y=5x ,③ , ④ 。其中过原点的直线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象过第一、二、三象限的是_____。
(2)、如果一次函数y=kx-3k+6的图象经过原点,那么k的值为________。 (3)、已知y-1与x成正比例,且x=-2时,y=4,那么y与x之间的函数关系式为_________________。
方法:待定系数法:①设;②代;③解;④还原
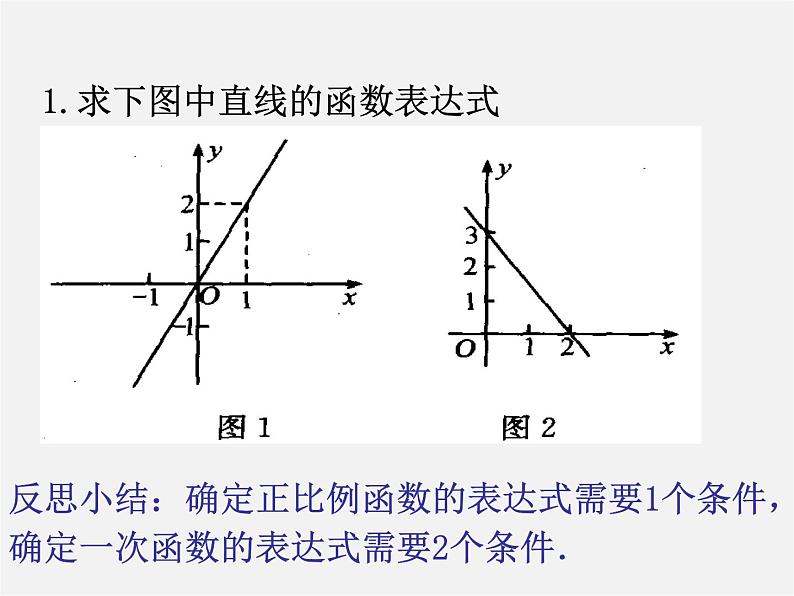
1.求下图中直线的函数表达式
反思小结:确定正比例函数的表达式需要1个条件,确定一次函数的表达式需要2个条件.
2、已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
例3、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式。
4、 小明根据某个一次函数关系式填写了下表:
其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。
(北京)如图,直线y=2x+3与x轴交于点A,与y轴交于点B. (1)求A,B两点的坐标; (2)过点B作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积
如图,在平面直角坐标系中,直线l:y=-4/3x+4分别交x轴、y轴于点A, B,将△AOB绕点 顺时针旋转90°后得到△A`OB` (1)求直线A'B'的解析式; (2)若直线A'B'与直线l相交于点C,求△A'BC的面积
(2013•河北)如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒. (1)当t=3时,求l的解析式; (2)若点M,N位于l的异侧,确定t的取值范围; (3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点. (1)求k的值; (2)若点P是第二象限内的直线上的一个动点,当点P运动过程中,试写出三角形OPA的面积S与x的函数关系式,并写出自变量x的取值范围; (3)探究:当P运动到什么位置时,三角形OPA的面积为 27/8 ,并说明理由.
已知:如图,平面直角坐标系xOy中,A(1,0),B(0,1),C(-1,0),过点C的直线绕点C旋转,交y轴于点D,交线段AB于点E. (1)求∠OAB的度数及直线Az的解析式; (2)若△OCD与△BDE的面积相等, ①求直线CE的解析式; ②若y轴上的一点P满足∠APE=45°,请你直接写出P点的坐标.
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA=8,OC=6.(1)求直线MN的解析式;(2)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
17.如图,已知直线l:y= x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 .
(2012•东营)在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2( 7/2 , 3/ 2),那么点An的纵坐标是 ________.
在直角坐标系中,正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…、AnBnCnCn﹣1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上,点C1、C2、C3、…、Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点A n的坐标为 _________ ,Bn的坐标是 _________ .
2.一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是( )
1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( ) (A) (B) (C) (D)
二、图像辨析
3.直线y1=kx与直线y2=kx-k在同一坐标系内的大致图象是( )
.1、柴油机在工作时油箱中的余油量Q(千克)与工作时间t(小时)成一次函数关系,当工作开始时油箱中有油40千克,工作3.5小时后,油箱中余油22.5千克(1)写出余油量Q与时间t的函数关系式;(2)画出这个函数的图象。
点评:画函数图象时,应根据函数自变量的取值范围来确定图象的范围,比如此题中,因为自变量0≤t≤8,所以图像是一条线段。
三、能力提升1
2.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。(1)服药后____时,血液中含药量最高,达到每毫升_______毫克。(2)服药5时,血液中含药量为每毫升____毫克。(3)当x≤2时,y与x之间的函数关系式是_____。(4)当x≥2时,y与x之间的函数关系式是_________。(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是___ 小时。.
点评(1)根据图像反映的信息解答有关问题时,首先要弄清楚两坐标轴的实际意义,抓住几个关键点来解决问题;(2)特别注意,第5问中由y=3对应的x值有两个;(3)根据函数图像反映的信息来解答有关问题,比较形象、直观,从中能进一步感受“数形结合思想”。
3.如图,矩形ABCD中,AB=6,动点P以2个单位/s速度沿图甲的边框按B→C→D→A的路径移动,相应的△ABP的面积s关于时间t的函数图象如图乙.根据下图回答问题:
(1)P点在整个的移动过程中△ABP的面积是怎样变化的?
(3)图乙中的a在图甲中具有什么实际意义?a的值是多少?
(2)图甲中BC的长是多少?
解:(1) P点在整个的移动过程中△ABP的面积先逐渐从0增大到30,然后在3分钟内保持30不变,再从30逐渐减小;(2)BC=10; (3)a=30. a的值表示点P在CD边上运动时, △ABP的面积;
点评:此类动点问题中,应根据点P的不同运动路线,找出对应的函数图像以及每段图像对应的自变量取值范围,抓住几个关键点,并理解函数图像中横、纵坐标的实际意义。
6、如图所示,反映了某公司产品的销售收入与销售量的关系。反映了该公司产品的销售成本与销售量的关系,根据图意填空:(1)l对应的表达式是 ,对应的表达式是 。( 2)当销售量为2吨时,销售收入= 元,销售成本= 元。(3)当销售量为6吨时,销售收入= 元,销售成本= 元。(4)当销售量等于 时,销售收入等于销售成本。(5)当销售量 时,该公司盈利(收入大于成本)。当销售 时,该公司亏损(收入小于成本)。
1.下列函数中,不是一次函数的是 ( )
2.如图,正比例函数图像经过点A,该函数解析式是______
4.点P(a,b)点Q(c,d)是一次函数y=-4x+3图像上的两个点,且a
1.一次函数 y 1=kx+b与y 2=x+a的图像如图所示,则下列结论(1)k<0;(2)a>0;(3)当x<3时,y 1
3.一个函数图像过点(-1,2),且y随x增大而减少,则这个函数的解析式是___
4.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是_________.
1、直线y=2x+1与y=3x-1的交点P的坐标为____,点P到x轴的距离为_______,点P到y轴的距离为______。
2.一次函数的图象过点(0,3) ,且与两坐标轴围成的三角形面积为 9/4,一次函数的解析式为_________________。
3.如图,将直线OA向上平移1个单位,得到一个一次函数的图像,那么这个一次函数的解析式是____________________
如图,在平面直角坐标系中,点A的坐标是(4,0),点P在直线y=-x+m上,且AP=OP=4,求m的值。
如图1,在矩形中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MRN的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( ) A.N处 B.P处 C.Q处 D.M处
一个一次函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,-3a)与点(a,-6),求这个函数的解析式。
若函数y=kx+b的图象平行于y= -2x的图象且经过点(0,4), 则直线y=kx+b与两坐标轴围成的三角形的面积是:
解:∵y=kx+b图象与y= - 2x图象平行 ∴k=-2
∵图像经过点(0,4)∴b=4
∴此函数的解析式为y= - 2x+4
∵函数y= - 2x+4与两坐标轴的交点为(0,4) (2,0)
∴S△= ×2 ×4=4
初中人教版19.2.2 一次函数复习课件ppt: 这是一份初中人教版19.2.2 一次函数复习课件ppt,共14页。PPT课件主要包含了一次函数,过原点的直线,ykxk≠0,K>0,k<0,一二三,一三四,一二四,二三四,K>0b>0等内容,欢迎下载使用。
数学八年级下册19.2.2 一次函数教学ppt课件: 这是一份数学八年级下册19.2.2 一次函数教学ppt课件,共1页。
人教版19.2.2 一次函数课堂教学课件ppt: 这是一份人教版19.2.2 一次函数课堂教学课件ppt,共13页。PPT课件主要包含了一次函数一,小试身手,y025x+6,≤x≤10,挑战自我,cm25cm,h25h,回顾与反思,勤奋和方法等内容,欢迎下载使用。













