






苏科版八年级上册6.2 一次函数课文内容课件ppt
展开一根长20cm的弹簧,一端固定,另一端挂物体.在弹簧伸长后的长度不超过30cm的限度内,每挂1kg质量的物体,弹簧伸长0.5cm,如果所挂物体的质量是x kg,弹簧的长度是y cm.问题一:求x与y之间的函数关系式,并画出函数的图像.
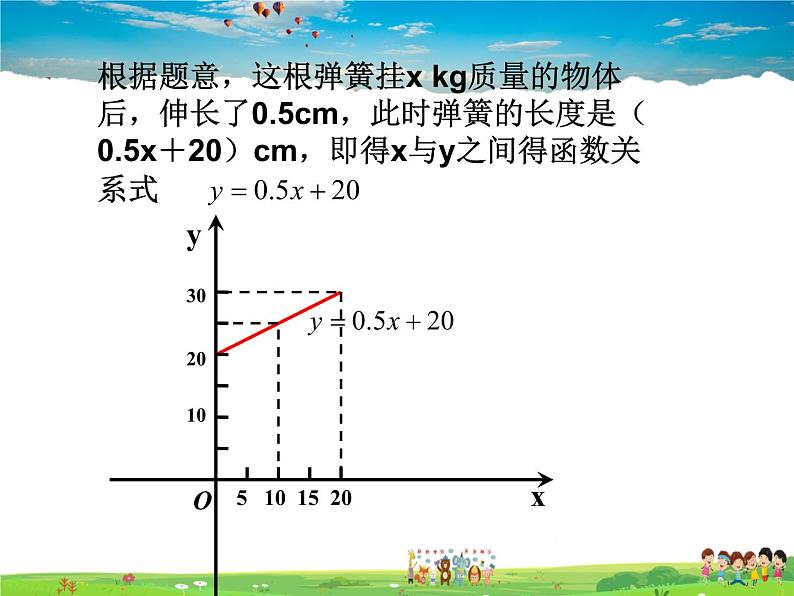
根据题意,这根弹簧挂x kg质量的物体后,伸长了0.5cm,此时弹簧的长度是(0.5x+20)cm,即得x与y之间得函数关系式
所以该弹簧所挂物体的最大质量是20kg.
因为所挂物体越重,弹簧伸得越长,又因为挂上物体后弹簧得长度不能超过30cm,所以当y=30时,该弹簧所挂物体得质量最大。解一元一次方程
问题二:求该弹簧所挂物体得最大质量.
小组交流: 问题一:你能不能用一元一次不等式的方法来求该弹簧所挂物体得最大质量?
问题二:通过上述问题请你谈谈一元一次不等式与一元一次方程、一次函数之间存在怎样的关系?
(1)当一次函数中的一个变量的值确定时,可以用一元一次方程确定另一个变量的值;(2)当已知一次函数中的一个变量取值的范围时,可以用一元一次不等式(组)确定另一个变量取值的范围.
某人点燃一根长25cm的蜡烛,已知蜡烛每小时缩短5cm,设x h后蜡烛剩下的长度为y cm.(1)求y与x之间的函数关系式.(2)几小时后,蜡烛的长度不足10cm?
解:(1)根据题意,得y=25-5x,即y与x之间的函数关系为y=25-5x.(2)当y<10时,25-5x<10,解这个不等式,得x>3.所以3小时后蜡烛的长度不足
求ax+b>0(a≠0)的解
x为何值时y=ax+b的值大于0
确定直线y=ax+b在x轴上方的图象所对应的x值
解(1)移项得:5x - 3x > 10 - 6
合并,得 2x > 4
∴原不等式的解是: x>2
化系数为1,得x >2
(2)作出函数 y = 2x -4 的图象(如图)
从图知观察知,当x>2时 y 的值在x轴上方,即 y > 0
因此当 x > 2 时函数的值大于0。
用画函数图象的方法解不等式5x+4<2x+10
解法1:原不等式化为3x -6<0,
画出直线y = 3x -6(如图)
可以看出,当x<2 时这条直线上的点在x轴的下方,
即这时y = 3x -6 <0所以不等式的解集为x<2
解法2:画出函数 y = 2x+10与 y = 5x+4图象
从图中看出:当x <2时
直线 y = 5x +4 在 y = 2x +10的下方
即 5x+4 < 2x +10
∴ 不等式 5x+4 < 2 x +10 的解集是
已知一次函数 y = 2x+1,根据它的图象回答下列问题. (1) x 取什么值时,函数值 y 为1? (2) x 取什么值时,函数值 y 大于3? (3) x 取什么值时,函数值 y 小于3?
解:作出函数 y = 2x+1的图象
及直线y = 3 (如图)
(1)当 x = 0.5时,函数值 y 为1。
(2)当x > 1.5 时,函数值 y 大于3。
(3)当x <1 .5时,函数值 y 小于3。
利用图象求不等式6x-3<x+2的解集
将方程变形为ax+b<0的形式
画图象(观察x在什么范围时图象上的点是x轴下方)
把不等式6x-3<x+2的两边看成是两个函数:即y1=6x-3,y2=x+2
(观察x在什么范围时图象 y1点在y2点的下方)
所以不等式6x-3<x+2的解是x<1
1.范围为什么时,函数y=2x+6的值满足以下条件? (1) y=0 (2)y>02.利用图像解不等式:5x-1 >2x+5
3.作出函数y=-2x-5的图象,观察图象回答下列问题: ① x取什么值时,-2x-5=0? ② x取什么值时,-2x-5>0? ③ x取什么值时,-2x-5≤0? ④ x取什么值时,-2x-5<0?
4.若y1=-x+3,y2=3x+4,当x取何值时,y1>y2?
5.兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑.已知弟弟每秒跑3m,哥哥每秒跑4m.列出函数关系式,作出函数图象,观察图象回答下列问题:(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?(3)谁先跑过20m?谁先跑过100m?
弟弟先跑过20m,哥哥先跑过100米
通过这节课的学习,你有什么收获?
用一次函数图象来解一元一次不等式
一次函数、一元一次不等式之间的联系
由上面两个问题的关系,能进一步得到“解不等式ax+b >0或ax+b < 0(a,b为常数)”与“求自变量x为何值时,一次函数y = ax+b 的函数值大于0或一次函数y = ax+b 的函数值小于0”有什么关系?
由于任何一元一次不等式都可以转化为ax+b>0或ax+b < 0(a,b为常数a≠0)的形式,所以解一元一次不等式可以转化为:当一次函数值大(小)于0时,求自变量相应的取值范围。
初中数学苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式课文配套ppt课件: 这是一份初中数学苏科版八年级上册<a href="/sx/tb_c100324_t3/?tag_id=26" target="_blank">6.6 一次函数、一元一次方程和一元一次不等式课文配套ppt课件</a>,共22页。PPT课件主要包含了x=2等内容,欢迎下载使用。
苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式课前预习ppt课件: 这是一份苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式课前预习ppt课件,共21页。PPT课件主要包含了提出问题创设情境,我们来看下面的问题,解得x>2,得出x>2时,导入新课,同一个问题,y3x-6,x+4<2x+10,解法一,由图像可以看出等内容,欢迎下载使用。
初中苏科版6.6 一次函数、一元一次方程和一元一次不等式课文配套课件ppt: 这是一份初中苏科版6.6 一次函数、一元一次方程和一元一次不等式课文配套课件ppt,共14页。PPT课件主要包含了热身训练,归纳总结,巩固练习,y=kx+4,变式训练,能力提升等内容,欢迎下载使用。













