初中数学苏科版八年级上册4.3 实数图片ppt课件

这是一份初中数学苏科版八年级上册4.3 实数图片ppt课件，共27页。PPT课件主要包含了1平方根，平方根的定义，平方根的性质，立方根的定义，计算并归纳结论，你知道吗，实数实数的分类，有理数，无理数，平方法比较大小等内容，欢迎下载使用。

1、进一步巩固对无理数，平方根，立方根的认识;2、能运用实数的运算解决简单的实际问题.
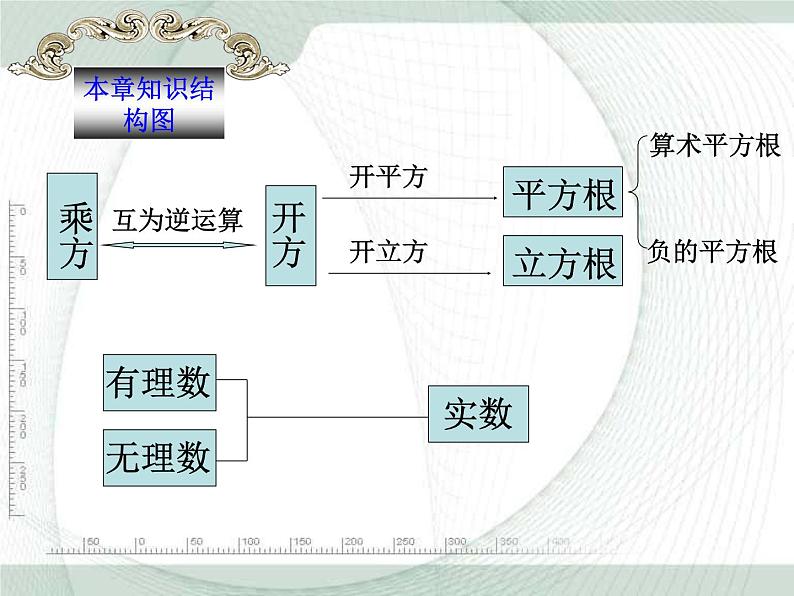
一．数的开方主要知识点1、平方根2、算术平方根3、立方根
1、 的平方是64，所以64的平方根是 ；5的平方根是 。 2、 的平方根是它本身。3、当x 时， 有意义。4、一个正数的两个平方根分别是m和m-4，则m的值是多少？这个正数是多少？
5、一个数的算术平方根等于它本身，这个数是 。6、若x²=16，则5-x的算术平方根是 。 7、若 ＝0，则m=_____，n＝_____。8、一个数的立方根等于它本身，这个数是______
一般地，如果一个数的平方等于a ，那么这个数就叫做a 的平方根（或二次方根）．
　这就是说，如果x 2 = a ，那么 x 就叫做 a 的 ．x=
正数 平方根，它们 ；0的平方根是 ；负数 。
特殊：0的算术平方根是0。
2.算术平方根的定义：
一般地，如果一个数的立方等于a，那么这个数就叫做a的 ，也叫做a的 ．记作　　 .
你知道算术平方根、平方根、立方根联系和区别吗？
求一个数的平方根的运算叫开平方
求一个数的立方根的运算叫开立方
把下列各数分别填入相应的集合内：
有限小数及无限循环小数
判断下列说法是否正确：
1.实数不是有理数就是无理数。 （ ）2.无限小数都是无理数。 （ ）3.无理数都是无限小数。 （ ）4.带根号的数都是无理数。 （ ） 5.两个无理数之和一定是无理数。（ ）6.所有的有理数都可以在数轴上表示，反过来，数轴上所有的点都表示有理数。（ ）
2、比较- 0.5 与 的大小
1、比较 与 2的大小
总结；对于含有根号的数比较大小我们可以采用平方的方法去掉根号之后在进行比较，且两个正数平方大的大，两个负数平方大的反而小
3、怎样比较 与 的大小
例1、已知5x﹣1的平方根为±3，4x+2y+1的立方根是1，求4x﹣2y的平方根．
例2、y= ，求3x+2y的算术平方根.
例3、设 的整数部分和小数部分，分别是x、y，试求x、y的值
1、已知M是满足不等式 的所有整数的和，N是满足不等式x≤ 的最大整数，求M＋N的平方根.2、已知 ，求 的值；
通过这节课的学习,你有何收获?
通过这节课的复习,你有何收获?
1、 的平方根等于_______
2、若x²=16，则12-x的立方根是_____3、若4a+1的平方根是±5，则2a²-8立方根是_____.