数学八年级上册第十一章 三角形综合与测试精品课后复习题

这是一份数学八年级上册第十一章 三角形综合与测试精品课后复习题，共13页。试卷主要包含了将一副三角尺叠放在一起，探究与发现，旧知新意等内容，欢迎下载使用。



1．【问题背景】（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B＝∠C+∠D；


【问题探究】


（2）如图2，直线AP平分△BAO的外角∠FAD，CP平分△OCD的外角∠BCE，若∠ABC＝32°，∠ADC＝22°，求∠P的度数．

















2．如图，∠XOY＝90°，点A，B分别在射线OX，OY上移动，BE是∠ABY的平分线，BE的反向延长线与∠OAB的平分线相交于点C，试问∠ACB的大小是否发生变化，如果不变，求出∠C的度数．























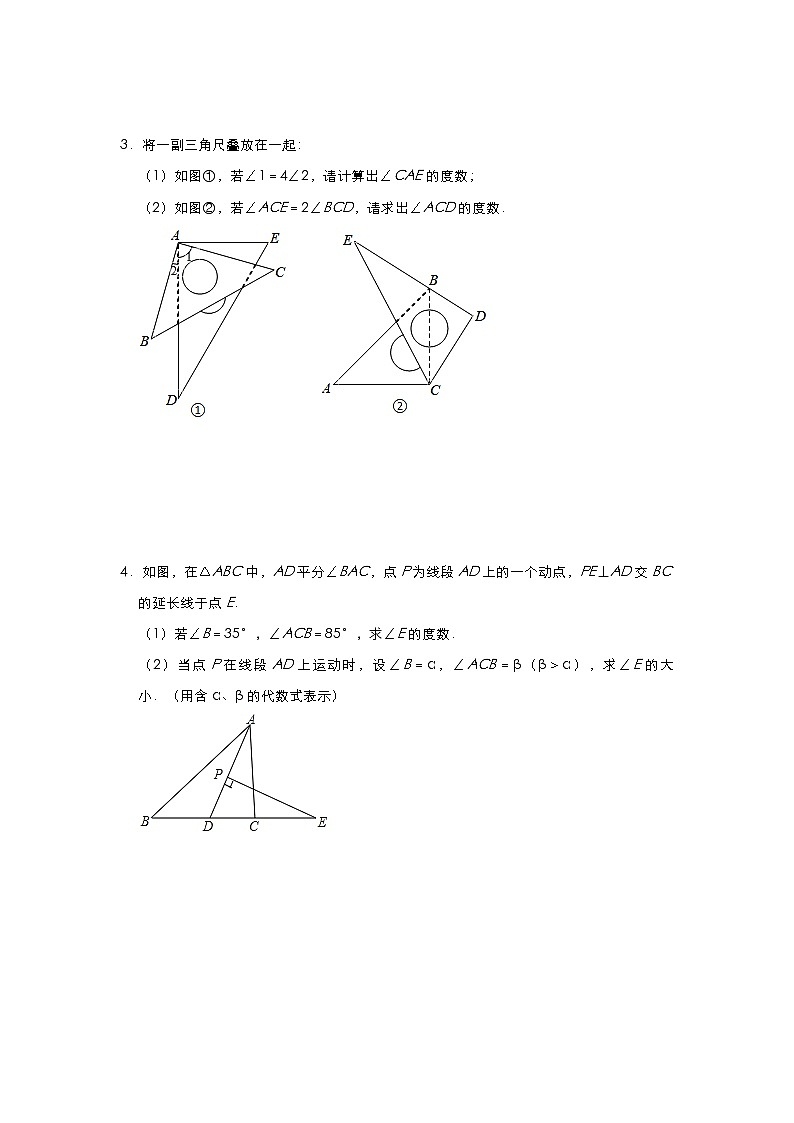
3．将一副三角尺叠放在一起：


（1）如图①，若∠1＝4∠2，请计算出∠CAE的度数；


（2）如图②，若∠ACE＝2∠BCD，请求出∠ACD的度数．

















4．如图，在△ABC中，AD平分∠BAC，点P为线段AD上的一个动点，PE⊥AD交BC的延长线于点E．


（1）若∠B＝35°，∠ACB＝85°，求∠E的度数．


（2）当点P在线段AD上运动时，设∠B＝α，∠ACB＝β（β＞α），求∠E的大小．（用含α、β的代数式表示）


























5．已知，如图，在△ABC中，∠A＝∠ABC，直线EF分别交△ABC的边AB，AC和CB的延长线于点D，E，F．


（1）求证：∠F+∠FEC＝2∠A；


（2）过B点作BM∥AC交FD于点M，试探究∠MBC与∠F+∠FEC的数量关系，并证明你的结论．














6．探究与发现：如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”，


（1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；


（2）请你直接利用以上结论，解决以下三个问题：


①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，∠A＝40°，则∠ABX+∠ACX＝ °；


②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE＝40°，∠DBE＝130°，求∠DCE的度数；


③如图4，∠ABD，∠ACD的10等分线相交于点G1、G2…、G9，若∠BDC＝133°，∠BG1C＝70°，求∠A的度数．








7．旧知新意：


我们容易证明，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？





尝试探究：


（1）如图1，∠DBC与∠ECB分别为△ABC的两个外角，试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系？为什么？


初步应用：


（2）如图2，在△ABC纸片中剪去△CDE，得到四边形ABDE，∠1＝130°，则∠2﹣∠C＝ ；


（3）小明联想到了曾经解决的一个问题：如图3，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有何数量关系？请利用上面的结论直接写出答案 ．


拓展提升：


（4）如图4，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，∠P与∠A、∠D有何数量关系？为什么？（若需要利用上面的结论说明，可接使用，不需说明理由．）








8．在△ABC中，∠ABC的平分线与在∠ACE的平分线相交于点D．


（1）若∠ABC＝70°，∠ACB＝30°，求∠A和∠D的度数；


（2）由（1）小题的计算结果，猜想，∠A和∠D有什么数量关系，并加以证明．








9．如图，四边形ABCD中，∠B＝∠D＝90°，点G，A，B在同一条直线上，点H，C，D在同一条直线上．


（1）图①中，AE，CF分别是∠BAD和∠DCB的平分线，则AE与CF的位置关系？


（2）图②中，AE，CF分别是∠GAD和∠HCB的平分线，则AE与CF的位置关系？


（3）图③中，AE，CF分别是∠BAD和∠HCB的平分线，则AE与CF的位置关系？


（4）请从（1）（2）（3）题中任选一个，证明你得出的结论．




















10．如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC＝60°，∠C＝50°，求∠DAC及∠BOA的度数．




















参考答案


1．（1）证明：在△AOB中，∠A+∠B+∠AOB＝180°，


在△COD中，∠C+∠D+∠COD＝180°，


∵∠AOB＝∠COD，


∴∠A+∠B＝∠C+∠D；


（2）如图2，


∵AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，


∴∠1＝∠2，∠3＝∠4，


∴∠PAD＝180°﹣∠2，∠PCD＝180°﹣∠3，


∵∠P+（180°﹣∠1）＝∠D+（180°﹣∠3），∠P+∠1＝∠B+∠4，


∴2∠P＝∠B+∠D，


∴∠P＝（∠B+∠D）＝×（32°+22°）＝27°．





2．解：∵∠ABY＝90°+∠OAB，AC平分∠OAB，BE平分∠ABY，


∴∠4＝∠ABY＝（90°+∠OAB）＝45°+∠OAB，


即∠4＝45°+∠1，


又∵∠4＝∠C+∠1，


∴∠C＝45°．


3．解：（1）∵∠BAC＝90°，


∴∠1+∠2＝90°，


∵∠1＝4∠2，


∴4∠2+∠2＝90°，


∴∠2＝18°，


又∵∠DAE＝90°，


∴∠1+∠CAE＝∠2+∠1＝90°，


∴∠CAE＝∠2＝18°；





（2）∵∠ACE+∠BCE＝90°，


∠BCD+∠BCE＝60°，


∴∠ACE﹣∠BCD＝30°，


又∠ACE＝2∠BCD，


∴2∠BCD﹣∠BCD＝30°，


∠BCD＝30°，


∴∠ACD＝∠ACB+∠BCD＝90°+30°＝120°．


4．解：（1）∵∠B＝35°，∠ACB＝85°，∠B+∠ACB+∠BAC＝180°．


∴∠BAC＝60°．


∵AD平分∠BAC．


∴∠DAC＝30°．


∵∠ACB＝85°，∠ACB+∠DAC+∠PDE＝180°．


∴∠PDE＝65°．


又∵PE⊥AD．


∴∠DPE＝90°．


∵∠PDE+∠DPE+∠E＝180°．


∴∠E＝25°．


（2））∵∠B＝α，∠ACB＝β，∠B+∠ACB+∠BAC＝180°．


∴∠BAC＝180°﹣α﹣β．


∵AD平分∠BAC．


∴∠DAC＝（180°﹣α﹣β）．


∵∠ACB＝β，∠ACB+∠DAC+∠PDE＝180°．


∴∠PDE＝180°﹣β﹣（180°﹣α﹣β）＝90°．


又∵PE⊥AD．


∴∠DPE＝90°．


∵∠PDE+∠DPE+∠E＝180°．


∴∠E＝180°﹣90°﹣（90°）＝．


5．（1）证明：∵∠FEC＝∠A+∠ADE，∠F+∠BDF＝∠ABC，


∴∠F+∠FEC＝∠F+∠A+∠ADE，


∵∠ADE＝∠BDF，


∴∠F+∠FEC＝∠A+∠ABC，


∵∠A＝∠ABC，


∴∠F+∠FEC＝∠A+∠ABC＝2∠A．


（2）∠MBC＝∠F+∠FEC．


证明：∵BM∥AC，


∴∠MBA＝∠A，、


∵∠A＝∠ABC，


∴∠MBC＝∠MBA+∠ABC＝2∠A，


又∵∠F+∠FEC＝2∠A，


∴∠MBC＝∠F+∠FEC．


6．解：（1）如图（1），连接AD并延长至点F，


，


根据外角的性质，可得


∠BDF＝∠BAD+∠B，∠CDF＝∠C+∠CAD，


又∵∠BDC＝∠BDF+∠CDF，∠BAC＝∠BAD+∠CAD，


∴∠BDC＝∠A+∠B+∠C；





（2）①由（1），可得


∠ABX+∠ACX+∠A＝∠BXC，


∵∠A＝40°，∠BXC＝90°，


∴∠ABX+∠ACX＝90°﹣40°＝50°，


故答案为：50．





②由（1），可得


∠DBE＝∠DAE+∠ADB+∠AEB，


∴∠ADB+∠AEB＝∠DBE﹣∠DAE＝130°﹣40°＝90°，


∴（∠ADB+∠AEB）＝90°÷2＝45°，


∴∠DCE＝（∠ADB+∠AEB）+∠DAE


＝45°+40°


＝85°；





③∠BG1C＝（∠ABD+∠ACD）+∠A，


∵∠BG1C＝70°，


∴设∠A为x°，


∵∠ABD+∠ACD＝133°﹣x°


∴（133﹣x）+x＝70，


∴13.3﹣x+x＝70，


解得x＝63，


即∠A的度数为63°．


7．解：（1）∠DBC+∠ECB


＝180°﹣∠ABC+180°﹣∠ACB


＝360°﹣（∠ABC+∠ACB）


＝360°﹣（180°﹣∠A）


＝180°+∠A；





（2）∵∠1+∠2＝∠180°+∠C，


∴130°+∠2＝180°+∠C，


∴∠2﹣∠C＝50°；





（3）∠DBC+∠ECB＝180°+∠A，


∵BP、CP分别平分外角∠DBC、∠ECB，


∴∠PBC+∠PCB＝（∠DBC+∠ECB）＝（180°+∠A），


在△PBC中，∠P＝180°﹣（180°+∠A）＝90°﹣∠A；


即∠P＝90°﹣∠A；


故答案为：50°，∠P＝90°﹣∠A；





（4）延长BA、CD于Q，


则∠P＝90°﹣∠Q，


∴∠Q＝180°﹣2∠P，


∴∠BAD+∠CDA＝180°+∠Q，


＝180°+180°﹣2∠P，


＝360°﹣2∠P．





8．解：（1）在△ABC中，∠ABC＝70°，∠ACB＝30°，


∴∠A＝180°﹣∠ABC﹣∠ACB＝80°，


∵BD为∠ABC，CD为∠ACE的角平分线，


∴∠DBC＝∠ABC＝×70°＝35°，


∠ACD＝（180°﹣∠ACB）＝×150°＝75°，


∴∠D＝180°﹣∠DBC﹣∠ACB﹣∠ACD＝180°﹣35°﹣30°﹣75°＝40°，


∴∠A＝80°，∠D＝40°；





（2）通过第（1）的计算，得到∠A＝2∠D，理由如下：


∵∠ACE＝∠A+∠ABC，


∴∠ACD+∠ECD＝∠A+∠ABD+∠DBE，∠DCE＝∠D+∠DBC，


又∵BD平分∠ABC，CD平分∠ACE，


∴∠ABD＝∠DBE，∠ACD＝∠ECD，


∴∠A＝2（∠DCE﹣∠DBC），∠D＝∠DCE﹣∠DBC，


∴∠A＝2∠D．


9．解：（1）图1中AE∥FC；


（2）图2中AE∥FC；


（3）图3中AE⊥FC．





（4）选择图1证明．如图1：


∵∠BAD+∠BCD＝∠1+∠2+∠3+∠4＝360°﹣（∠B+∠D）＝360°﹣180°＝180°，


又∵AE、CF分别是∠BAD和∠DCB的内角平分线，


∴∠1+∠3＝∠BAD+∠BCD＝（∠BAD+∠BCD）＝×180°＝90°．


又∵∠B＝90°，


∴∠1+∠5＝90°，


∴∠3＝∠5，


∴AE∥FC；


选择图2证明，如图2，


∵∠B＝∠D＝90°，


∴∠BAD+∠BCD＝360°﹣2×90°＝180°，


∴∠BAD+∠BCD＝90°，


∴∠GAD＝∠BCD，


∵AE是∠GAD的角平分线，


∴∠1＝∠GAD＝∠BCD，


同理可得：∠2＝∠BAD，


∴∠1+∠BAD＝90°，


延长CD交AE于点P，∠ADC＝90°，


∴∠1+∠P＝90°，


∴∠P＝∠BAD，


即∠P＝∠2，


∴AE∥FC（同位角相等，两直线平行）；


选择图3证明．如图3：


∵∠B+∠BAD+∠D+∠DCB＝360°，


又∵∠B＝∠D＝90°，


∴∠BAD+∠DCB＝180°，


∵∠DCB+∠BCE＝180°，


∴∠BAD＝∠BCE，


∵AE、AF分别是∠BAD和∠DCB的内角平分线和外角平分线，


∴∠1＝∠BAD，∠2＝∠BCE，


∴∠1＝∠2，


∵∠3＝∠4，∠1+∠B+∠4＝180°，∠2+∠CMA+∠3＝180°，


∵∠B＝90°∠1+∠4＝∠2+∠3，


∴∠CMA＝∠B＝90．


∴AE⊥CF．








10．解：∵在△ABC中，AD是高，


∴∠ADC＝90°，


∵在△ACD中，∠C＝50°，


∴∠DAC＝90°﹣50°＝40°，


∵在△ABC中，∠C＝50°，∠BAC＝60°，


∴∠ABC＝70°，


∵在△ABC中，AE，BF是角平分线，


∴∠EAC＝∠BAC＝30°，∠FBC＝∠ABC＝35°，


∴∠BOA＝∠BEA+∠FBC＝∠C+∠EAC+∠FBC＝50°+30°+35°＝115°．