



数学九年级上册第23章 图形的相似23.2 相似图形评优课ppt课件
展开1.掌握相似三角形的判定定理1;(重点)2.经历相似三角形的判定定理1的探究过程.(难点)
1.观察学生与老师的直角三角板(30°与60°),会相似吗?测量测量,得出你的猜想.
2. 两个人画出两个三角形 ,使三个角分别为60°,45°, 75° .
①分别量出两个三角形三边的长度;②这两个三角形相似吗?
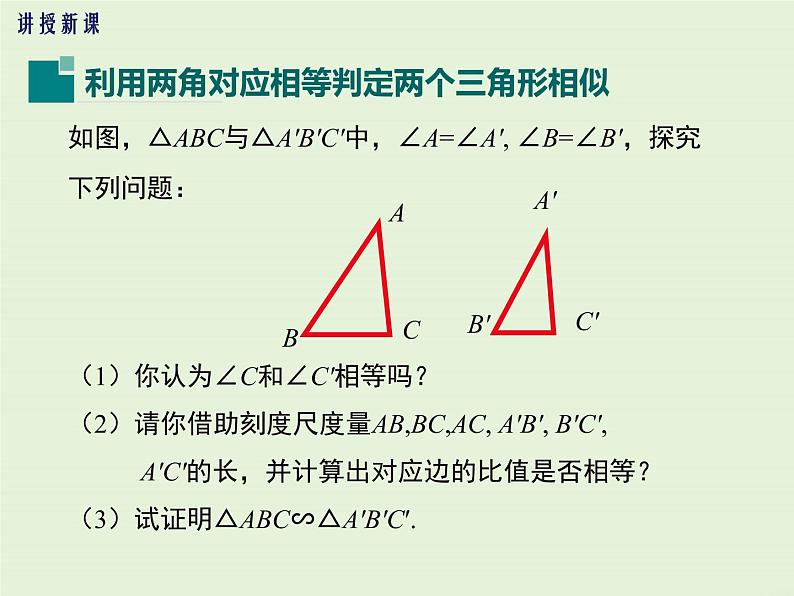
如图,△ABC与△A′B′C′中,∠A=∠A′, ∠B=∠B′,探究下列问题:(1)你认为∠C和∠C′相等吗?(2)请你借助刻度尺度量AB,BC,AC, A′B′, B′C′, A′C′的长,并计算出对应边的比值是否相等?(3)试证明△ABC∽△A′B′C′.
(1)解:在△ABC中,∠C=180°-∠A - ∠B 在△A′B′C′中,∠C′=180° - ∠A′ - ∠B′ ∵ ∠A=∠A′, ∠B=∠B′ ∴ ∠C= ∠C′
(2)解:借助刻度尺度量发现,
(3)证明:在△ABC的边 AB(或AB的延长线)上,截取AD=A′B′,过点 D 作DE//BC,交AC于点 E,则有△ADE∽△ABC ∵∠ADE=∠B, ∠B=∠B′, ∴∠ADE=∠B′. 又∵∠A=∠A′, AD=A′B′, ∴△ADE≌△A′B′C′, ∴△A′B′C′∽△ABC.
∵ ∠A=∠A', ∠B=∠B'
∴ △ABC ∽ △A'B'C'
(两个角分别相等的两个三角形相似)
1.判断题:⑴所有的直角三角形都相似.( ) ⑵所有的等边三角形都相似.( )⑶所有的等腰直角三角形都相似.( ) ⑷有一个角相等的两等腰三角形相似.( )
2.已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
证明: ∵∠BAC= ∠1+ ∠DAC , ∠DAE= ∠3+ ∠DAC, ∵ ∠1=∠3,∴ ∠BAC=∠DAE. ∵ ∠C=180°-∠2-∠DOC ,∠E=180°-∠3-∠AOE. 又∵ ∠DOC =∠AOE(对顶角相等), ∴ ∠C= ∠E. 在△ABC和△ ADE中 ∠BAC=∠DAE,∠C= ∠E ∴ △ABC∽△ADE
初中数学华师大版九年级上册2. 相似三角形的判定教学ppt课件: 这是一份初中数学华师大版九年级上册2. 相似三角形的判定教学ppt课件,共17页。PPT课件主要包含了知识要点,新知导入,课程讲授,∵∠B∠B′,∴∠ADE∠B′,解∵ED⊥AB,随堂练习,证明∵AB∥DE,∴∠B∠DEF,∠ACB∠F等内容,欢迎下载使用。
初中数学华师大版九年级上册2. 相似三角形的判定教学课件ppt: 这是一份初中数学华师大版九年级上册2. 相似三角形的判定教学课件ppt,共17页。PPT课件主要包含了知识要点,新知导入,课程讲授,∵∠B∠B′,∴∠ADE∠B′,解∵ED⊥AB,随堂练习,证明∵AB∥DE,∴∠B∠DEF,∠ACB∠F等内容,欢迎下载使用。
冀教版九年级上册25.4 相似三角形的判定教学ppt课件: 这是一份冀教版九年级上册25.4 相似三角形的判定教学ppt课件,共21页。













