人教版八年级上册第十二章 全等三角形综合与测试教案

这是一份人教版八年级上册第十二章 全等三角形综合与测试教案，共9页。

复习纲要：


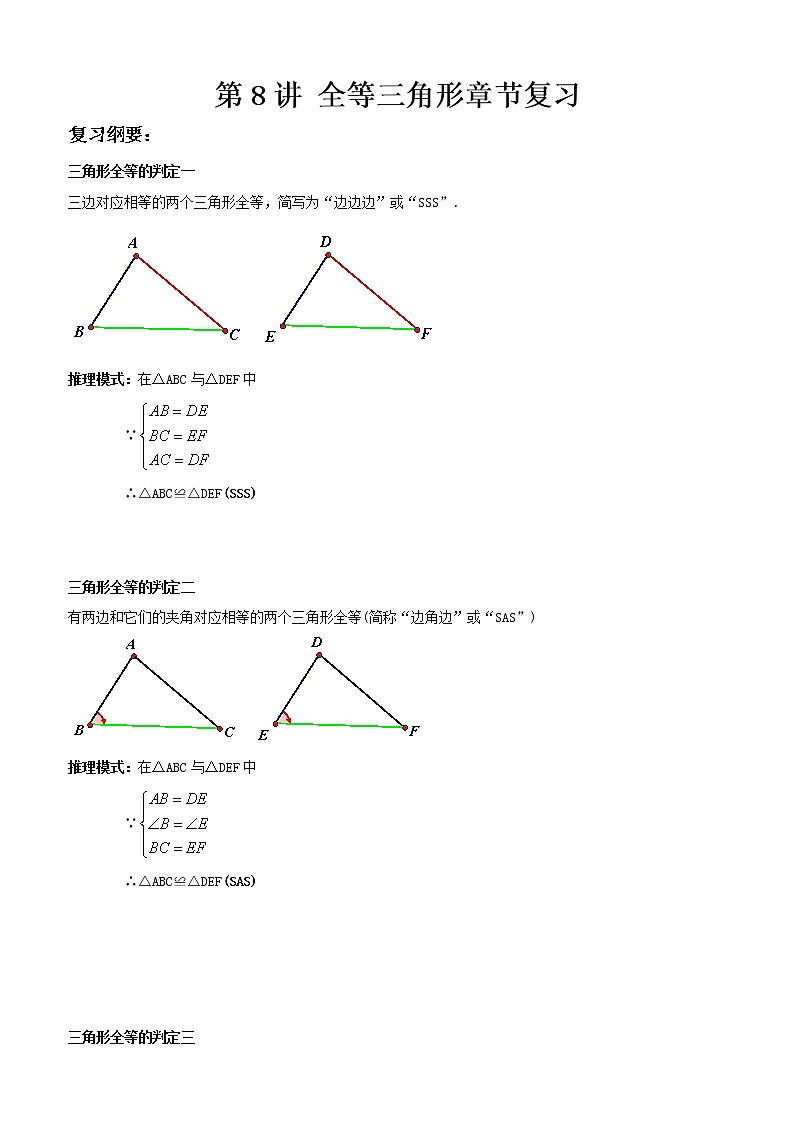
三角形全等的判定一


三边对应相等的两个三角形全等，简写为“边边边”或“SSS”．





推理模式：在△ABC与△DEF中


∵


∴△ABC≌△DEF(SSS)


淘宝店：期望数学岛





三角形全等的判定二


有两边和它们的夹角对应相等的两个三角形全等(简称“边角边”或“SAS”)





推理模式：在△ABC与△DEF中


∵


∴△ABC≌△DEF(SAS)














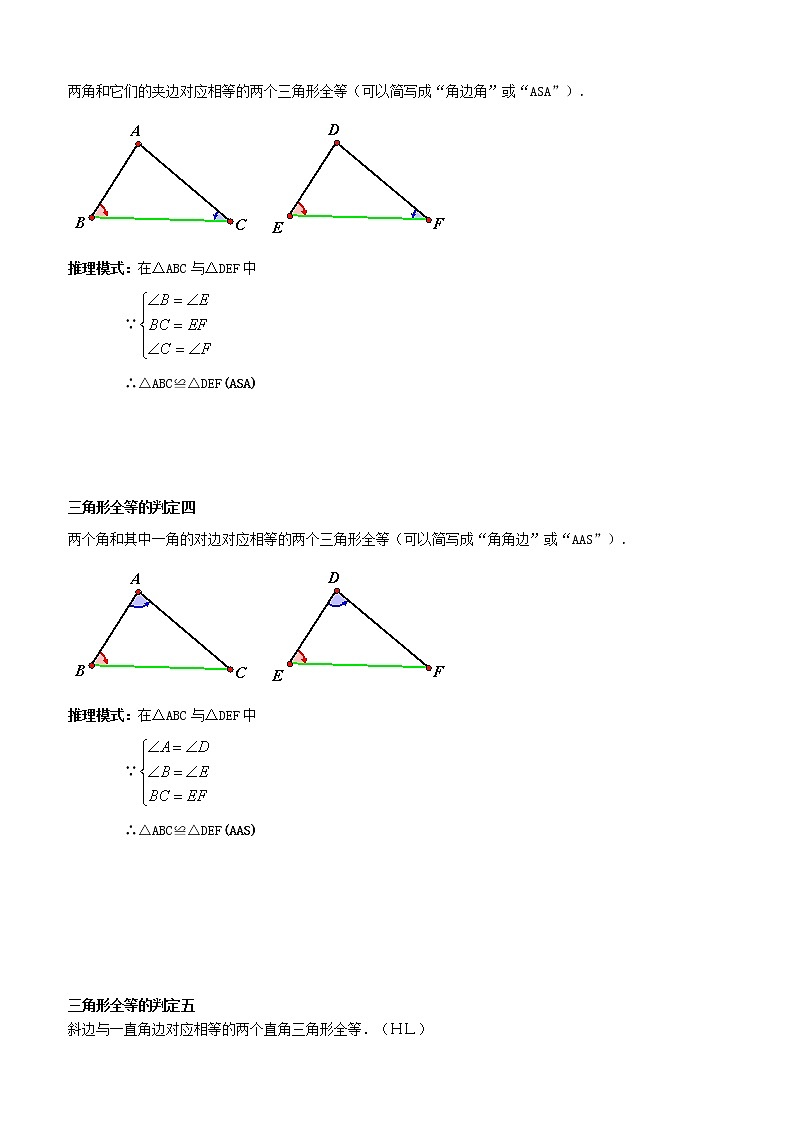
三角形全等的判定三


两角和它们的夹边对应相等的两个三角形全等（可以简写成“角边角”或“ASA”）．





推理模式：在△ABC与△DEF中


∵


∴△ABC≌△DEF(ASA)











三角形全等的判定四


两个角和其中一角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS”）．





推理模式：在△ABC与△DEF中


∵


∴△ABC≌△DEF(AAS)























三角形全等的判定五


斜边与一直角边对应相等的两个直角三角形全等．（ＨＬ）





推理模式：在Rt△ABC与Rt△DEF中


∵


∴△ABC≌△DEF(HL)








特别注意：全等三角形的判定中没有边边角定理，即不存在SSA定理


反例如图：在△ABC与△DEF中，AB=DE,AC=DF,,显然这两个三角形不全等。








角平分线的性质定理：角平分线上的点到角两边的距离相等。





推理模式：∵


于,于


∴





角平分线的判定定理：到一个角的两边的距离相等的点，在这个角的平分线上。





推理模式：∵于,于,


∴点在的平分线上（或）期望数学岛淘宝店





典例分析


例1.已知：如图，∠ABC=∠DEF，AB=DE，要说明ΔABC≌ΔDEF


(1) 若以“SAS”为依据，还要添加的条件为


(2) 若以“ASA”为依据，还要添加的条件为


(3) 若以“AAS”为依据，还要添加的条件为























例2.（贵州铜仁9分）如图，E、F是四边形ABCD的对角线BD上的两点，AE∥CF，AE=CF，BE=DF．


求证：△ADE≌△CBF．
































例3.如图，C为线段AB上一点，△ACM和△CBN都是等边三角形，连接AN交MC于E,连接BM交NC于F. 求证：①AN=MB，②CE=CF





























例4.如图，A、E、F、B四点共线，AC⊥CE、BD⊥DF、AE=BF、AC=BD，求证：△ACF≌△BDE.














经典练习：


1、下列条件中，不能判定△ABC≌△A′B′C′的是( )


A、AB=A′B′，∠A=∠A′，AC=A′C′


B、AB=A′B′，∠A=∠A′，∠B=∠B′


C、AB=A′B′，∠A=∠A′，∠C=∠C′


D、∠A=∠A′，∠B=∠B′，∠C=∠C′





2． 在△ABC与△A′B′C′中，已知∠A＝44°15′，∠B＝67°12′，∠C′＝68°33′，∠A′＝44°15′，


且AC＝A′C′，则这两个三角形（ ）


A．一定不全等 B．一定全等 C．不一定全等 D．以上都不对





3．已知ΔABC中，AB=10，BC=15，CA=20，点O是ΔABC内角平分线的交点，(三角形三个内角的平分线交于一点)则ΔABO、 ΔBCO、 ΔCAO的面积比是( )


A．1:1:1 B．1:2:3 C．2:3:4 D．3:4:5








4．如图，已知点E在△ABC的外部，点D在BC边上，DE交AC于F，若∠1=∠2=∠3，AC=AE，则有( )


A．△ABD≌△AFD B．△AFE≌△ADC C．△AEF≌△DFC D．△ABC≌△ADE

















第5题图


第4题图


第3题图








5．如图，AB > AC，点P为ΔABC的角平分线AD上一点，则下列说法正确的是（ ）


A． AB – AC > PB – PC B． AB – AC < PB – PC


C． AB – AC = PB – PC D． 无法确定





6．下列说法不正确的是（ ）


A．有两个角和一条边对应相等的两个三角形全等


B．有一条边和一个锐角对应相等的两个直角三角形全等


C．有两边和其中一边的对角对应相等的两个三角形全等


D．有两条直角边对应相等的两个直角三角形全等





7. 在△ABC中，AC=5，中线AD=4，则边AB的取值范围是( )


A．1




8、如图，在△ABC中，AD平分∠BAC，过B作BE⊥AD于E，过E作


EF∥AC交AB于F，则( )


A、AF=2BF B、AF=BF C、AF>BF D、AF




A


C


D


B





9.如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于D，


若BC=64，且BD：CD=9：7，则点D到AB边的距离为( )


A、18 B、32 C、28 D、24














10．（山东淄博）已知一等腰三角形的腰长为5，底边长为4，底角为β．满足下列条件的三角形不一定与已知三角形全等的是( )


(A)两条边长分别为4，5，它们的夹角为β (B)两个角是β，它们的夹边为4


(C)三条边长分别是4，5，5 (D)两条边长是5，一个角是β








图12


11、如图10所示，有两个长度相同的滑梯(即BC=EF)，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则△ABC≌△DEF，理由是______．











12、如果两个三角形中两条边和其中一边上的高对应相等，那么这两个三角形的第三条边所对的角的关系


是








13. （山东临沂）在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在


AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，


则AE= cm．





14．两块完全相同的三角形纸板ABC和DEF，按如图所示的方式叠放，阴影部分为重叠部分，点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等？为什么？























15．如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，点E为直角三角板的直角顶点，连结BE、EC。试猜想线段BE和EC的数量及位置关系，并证明你的猜想．


A


B


C


D


E


























16.我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等?


(1)阅读与证明：对于这两个三角形均为直角三角形，显然它们全等．对于这两个三角形均为钝角三角形，可证它们全等(证明略)．对于这两个三角形均为锐角三角形，它们也全等，可证明如下：


已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1Cl，∠C=∠Cl．求证：△ABC≌△A1B1C1．


(请你将下列证明过程补充完整)


证明：分别过点B，B1作BD⊥CA于D，


B1 D1⊥C1 A1于D1.


则∠BDC=∠B1D1C1=900，


∵BC=B1C1，∠C=∠C1，


∴△BCD≌△B1C1D1，


∴BD=B1D1．








(2)归纳与叙述：由(1)可得到一个正确结论，请你写出这个结论．














17.如图，PA、PC分别是外角与的平分线，并交于点P，PDBM于点D，PFBN于点F，求证：BP是的平分线。



































思考题


1.已知：如图，在△ABC中，D为BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于点G，DE⊥GF，并交AB于点E，连结EG．


（1）求证BG=CF；


（2）试猜想BE+CF与EF的大小关系，并加以证明．
































2.如图，图（1）中等腰△ABC与等腰△DEC共点于C，且∠BCA＝∠ECD，连结BE，AD，若BC＝AC、EC＝DC．求证：BE＝AD；若将等腰△EDC绕点C旋转至图（2）（3）（4）情况时，其余条件不变，BE与AD还相等吗？为什么?


（1）


（2）


（3）


（4）