初中数学人教版八年级上册14.1.2 幂的乘方教学设计

这是一份初中数学人教版八年级上册14.1.2 幂的乘方教学设计，共3页。教案主要包含了教学目标，重点难点，板书设计，教学反思等内容，欢迎下载使用。




┃教学过程设计┃











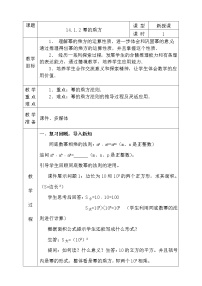
【教学目标】


1.经历探索幂的乘方运算性质的过程，进一步体会幂的意义，能熟练运用幂的乘方公式进行计算.


2.发展学生推理能力和有条理的表达能力，理解幂的乘方运算性质，并纳入已有的知识体系.


【重点难点】


重点：幂的乘方运算.


难点：幂的乘方法则的总结及运用.
教学过程
设计意图
一、复习旧知，导入新课


问题1：(1)33×35； (2)105×106； (3)x2·x4；


(4)y2·y； (5)am·a2； (6)2n－1×2n＋1.
学生口答：(1)38； (2)1011； (3)x6； (4)y3； (5)am＋2； (6)22n.


问题2：同底数幂的乘法法则是什么？分别用语言和字母表示.


同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加.


即am·an＝am＋n(m，n都是正整数).


学生口答，并追问公式am·an＝am＋n(m，n都是正整数)推导过程.


问题3：(62)4，(a2)3表示什么意义？


学生独立回答，如果学生出现困难，小组交流，共同解决.


答案：(62)4表示4个62相乘，(a2)3表示3个a2相乘.
问题1旨在通过具体问题复习同底数幂的乘法法则，避免单纯的记忆公式，通过问题1的复习引入，学生回忆问题2同底数幂的乘法法则，并为幂的乘方公式推导打下基础.
二、师生互动，探究新知


问题1：计算：(1)(62)4；(2)(a2)3.


学生尝试，小组内交流，班内交流.


(1)(62)4＝62×62×62×62


＝62＋2＋2＋2(根据an·am＝an＋m)


＝68；


(2)(a2)3＝a2×a2×a2


＝a2＋2＋2(根据an·am＝an＋m)


＝a6.


问题2：计算：(1)(am)3；(2)(am)n.


学生类比问题1计算，并小组内交流，说出过程.


(am)n(n个am相乘)＝am×am×…×am×aeq^\(m,\s\d4(n个)) \* MERGEFORMAT ＝amn.


问题3：类比同底数幂的乘法的乘法法则，请你尝试用语言叙述以上规律.


学生尝试，教师引导得出结论：


(am)n＝amn(m，n都是正整数)，幂的乘方，底数不变，指数相乘.
三、运用新知，解决问题


1.计算：


(1)(103)5；(2)(a4)4；(3)(am)2；(4)(－x4)3.


2.判断题，错误的予以改正.


(1)a5＋a5＝2a10.( )


(2)(x3)3＝x6.( )


(3)(－3)2·(－3)4＝(－3)6＝－36.( )


(4)x3＋y3＝(x＋y)3.( )


学生独立完成后，口答.
目的是通过第1题让学生体会底数不同情况下要注意对结果进行化简，估计此题错误较多，教师要注意及时点拨，也可适当加变式，进行巩固.第2题主要针对学生以前学过的知识进行综合，防止知识的负迁移，教师教学注意不要急于求成，要给学生充足的时间进行思考、交流、辨析.
四、课堂小结，提炼观点


通过本节课的学习，你有何收获和体会？还有哪些困惑？
五、布置作业，巩固提升


教材第97页练习
【板书设计】


幂的乘方


(am)n＝amn(m，n都是正整数)幂的乘方，底数不变，指数相乘.

【教学反思】


本节课开始以复习同底数幂相乘计算开始，进而回忆同底数幂的乘法法则，让学生自然地进入到新知识的构建，深刻体会到同底数幂相乘与幂的乘方运算之间的联系区别和传承关系，增加了对幂的乘方的学习兴趣.然后又通过类比、从特殊到一般的数学思想方法，了解幂的乘方运算法则的生成过程，通过让学生大胆发言阐述自己的理由，通过学生亲自动手动脑更深刻体会到如何进行幂的乘方运算.