初中数学北师大版（2024）八年级上册7 二次根式课前预习课件ppt

这是一份初中数学北师大版（2024）八年级上册7 二次根式课前预习课件ppt，共60页。PPT课件主要包含了知识回顾，二次根号，被开方数，读作根号a，新知探究，跟踪训练，被开方数为非负数，分母不能为0，2原式5，-aa0等内容，欢迎下载使用。
（1）什么叫一个数的平方根？如何表示？
（2）什么是一个数的算术平方根？如何表示？
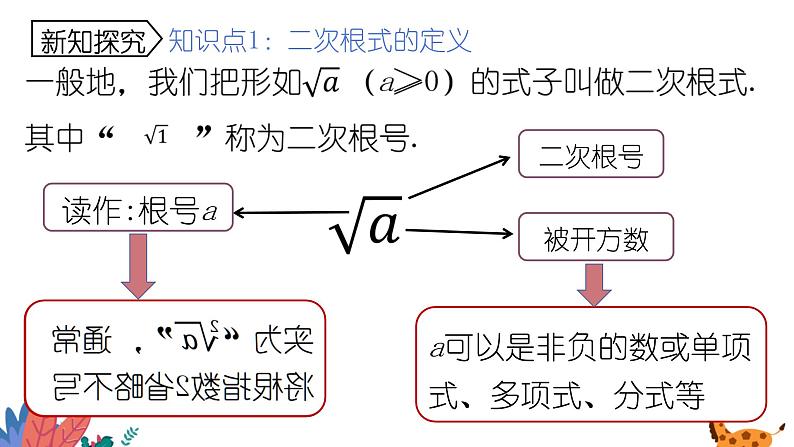
知识点1：二次根式的定义
a可以是非负的数或单项式、多项式、分式等
题中被开方数m-5,mn,-5是负数，不是二次根式
解：由 x2≥0 可知，x 可以为任意实数.由 x3≥0 可知，x≥0.
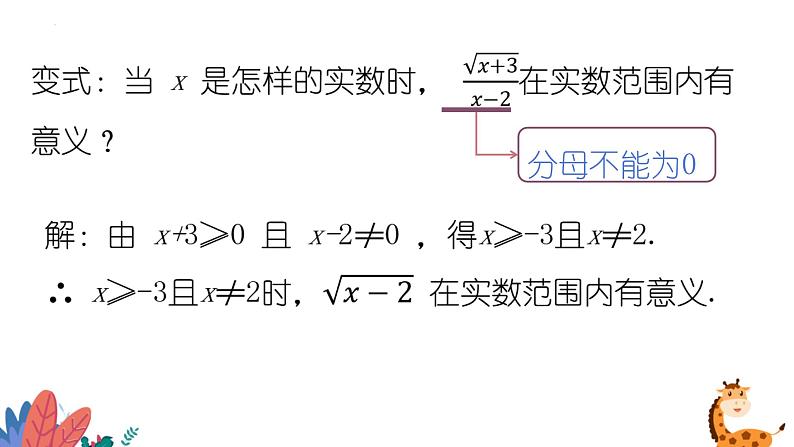
知识点2：二次根式有意义的条件
当 a 是怎样的实数时，下列各式在实数范围内有意义？
当二次根式的被开方数出现完全平方公式或能配方成完全平方公式时，其中所含字母取任意实数，二次根式在实数范围内都有意义.
知识点3：二次根式的性质
文字表述：一个非负数的算术平方根的平方等于这个数本身.
性质3 -a（a0.实际上，公式中a，b的取值范围是限制公式右边的，对于公式左边，只要ab≥0即可.
1.二次根式除法法则的逆用也称为商的算术平方根的性质.
2.公式中的a, b既可以是一个数，也可以是其他代数式.
3.利用商的算术平方根的性质可以对被开方数中含有分母的二次根式进行化简，化成被开方数不含分母的二次根式.
例2 化简：（1）
（2）
化简：（1） ; （2）

最简二次根式：满足以下两个条件的二次根式，叫做最简二次根式.
（1）被开方数不含分母；
（2）被开方数中不含能开得尽方的因数或因式 .
知识点8：最简二次根式
即被开方数必须是整数（式）
注意：在二次根式的运算中，一般要把最后结果化为最简二次根式，并且分母中不含二次根式.
解：∵ S=ab，
例6 设长方形的面积为 S，相邻两边长分别为 a，b. 已知S= ，b= ，求 a.
化简二次根式的一般方法
1.将被开方数中能开得尽方的因数或因式进行开方.
2.化去根号下的分母
①若被开方数中含有带分数，应先将带分数化为假分数.
②若被开方数中含有小数，应先将小数化为分数.
3.被开方数是多项式的要先进行因式分解.
二次根式化成最简二次根式的步骤
分：利用分解因数或分解因式的方法把被开方数的分子、分母都化成质因数（或最简因式）的幂的乘积的形式.
移：把能开得尽方的因数（或因式）用它的算术平方根代替，移到根号外，当把根号内的分母中的因式移到根号外时，要注意依旧写在分母的位置上.
化：化去被开方数中的分母.
约：约分，化为最简二次根式.
1.判断: 下列各式中，哪些是最简二次根式？
2.化简： 将下列各式化简为最简二次根式.
解：（1）∵ ， ∴ a≥0.
1.下列二次根式中，最简二次根式是（ ）.
A. B. C. D.
2.把下列二次根式化成最简二次根式.
（2）
（3）
（4）
3.设长方形的面积为 S，相邻两边的长分别为 a，b. 已知S=16，b= ，求 a.
解：∵S=ab，
同类二次根式：将二次根式化成最简二次根式，若被开方数相同的几个二次根式叫做同类二次根式.
合并的方法：合并二次根式的方法与合并同类项类似，将根号外的因数或因式相加，根指数和被开方数不变，合并的依据是分配律的逆向运用.
知识点9：同类二次根式
二次根式的加减：一般地，二次根式加减时，可以先将二次根式化成最简二次根式，再将被开方数相同的二次根式进行合并.
知识点10：二次根式的加减
注意：（1）化成最简二次根式后，被开方数不同的二次根式不能合并；（2）对于不能合并的二次根式，一定不要漏写，要保持不变，它们也是结果的一部分.
二次根式加减运算的一般步骤1.化：将每个二次根式都化成最简二次根式；2.找：找出被开方数相同的二次根式；3.合：将被开方数相同的二次根式合并成一项.
二次根式的乘除法与二次根式的加减法的
结果化为最简二次根式.
先化为最简二次根式，再合并同类二次根式.
注意：一定要将不能开方的数字和字母作为结果的一部分保留.
1.下列计算正确的是（ ）.
1.二次根式的混合运算种类：二次根式的加、减、乘、除、乘方（或开方）的混合运算.
2.二次根式的混合运算顺序：先乘方，再乘除，最后加减，有括号的先算括号里面的（或先去掉括号），与整式的混合运算顺序相同.
知识点11：二次根式的混合运算
注意：一定要注意二次根式的运算顺序.
3.二次根式的混合运算依据:有理数的运算律（交换律、结合律、分配律）、多项式乘法法则和乘法公式（平方差公式、完全平方公式）在二次根式的运算中仍然适用.
运用类比的思想，将二次根式的混合运算类比成整式的混合运算.
4.二次根式混合运算的几种常见类型及计算方法
一般来说，没有特别说明就将字母默认为大于等于零的数字或式子.
二次根式的混合运算的重点1.二次根式的混合运算结果一定要化成最简形式；2.在进行二次根式的计算时，能用乘法公式的要尽量使用乘法公式，同时要注意公式的正用和逆用，以及简化运算过程.

解：（1）原式=