北师大版（2024）八年级上册1 认识无理数教学演示课件ppt

这是一份北师大版（2024）八年级上册1 认识无理数教学演示课件ppt，共18页。PPT课件主要包含了感悟新知，知识点，无理数的产生，满足a25，无理数的概念，随堂练习等内容，欢迎下载使用。
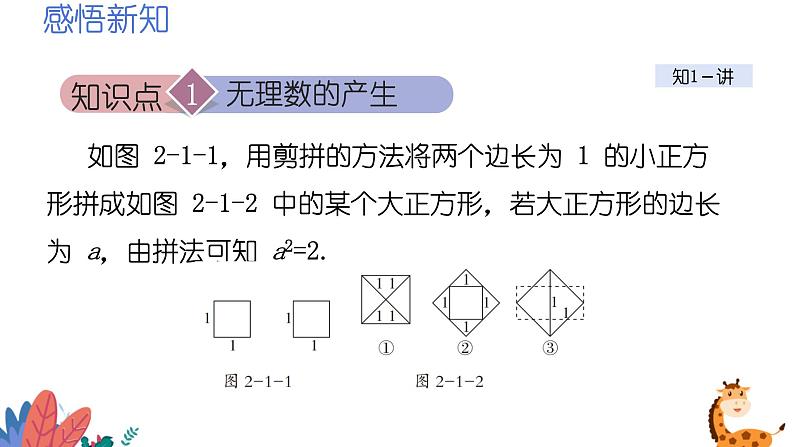
如图 2-1-1，用剪拼的方法将两个边长为 1 的小正方形拼成如图 2-1-2 中的某个大正方形，若大正方形的边长为 a，由拼法可知 a2=2.
特别提醒若x2=a，当a不能写成一个整数或一个分数的平方的形式时，x不是有理数 .
图 2-1-3 是由五个边长为 1 的小正方形组成的图案，如果把它们剪拼成一个正方形 .
解题秘方：根据剪拼没有改变图形的面积，确定正方形的面积及边长，结合勾股定理解释无理数的产生 .
解： 所拼成的正方形的面积是 5.
(1)所拼成的正方形的面积是多少？
(2)设拼成的正方形的边长为 a， a 应满足什么条件？
解：a 不是整数，不是分数，不是有理数 .
(3) a 是整数吗？是分数吗？是有理数吗？
所拼成的正方形如图 2-1-3.
(4)画出你所拼的正方形 .
1.无理数的概念  无限不循环小数称为无理数，如圆周率 π =3.141 592 65…，1.010 010 001…(相邻两个 1 之间 0 的个数逐次加 1)等 .
特别提醒有理数和无理数的区别：1.无理数是无限不循环小数，有理数是有限小数或无限循环小数；2.有理数可化为分数，无理数不能化为分数.
2. 常见无理数的几种类型
解题秘方：紧扣无理数的概念进行逐一识别 .
2.下列说法不正确的是 (　 　)A.所有的整数和分数都是有理数B.无理数一定是无限小数C.无限小数一定是无理数D.无理数不能写成分数的形式
【答案】C　【解析】　根据有理数的定义,整数属于有理数,分数属于有理数,故A正确;无理数都是无限不循环小数,无限循环小数是有理数,故B正确,C错误;分数不是无理数,故D正确.故选C.