









初中数学北师大版八年级上册1 认识无理数一等奖教学ppt课件
展开掌握无理数的概念;能用所学定义正确判断所给数的属性.
借助计算器探索无理数是无限不循环小数,从中体会无限逼近的思想.
2.1 认识无理数第2课时
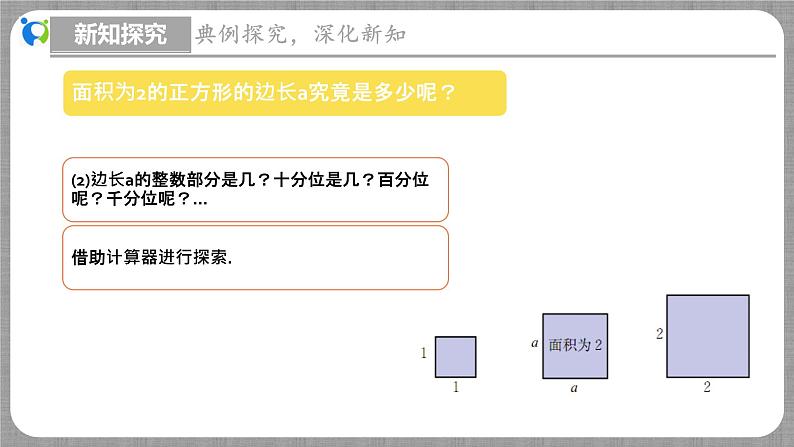
∵12=1,a2=2,22=4,∴1<a2<4,且a>0,∴1<a<2
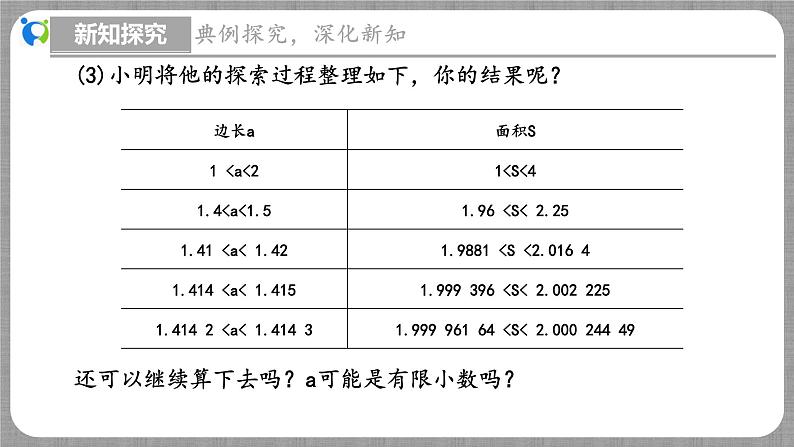
(3)小明将他的探索过程整理如下,你的结果呢?
还可以继续算下去吗?a可能是有限小数吗?
【归纳总结】 a是介于1和2之间的一个数,既不是整数,也不是分数,则a一定不是有理数.如果写成小数形式,a=1.41421356…,它是一个无限不循环小数.
【做一做】(1)估计面积为5的正方形的边长b的值(结果精确到十分位 ),并用计算器验证你的估计.(2)如果结果精确到百分位呢?
精确到0.1,b≈2.2,精确到0.01,b≈2.24
事实上,b=2.236 067 978…它是一个无限不循环小数.
同样,对于体积为2的正方体,借助计算器,可以得到它的棱长c=1.259 921 05…它也是一个无限不循环小数.
【议一议】 把下列各数表示成小数,你发现了什么?
事实上,有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限循环小数也都是有理数.
(1)无理数的定义:无限不循环小数称为无理数. (2)无理数的类型: ①上述中的a,b,c类型的; ②圆周率π是一个无限不循环小数,它也是一个无理数; ③如0.585 885 888 588 885…(相邻两个5之间8的个数逐次加1),也是无理数。
【例】下列各数中,哪些是有理数?哪些是无理数?
1.下列说法中正确的是( ) A.无限小数都是无理数 B.有限小数是无理数 C.无理数都是无限小数 D.有理数是有限小数
3.一个直角三角形两条直角边的长分别是3和5,则斜边长a是有理数吗?
解:由勾股定理得: a2=32+52,即a2=34.因为不存在有理数的平方等于34,所以a不是有理数.
4. 面积为3的正方形的边长为x,则x ( ) A.1
解: (1)∵πa2=20π,∴a2=20. a不是有理数,因为a既不是整数,也不是分数,而是无限不循环小数. (2)a≈4.5. (3)a≈4.47.
1.无理数的特征: (1)无理数的小数部分位数无限. (2)无理数的小数部分不循环,不能表示成分数的形式.2.常见的无理数的形式: (1)无限不循环的小数; (2)特殊字母,如“π”; (3)an=b(n为大于1的自然数)中b为有理数,则a可能为无理数.
求证:若r,s是有理数且r≠0,α是无理数,则rα+s是无理数.
初中北师大版2 定义与命题获奖教学课件ppt: 这是一份初中北师大版<a href="/sx/tb_c91901_t3/?tag_id=26" target="_blank">2 定义与命题获奖教学课件ppt</a>,文件包含北师大版数学八年级上册72定义与命题第2课时课件pptx、72定义与命题第2课时教案doc、72定义与命题第2课时同步练习docx、72定义与命题第2课时学案docx等4份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
初中数学北师大版八年级上册4 数据的离散程度一等奖教学课件ppt: 这是一份初中数学北师大版八年级上册<a href="/sx/tb_c92970_t3/?tag_id=26" target="_blank">4 数据的离散程度一等奖教学课件ppt</a>,文件包含北师大版数学八年级上册64数据的离散程度第2课时课件pptx、64数据的离散程度第2课时教案doc、64数据的离散程度第2课时同步练习docx、64数据的离散程度第2课时学案docx等4份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
数学八年级上册1 平均数优质教学课件ppt: 这是一份数学八年级上册<a href="/sx/tb_c10063_t3/?tag_id=26" target="_blank">1 平均数优质教学课件ppt</a>,文件包含北师大版数学八年级上册61平均数第2课时课件pptx、61平均数第2课时教案doc、61平均数第2课时同步练习docx、61平均数第2课时学案docx等4份课件配套教学资源,其中PPT共24页, 欢迎下载使用。














