数学八年级上册第5章 一次函数5.3 一次函数同步训练题

这是一份数学八年级上册第5章 一次函数5.3 一次函数同步训练题，文件包含浙教版数学八年级上册第5章一次函数分类专项训练原卷版doc、浙教版数学八年级上册第5章一次函数分类专项训练解析版doc等2份试卷配套教学资源，其中试卷共89页， 欢迎下载使用。
一、单选题
1．（2022·浙江·八年级专题练习）某学校要建一块矩形菜地供学生参加劳动实践，菜地的一边靠墙，另外三边用木栏围成，木栏总长为40m．如图所示，设矩形一边长为xm，另一边长为ym，当x在一定范围内变化时，y随x的变化而变化，则y与x满足的函数关系是（ ）
A．正比例函数关系B．一次函数关系
C．反比例函数关系D．二次函数关系
2．（2022·浙江·杭州市安吉路实验学校八年级期中）已知是直线（a为常数）上的两点，若，则a的值可以是（ ）
A．B．0C．1D．2
3．（2022·浙江·八年级专题练习）若点，，在一次函数（m是常数）的图象上，则的大小关系是（ ）
A． B．C．D．
4．（2022·浙江台州·八年级期末）将直线向上平移2个单位长度，得到的直线为（ ）
A．B．C．D．
5．（2022·浙江·八年级专题练习）将直线向上平移3个单位，得到直线（ ）．
A．y=x﹣3B．y=x+3C．y=3x﹣3D．y=3x+3
6．（2022·浙江·八年级专题练习）若函数是正比例函数，则m值为（ ）
A．3B．-3C．±3D．不能确定
7．（2022·浙江·八年级专题练习）若点在直线上，下列说法不正确的是( )
A．函数y随x的增大而减小B．图象与x轴的交点是(4，0)
C．点一定不在第三象限D．当x＞2时，y＞2
8．（2020·浙江绍兴·八年级期中）在圆周长计算公式中，对半径不同的圆，变量有（ ）
A．B．C．D．
9．（2022·浙江·八年级专题练习）下列函数中是一次函数的是（ ）
A．B．C．D．
10．（2022·浙江金华·八年级期末）已知一次函数y＝kx+b的图象如图所示．当0＜y≤3时，x的取值范围是（ ）
A．x＞-2B．-2≤x≤2C．-2＜x≤0D．x≤0
二、填空题
11．（2022·浙江·八年级专题练习）一个水库的水位在最近5h内持续上涨，水位高度y（m）与时间t（h）之间的函数关系式为，每小时水位上升的高度是______m．
12．（2022·浙江·宁波东海实验学校八年级期中）如果用c表示摄氏温度（），f表示华氏温度（，则c和f之间的关系是：．某日纽约的最高气温为，则换算成摄氏温度为___________．
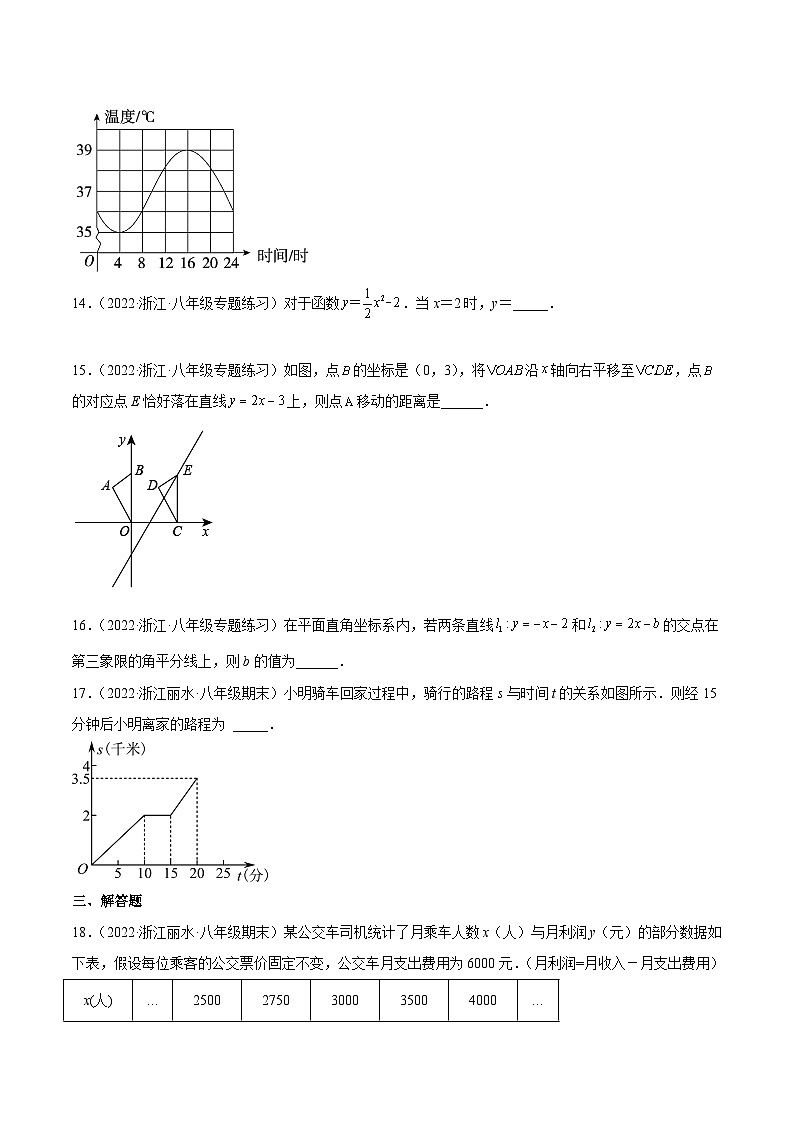
13．（2022·浙江台州·八年级期末）如图是骆驼一天内的体温随时间变化的函数图像，这一天中在_______时间范围内它的体温在上升．
14．（2022·浙江·八年级专题练习）对于函数．当x＝2时，y＝_____．
15．（2022·浙江·八年级专题练习）如图，点的坐标是（0，3），将沿轴向右平移至，点的对应点E恰好落在直线上，则点移动的距离是______．
16．（2022·浙江·八年级专题练习）在平面直角坐标系内，若两条直线和的交点在第三象限的角平分线上，则b的值为______．
17．（2022·浙江丽水·八年级期末）小明骑车回家过程中，骑行的路程s与时间t的关系如图所示．则经15分钟后小明离家的路程为 _____．
三、解答题
18．（2022·浙江丽水·八年级期末）某公交车司机统计了月乘车人数x（人）与月利润y（元）的部分数据如下表，假设每位乘客的公交票价固定不变，公交车月支出费用为6000元．（月利润=月收入－月支出费用）
(1)根据函数的定义，y是关于x的函数吗？
(2)结合表格解答下列问题：
①公交车票的单价是多少元？
②当x=2750时，y的值是多少？它的实际意义是什么？
19．（2022·浙江湖州·八年级期末）已知是关于的一次函数，且当时，；当时，．
(1)求该一次函数的表达式；
(2)当时，求自变量的值．
20．（2022·浙江宁波·八年级期末）为了更好地亲近大自然，感受大自然的美好风光，小聪和小慧去某风景区游览，景区入口与观景点之间的路程为3千米，他们约好在观景点见面．小聪步行先从景区入口处出发，中途休息片刻后继续以原速度前行，此时小慧乘观光车从景区入口处出发，他们沿相同路线先后到达观景点，如图，分别表示小聪与小慧离景区入口的路程y（千米）与小聪离开的时间x（分）之间的关系．根据图像解决下列问题：
(1)小聪步行的速度是______（千米/分），中途休息______分钟；
(2)求小慧离景区入口的路程y（千米）关于小聪离开的时间x（分）的函数表达式；
(3)小慧比小聪早几分钟到达观景点？请说明理由．
21．（2022·浙江湖州·八年级期末）如图，一次函数y＝﹣2x+4的图象分别与x轴、y轴交于点A，B．
（1）求△AOB的面积；
（2）在该一次函数图象上有一点P到x轴的距离为6，求点P的坐标．
22．（2022·浙江舟山·八年级期末）如图，直线y=kx+b经过点A（-5，0），B（-1，4）
（1）求直线AB的表达式；
（2）求直线CE：y=-2x-4与直线AB及y轴围成图形的面积；
（3）根据图象，直接写出关于x的不等式kx+b＞-2x-4的解集．
【典型】
一、单选题
1．（2021·浙江宁波·八年级期末）一根蜡烛长30cm，点燃后每小时燃烧5cm，燃烧时蜡烛剩余的长度h（cm）和燃烧时间t（小时）之间的函数关系用图像可以表示为中的（ ）
A．B．C．D．
2．（2020·浙江杭州·八年级期中）关于一次函数，下列说法正确的是（ ）
A．它的图象过点B．它的图象经过第一、二、三象限
C．随的增大而增大D．当时，总有
3．（2020·浙江杭州·八年级期末）如图是某种产品30天的销售图象，图1是产品日销售量y(件)与时间t(天)的函数关系，图2是一件产品的利润z(元)与时间t(天)的函数关系．则下列结论中错误的是（ ）
A．第24天销售量为300件B．第10天销售一件产品的利润是15元
C．第27天的日销售利润是1250元D．第15天与第30天的日销售量相等
二、填空题
4．（2022·浙江宁波·八年级期末）如图，函数和的图象相交于点，则关于的不等式的解为______．
5．（2020·浙江·宁波市东恩中学八年级阶段练习）函数中自变量x的取值范围是__．
三、解答题
6．（2020·浙江嘉兴·八年级期末）如图，在直角坐标系中，
（1）请写出三个顶点的坐标；
（2）在x轴上找一点P，使的值最小，请在图中表示出点P的位置并写出点P的坐标．
7．（2020·浙江·绍兴市锡麟中学八年级阶段练习）某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中，他们参与了某种水果的销售工作．已知该种水果的进价为8元/千克，下面是他们在活动结束后的对话：
小丽：如果以10元/千克的价格销售，那么每天可售出300 kg．
小强：如果以13元/千克的价格销售，那么每天可获取利润750元．
小红：通过调查验证，我发现每天的销售量y（kg）与销售单价x（元）之间存在一次函数关系．
求y与x（x＞0）之间的函数表达式．
8．（2020·浙江杭州·八年级期末）为进一步普及新观状病毒疫情防控知识，提高学生自我保护能力，时代中学复学后采取了新冠状病毒疫情防控知识竞赛活动，对于成绩突出的同学进行表彰奖励，计划购买甲、乙两种笔记本作为奖品已知3本甲型笔记本和5本乙型笔记本共需50元，2本甲型笔记本和3本乙型笔记本共需31元．
（1）求1本甲型笔记本和1本乙型笔记本的售价各是多少元？
（2）学校准备购买这两种类型的笔记本共200本，要求甲型笔记本的本数不超过乙型笔记本的本数的3倍，请设计出最省钱的购买方案，并求出花费最低的钱数．
【易错】
一．选择题（共5小题）
1．（2022秋•鄞州区校级期中）2022年2月5日，电影《长津湖》在青海剧场首映，小李一家开车去观看．最初以某一速度匀速行驶，中途停车加油耽误了十几分钟，为了按时到达剧场，小李在不违反交通规则的前提下加快了速度，仍保持匀速行驶．在此行驶过程中，汽车离剧场的距离y（千米）与行驶时间t（小时）的函数关系的大致图象是（ ）
A．B．
C．D．
2．（2021秋•东阳市期末）如图①，在△ABC中，∠C＝90°，∠A＝30°，点D是AB边的中点，点P从点A出发，沿着AC﹣CB运动，到达点B停止．设点P的运动路径长为x，连DP，记△APD的面积为y，若表示y与x函数关系的图象如图②所示，则△ABC的周长为（ ）
A．6+2B．4+2C．12+4D．6+4
3．（2021秋•定海区期末）关于一次函数y＝3x﹣1的描述，下列说法正确的是（ ）
A．图象经过第一、二、三象限
B．函数的图象与x轴的交点坐标是（0，﹣1）
C．向下平移 1个单位，可得到y＝3x
D．图象经过点（1，2）
4．（2021秋•余姚市期末）已知不等式ax+b＜0的解是x＞﹣2，下列有可能是函数y＝ax+b的图象的是（ ）
A．B．
C．D．
5．（2021秋•海曙区校级期末）如图，一次函数y＝2x+3与y轴相交于点A，与x轴相交于点B，在直线AB上取一点P（点P不与A，B重合），过点P作PQ⊥x轴，垂足为点Q，连接PO，若△PQO的面积恰好为，则满足条件的P点有（ ）
A．1个B．2个C．3个D．4个
二．填空题（共6小题）
6．（2022秋•南湖区校级期中）若y＝（k﹣1）x+k2﹣1是正比例函数，侧k＝ ．
7．（2021秋•青田县期末）一次函数y＝10﹣2x的比例系数是 ．
8．（2021秋•宁波期末）若一次函数y＝kx+5在﹣1≤x≤4范围内有最大值17，则k＝ ．
9．（2022•下城区校级二模）已知A，B两地相距80km，甲、乙两人沿同一条公路从A地出发到B地，乙骑自行车，甲骑摩托车．图中DE，OC分别表示甲、乙离开A地的路程s（km）与时间t（h）的函数关系的图象，则甲与乙的速度之差为 ，甲出发后经过 小时追上乙．
10．（2021秋•开化县期末）如图1，在Rt△ABC中，∠C＝90°，点P从点C出发，沿三角形的边以1cm/秒的速度顺时针运动一周，点P运动时线段CP的长度y（cm）随运动时间x（秒）变化的关系如图2所示，若点M的坐标为（11，5），则点P运动一周所需要的时间为 秒．
11．（2022秋•鄞州区校级期中）已知直线y1＝x，y2＝x+1，y3＝﹣x+6，若无论x取何值，y总取y1、y2、y3中的最小值，则y的最大值为 ．
三．解答题（共5小题）
12．（2021秋•上城区期末）设两个不同的一次函数y1＝ax+b，y2＝bx+a（a，b是常数，且ab≠0）．
（1）若函数y1的图象经过点（2，1），且函数y2的图象经过点（1，2），求a，b的值；
（2）写出一组a，b的值，使函数y1、y2图象的交点在第四象限，并说明理由；
（3）已知a＝1，b＝﹣1，点A（p，m）在函数y1的图象上，点B（q，n）在函数y2的图象上，若p+q＝2，判断m和n的大小关系．
13．（2021秋•德清县期末）甲、乙两人分别从同一公路上的A，B两地同时出发骑车前往C地，两人离A地的距离y（km）与甲行驶的时间x（h）之间的关系如图所示，请根据图象所提供的信息解答下列问题：
（1）A，B两地相距 km；乙骑车的速度是 km/h；
（2）请分别求出甲、乙两人在0≤x≤6的时间段内y与x之间的函数关系式；
（3）求甲追上乙时用了多长时间．
14．（2021秋•余姚市期末）已知甲、乙两物体沿同一条直线同时、同向匀速运动，它们所经过的路程s与所需时间t之间的函数表达式分别为s＝v1t+a1和s＝v2t+a2，图象如图所示．
（1）哪个物体运动得快一些？从物体运动开始，2秒以前谁先谁后？
（2）根据图象确定何时两物体处于同一位置？
（3）求v1，v2的值，并写出两个函数表达式．
15．（2021秋•吴兴区期末）如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点B，过点B的直线交x轴正半轴于C，且△ABC的面积为56．点D为线段AB的中点，点E为y轴上一动点，连接DE，将线段DE绕着点E逆时针旋转90°得到线段EF，连接DF．
（1）求点C的坐标及直线BC的表达式；
（2）在点E运动的过程中，若△DEF的面积为5，求此时点E的坐标；
（3）设点E的坐标为（0，m）；
①用m表示点F的坐标；
②在点E运动的过程中，若△DEF始终在△ABC的内部（包括边界），直接写出满足条件的m的取值范围．
16．（2021秋•慈溪市期末）甲、乙两同学住在同一小区，是某学校的同班同学，小区和学校在一笔直的大街上，距离为2560米，在该大街上，小区和学校附近各有一个公共自行车取（还）车点．甲从小区步行去学校，乙比甲迟出发，步行到取车点后骑公共自行车去学校，到学校旁还车点后立即步行到学校（步行速度不变，不计取还车的时间）．设甲步行的时间为x（分），图1中的线段OM和折线P一Q一R一T分别表示甲、乙同学离小区的距离y（米）与x（分）的函数关系的图象；图2表示甲、乙两人的距离s（米）与x（分）的函数关系的图象（一部分）．根据图1、图2的信息，解答下列问题：
（1）分别求甲、乙两同学的步行速度与乙骑自行车的速度；
（2）求乙同学骑自行车时，y与x的函数关系式和a的值；
（3）补画完整图2，并用字母标注所画折线的终点及转折点，写出它们的坐标．
【压轴】
一、解答题
1．（2022·浙江·八年级专题练习）如图，已知点A（0，6），点C（3，0），将线段AC绕点C顺时针旋转，点A落在点B处，点D是x轴上一动点．
(1)求直线BC的解析式；
(2)联结B、D．若，求点D的坐标；
(3)联结A、D交线段BC于点Q，且∠OAC＝∠CAQ．求△BCD的面积．
2．（2022·浙江丽水·八年级期末）已知，一次函数y=x＋4的图象与x轴、y轴分别交于点A，点B，点C的坐标为（－2，0）．
(1)求点A，点B的坐标；
(2)过点C作直线CD，与AB交于点D，且，求点D的坐标；
(3)连接BC，将△OBC沿x轴向左平移得到△O′B′C′，再将以A，B，B′，C′为顶点的四边形沿O′B′剪开得到两个图形．若用这两个图形拼成不重叠且无缝隙的图形恰好是三角形，求△OBC平移的距离．
3．（2022·浙江·八年级专题练习）【探索发现】如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线DE经过点C，过A作AD⊥DE于点D．过B作BE⊥DE于点E，则△BEC≌△CDA，我们称这种全等模型为“k型全等”．（不需要证明）
【迁移应用】已知：直线y＝kx＋3（k≠0）的图象与x轴、y轴分别交于A、B两点．
(1)如图2. 当时，在第一象限构造等腰直角△ABE，；
①直接写出OA＝ ，OB＝ ；
②求点E的坐标；
(2)如图3，当k的取值变化，点A随之在x轴负半轴上运动时，在y轴左侧过点B作BN⊥AB，并且BN＝AB，连接ON，问△OBN的面积是否为定值，请说明理由；
(3)【拓展应用】如图4，当时，直线与y轴交于点D，点P（n，－2）、Q分别是直线l和直线AB上的动点，点C在x轴上的坐标为（3，0），当△PQC是以CQ为斜边的等腰直角三角形时，求点Q的坐标．
4．（2022·浙江·杭州市十三中教育集团（总校）八年级开学考试）设函数y1＝ax+b，y2＝bx+a（a，b为常数，ab≠0且a≠b），函数y1和y2的图象的交点为点P．
(1)求点P的横坐标．
(2)已知点P在第一象限，函数y2的值随x的增大而增大．
①当x＝2时，y2﹣y1＝2，求a的取值范围．
②若点P的坐标是（1，1），且a＞b，求证：当x＝2时，y1﹣y2＜
5．（2022·浙江·八年级专题练习）【模型建立】
（1）如图1，等腰RtABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过点A作AD⊥ED于点D，过点B作BE⊥ED于点E，求证：BEC≌CDA．
【模型应用】
（2）如图2，已知直线l1：y＝x+3与x轴交于点A，与y轴交于点B，将直线l1绕点A逆时针旋转45°至直线l1则直线l2的函数表达式为 ．
（3）如图3，将图1四边形放到平面直角坐标系中，点E与O重合，边ED放到x轴上，若OB＝2，OC＝1，在x轴上存在点M使的以O、A、B、M为顶点的四边形面积为4，请直接写出点M的坐标 ．
（4）如图4，平面直角坐标系内有一点B(3，﹣4)，过点B作BA⊥x轴于点A，BC⊥y轴于点C，点P是线段AB上的动点，点D是直线y＝﹣2x+1上的动点且在第四象限内．若CPD是等腰直角三角形．请直接写出点D的坐标．
6．（2021·浙江·义乌市绣湖中学教育集团八年级阶段练习）（1）模型建立，如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于D，过B作BE⊥ED于E．求证：△BEC≌△CDA；
（2）模型应用：
①已知直线y＝x+3与y轴交于A点，与x轴交于B点，将线段AB绕点B逆时针旋转90度，得到线段BC，过点A，C作直线，求直线AC的解析式；
②如图3，矩形ABCO，O为坐标原点，B的坐标为(8，6)，A，C分别在坐标轴上，P是线段BC上动点，已知点D在第一象限，且是直线y＝2x﹣5上的一点，若△APD是不以A为直角顶点的等腰直角三角形，请直接写出所有符合条件的点D的坐标．
7．（2021·浙江温州·八年级期中）如图1，在平面直角坐标系中，直线与坐标轴交于A，B两点，点C为AB的中点，动点P从点A出发，沿AO方向以每秒1个单位的速度向终点O运动，同时动点Q从点O出发，以每秒2个单位的速度沿射线OB方向运动，当点P到达点O时，点Q也停止运动．以CP，CQ为邻边构造CPDQ，设点P运动的时间为t秒．
(1)直接写出点C的坐标______．
(2)如图2，过点D作轴，过点C作轴．证明：．
(3)如图3，连接OC，当点D恰好落在的边所在的直线上时，求所有满足要求的t的值．
8．（2021·浙江·八年级期中）如图1，已知一次函数的图象分别交y轴正半轴于点A，x轴正半轴于点B，且的面积是24，P是线段上一动点．
（1）求k值；
（2）如图1，将沿翻折得到，当点正好落在直线上时，
①求点的坐标；
②将直线绕点P顺时针旋转得到直线，求直线的表达式；
（3）如图2，上题②中的直线与线段相交于点M，将沿着射线向上平移，平移后对应的三角形为，当是以为直角边的直角三角形时，请直接写出点的坐标．
x(人)
…
2500
2750
3000
3500
4000
…
y（元）
…
－1000
－500
0
1000
2000
…