






人教B版 (2019)选择性必修 第一册2.5.1 椭圆的标准方程背景图ppt课件
展开
这是一份人教B版 (2019)选择性必修 第一册2.5.1 椭圆的标准方程背景图ppt课件,共20页。PPT课件主要包含了情景与问题,尝试与发现,椭圆的标准方程,焦点在x轴,焦点在y轴等内容,欢迎下载使用。
日常生活中,可以见到很多有关椭圆的形象。我们知道,圆是平面内到圆心的距离等于半径的点的集合,圆上的点的特征是:任意一点到圆心的距离都等于半径.那么,你能说说到底什么是椭圆吗?椭圆上任意一点的特征是什么?
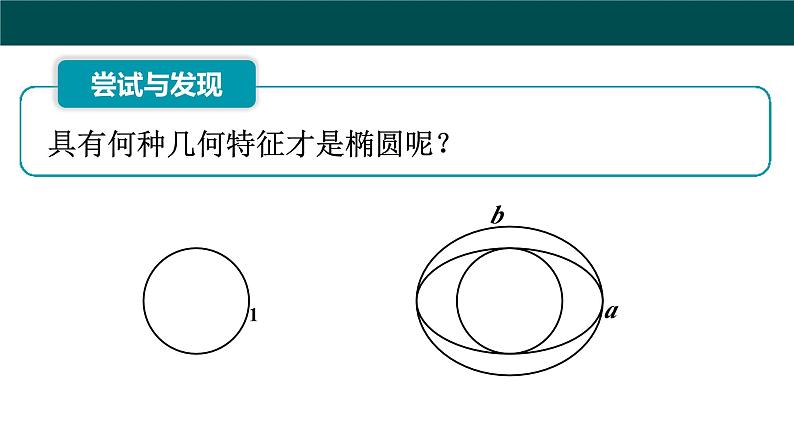
具有何种几何特征才是椭圆呢?
我们把平面内与两个定点F1,F2的距离的和等于常数2a(大于|F1F2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,
两焦点间的距离叫做椭圆的焦距,
焦距的一半称为半焦距.
|PF1|+|PF2|=2a > |F1F2|
若|PF1|+|PF2|=2a = |F1F2|或|PF1|+|PF2|=2a 0)
则F1(-c,0),F2(c,0)
根据椭圆定义,设|MF1|+|MF2|=2a
你可以在图中找出表示a,c,b的线段吗?
当焦点F1,F2在y轴上时,椭圆的方程是什么?
其中,a>b>0,且a2=b2+c2
焦点F1(0,-c),F2(0,c)
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
(-a,0) (a,0)(0,-b) (0,b)
(0,-a) (0,a)(-b,0) (b,0)
a>b>0,且a2=b2+c2
例1. 平面内有一长度为4的线段AB,动点P满足|PA|+|PB|=6,则点P的轨迹是()A.直线B.射线C.椭圆D.圆
例3 已知B,C是平面内的两个定点,|BC|=8,且平面内ΔABC的周长等于18,求这个三角形的顶点A的轨迹方程.
分析:由ΔABC的周长等于18且|BC|=8,可知点A到B,C两个定点的距离之和总是等于10,因此点A一定在以B,C为焦点的椭圆上。
椭圆:我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
|PF1|+|PF2|=2a > 2c
相关课件
这是一份人教B版 (2019)2.6.1 双曲线的标准方程背景图课件ppt,共18页。PPT课件主要包含了可口可乐的下半部,玉枕的形状,情景与问题,这两个定点叫做焦点,常数2a2c,不存在,一条射线,两条射线,双曲线,双曲线的一支等内容,欢迎下载使用。
这是一份高中数学人教B版 (2019)选择性必修 第一册2.6.1 双曲线的标准方程备课课件ppt,共21页。PPT课件主要包含了情境与问题,尝试与发现,动画演示,求双曲线的标准方程等内容,欢迎下载使用。
这是一份数学人教B版 (2019)2.5.1 椭圆的标准方程评课ppt课件,共20页。PPT课件主要包含了学习任务,主体学习,情境与问题,尝试与发现,课堂小结等内容,欢迎下载使用。









