数学八年级上册第15章 轴对称图形和等腰三角形15.3 等腰三角形试讲课课件ppt

这是一份数学八年级上册第15章 轴对称图形和等腰三角形15.3 等腰三角形试讲课课件ppt，共35页。PPT课件主要包含了几何语言，归纳总结，巩固练习，不一定是等内容，欢迎下载使用。

等腰三角形的两个底角相等.
等腰三角形顶角的平分线垂直平分底边
① 等边三角形三个内角相等，每一个内角都等于60°.
② 等边三角形各边上的高、中线和所对角的平分线都“三线合一”
③ 等边三角形是特殊的等腰三角形，具备等腰三角形的所有性质.
等腰三角形中常见的添辅助线的方法是： 作等腰三角形的顶角平分线、底边上的中线和底边上的高.
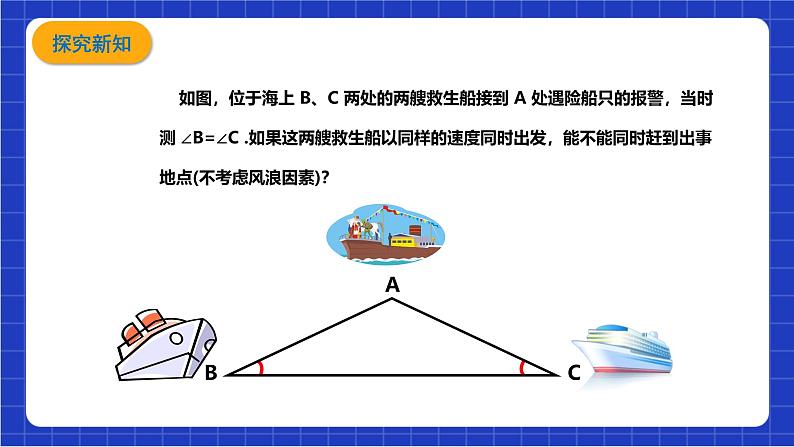
如图，位于海上 B、C 两处的两艘救生船接到 A 处遇险船只的报警，当时测 ∠B=∠C .如果这两艘救生船以同样的速度同时出发，能不能同时赶到出事地点(不考虑风浪因素)？
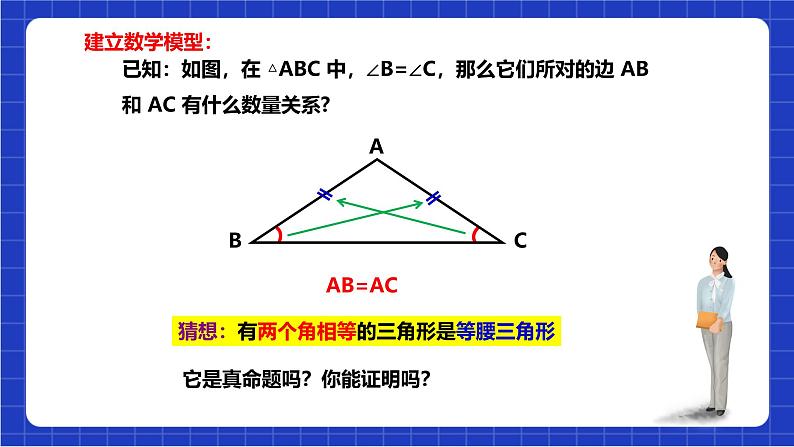
已知：如图，在 △ABC 中，∠B=∠C，那么它们所对的边 AB 和 AC 有什么数量关系?
猜想：有两个角相等的三角形是等腰三角形
它是真命题吗？你能证明吗？
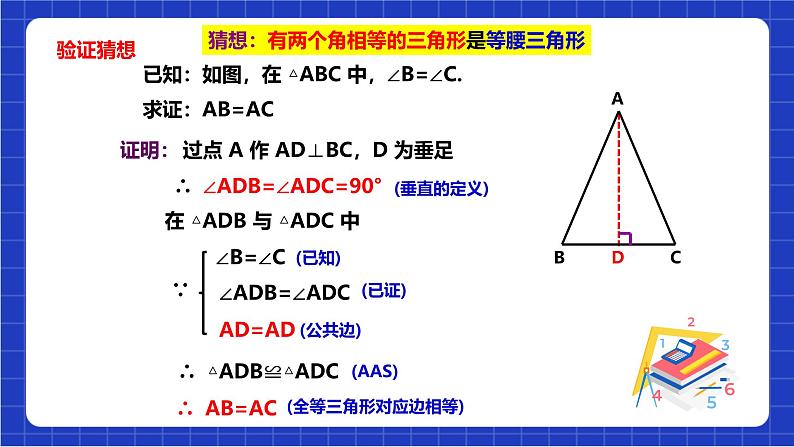
已知：如图，在 △ABC 中，∠B=∠C.
过点 A 作 AD⊥BC，D 为垂足
∴ ∠ADB=∠ADC=90°
在 △ADB 与 △ADC 中
∴ △ADB≌△ADC
(全等三角形对应边相等)
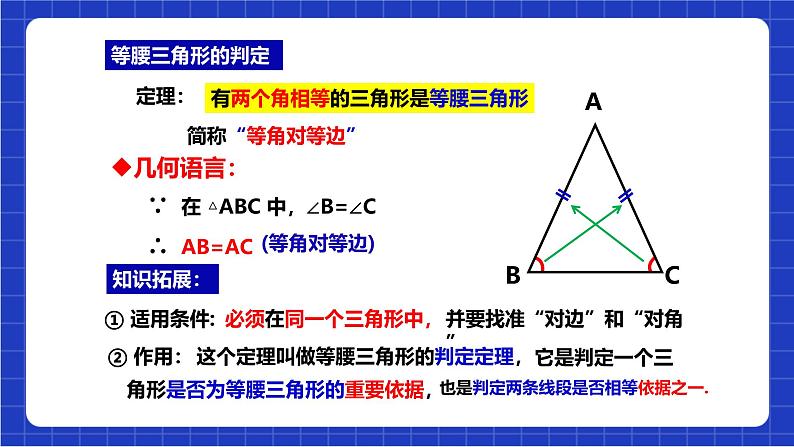
有两个角相等的三角形是等腰三角形
∵ 在 △ABC 中，∠B=∠C
必须在同一个三角形中，
并要找准“对边”和“对角”
它是判定一个三角形是否为等腰三角形的重要依据，
这个定理叫做等腰三角形的判定定理，
也是判定两条线段是否相等依据之一.
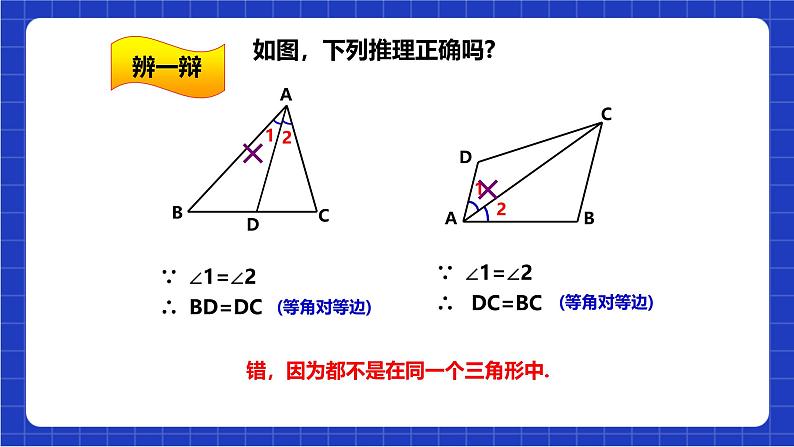
如图，下列推理正确吗?
错，因为都不是在同一个三角形中.
∵ ∠1=∠2 ∴ BD=DC
∵ ∠1=∠2 ∴ DC=BC
思考：等腰三角形的性质与判定的相同点和不同点：
使用的前提都是“在同一个三角形中”
由三角形的两边相等，得到它们所对的角相等，是等腰三角形的性质.
由三角形的两角相等，得到它们所对的边相等，是等腰三角形的判定.
1、如图，关于△ABC，给出下列四组条件： ① △ABC 中，AB=AC； ② △ABC 中，∠B=56°，∠BAC=68°； ③ △ABC 中，AD⊥BC，AD 平分 ∠BAC； ④ △ABC 中，AD⊥BC，AD 平分边 BC．其中，能判定 △ABC 是等腰三角形的条件共有（　　） A.1组 B.2组 C.3组 D.4组
判定一个三角形是否为等腰三角形的方法有几种?
① 有两条边相等的三角形是等腰三角形
② 有两个角相等的三角形是等腰三角形，即“等角对等边”
(等腰三角形的判定定理)
2、已知：如图，四边形ABCD中，AB＝AD，∠B＝∠D. 求证：BC＝CD.
∴ ∠ABD=∠ADB
又∵ ∠ABC=∠ADC
∴ ∠ABC-∠ABD=∠ADC-∠ADB
即 ∠DBC=∠BDC
3、如图，已知在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD与CE相交于M点。求证：BM=CM.
∴ ∠ABC=∠ACB
∴ BD⊥AC，CE⊥AB
∴ ∠BEC=∠CDB=90°
∴ ∠1+∠ACB=90°
(直角三角形两个锐角互余)
∠2+∠ABC=90°
4、如图，AE 是 △ABC 的外角 ∠DAC 的平分线，且 AE∥ BC.请你判断 △ABC 的形状，并说明理由.
解：△ABC 是等腰三角形.
∵ AE是 ∠DAC 的平分线
∴ ∠DAE=∠EAC
(两直线平行，同位角相等)
(两直线平行，内错角相等)
∴ △ABC 是等腰三角形
“角平分线+平行线 等腰三角形”是一种常见的基本图形
思考 1：如何判断一个三角形是不是等边三角形？
猜想：三个角都相等的三角形是等边三角形.
已知：如图，△ABC 中， ∠ A=∠B=∠C
求证：△ABC 是等边三角形
∴ △ABC是等边三角形
三个角都相等的三角形是等边三角形.
∵ 在 △ABC 中，∠A=∠B=∠C
∴ △ABC 是等边三角形
(三个角都相等的三角形是等边三角形)
思考 2：如果一个等腰三角形中有一个角是 60°，那么这个三角形是什么三角形？
① 当顶角是 60° 时
② 当底角是 60° 时
已知：△ABC中，AB=AC， ∠A=60°.求证：△ABC是等边三角形
= ×(180°-∠A）
∴ ∠A=∠B=∠C= 60°
已知：△ABC中，AB=AC， ∠B=60°.求证：△ABC是等边三角形
∴ ∠A=180°-∠B-∠C= 60°
有一个角是 60° 的等腰三角形是等边三角形.
∵ 在 △ABC 中，AB=AC，∠A=60°
(有一个角是 60° 的等腰三角形是等边三角形)
1、根据条件判断下列三角形是否为等边三角形.
判定一个三角形是否为等边三角形的方法有几种？
① 若已知三边关系，则考虑用“三条边都相等的三角形是等边 三角形”判定.
② 若已知三角关系，则考虑用“三个角都相等的三角形是等边 三角形”判定.
③ 若已知该三角形是等腰三角形，则根据“有一个角是 60° 的 等腰三角形是等边三角形”判定.
(等边三角形的判定 1 )
(等边三角形的判定 2 )
2、如图，在等边三角形 ABC 中，DE∥ BC. 求证：△ADE 是等边三角形.
∵ △ABC 是等边三角形
∴ ∠A=∠B= ∠C
∴ ∠ADE=∠B，∠AED=∠C
∴ ∠A=∠ADE= ∠AED
∴ △ADE 是等边三角形
　解：成立.理由如下： ∵ △ABC 是等边三角形， ∴ ∠A =∠ABC =∠ACB ∵ DE∥ BC ∴ ∠ABC =∠ADE ∠ACB =∠AED ∴ ∠A =∠ADE =∠AED. ∴ △ADE 是等边三角形.
变式 1　若点D、E 在边AB、AC 的延长线上，且 DE∥ BC，结论还成立吗？
变式 2 若点 D、E 在边 AB、AC 的反向延长线上，且 DE∥ BC， 结论依然成立吗？
　　解： 成立.理由如下： ∵ △ABC 是等边三角形 ∴ ∠BAC =∠B =∠C ∵ DE∥ BC ∴ ∠B =∠D，∠C =∠E 又∵ ∠EAD=∠BAC ∴ ∠EAD =∠D =∠E ∴ △ADE 是等边三角形
等边三角形任意一边的平行线与另外两边或两边延长线相交所构成的三角形是等边三角形.
3、如图，△ABC 为等边三角形，点 D，E，F 分别在 BC，CA，AB 上，且 AF=BD=CE. 求证：△DEF 是等边三角形.
∵ △ABC是等边三角形
∴ AB=AC=BC，
∴ AC-CE=BC-BD
在△AEF和△CDE中
∴ △AEF≌△CDE
∴ △DEF是等边三角形
∠A=∠B=∠C=60°
(三条边都相等的三角形是等边三角形)
4、如图，△ABC为等边三角形，点 P 在 △ABC 内，点 Q 在△ABC 外，点 B，P，Q 在同一条直线上，且 ∠ABP=∠ACQ，BP=CQ.(1) 求证：△ABP≌△ACQ；(2) 请判断 △APQ 是什么形状的三角形？试说明理由.
5、如图，点 C 为线段 AB 上一点，△ACM，△CBN 是等边三角形，AN、MC 交于点 E， BM、CN 交于点 F. 求证： (1) AN=BM； (2) △CEF 是等边三角形. (3) EF∥ AB
1、如图，在 △ABC 中，AB=AC，EF 交 AB 于点 E，交 BC 与点 D．交 AC 的延长线于点 F，且 BE=CF．求证：DE=DF
利用平行线构造等腰三角形：
等腰三角形任意一边的平行线与另外两边相交所构成的三角形是等腰三角形.
过点 E 作 EG∥ AC 交 BC 于 G ，
则 ∠ACB=∠BGE，
在 △CDF 和 △GDE 中
∴ △CDF≌△GDE (AAS)
2、如图 1，△ABC 中，∠ABC、∠ACB 的平分线交于 O 点，过 O 点作 BC 平行线交 AB、AC 于 D、E．(1) 请写出图1中线段BD，CE，DE之间的数量关系？并说明理由.
2、如图 1，△ABC 中，∠ABC、∠ACB 的平分线交于 O 点，过 O 点作 BC 平行线交 AB、AC 于 D、E． (2) 如图 2，△ABC 若 ∠ABC 的平分线与 △ABC 的外角平分线交于 O，过点 O 作 BC 平行线交 AB 于 D，交 AC 于 E．那么 BD，CE，DE 之间存在什么数量关系？并证明这种关系.
2、如图 1，△ABC 中，∠ABC、∠ACB 的平分线交于 O 点，过 O 点作 BC 平行线交 AB、AC 于 D、E． (3) 若将图 1 中两个内角的角平分线改为两个都是外角 (如图3，∠DBC、∠BCE) 的角平分线，其它条件不变，那么 BD，CE，DE之间存在什么数量关系？请直接写出你的猜想(不需证明).
3、A、B 是 4×4 网格中的格点，网格中的每个小正方形的边长为 1，请在图中清晰标出使以 A、B、C 为顶点的三角形是等腰三角形的所有格点 C 的位置．
分别以 A、B、C 为顶角顶点来分类讨论！
4、如图，直线 a、b 相交于点 O，∠1=50°，点 A 在直线 a 上，直线 b 上存在点 B，使以点 O、A、B 为顶点的三角形是等腰三角形，这样的B点有（　　） A．1个 B．2个 C．3个 D．4个