2020-2021学年15.3 等腰三角形课文内容ppt课件

这是一份2020-2021学年15.3 等腰三角形课文内容ppt课件，共43页。PPT课件主要包含了新课导入，讲授新课，当堂练习，课堂小结等内容，欢迎下载使用。

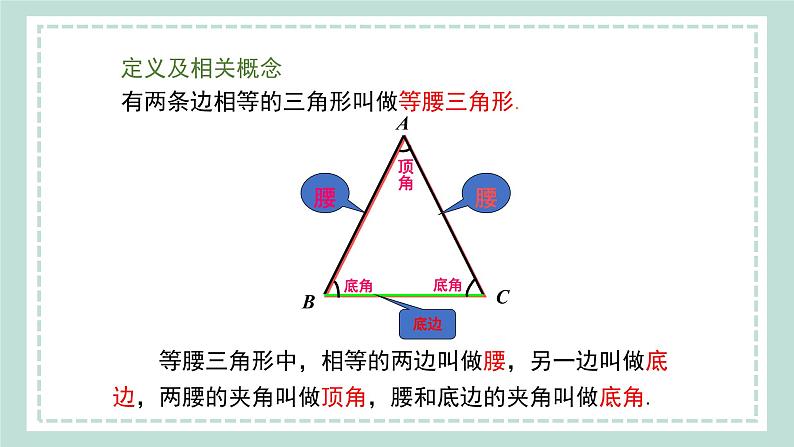
定义及相关概念有两条边相等的三角形叫做等腰三角形.
等腰三角形中，相等的两边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.
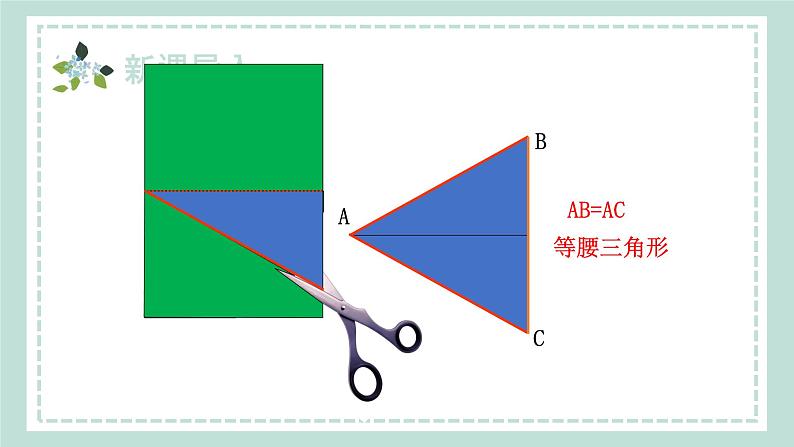
剪一剪：把一张长方形的纸按图中的红线对折，并剪去阴影部分（一个直角三角形），再把得到的直角三角形展开，得到的三角形ABC有什么特点？
等腰三角形的边角性质：等边对等角
折一折：△ABC 是轴对称图形吗？它的对称轴是什么？
折痕所在的直线是它的对称轴.
找一找：把剪出的等腰三角形ABC沿折痕对折，找出其中重合的线段和角.
等腰三角形是轴对称图形.
猜一猜： 由这些重合的角，你能发现等腰三角形的性质吗？
定理1 等腰三角形的两个底角相等（等边对等角）.
已知：△ABC 中，AB=AC,求证：∠B=∠C .
应用格式：∵AB=AC（已知） ∴∠B=∠C（等边对等角）
证法2：作顶角∠BAC的平分线AD，交BC于点D. ∵AD平分∠BAC ， ∴∠1＝∠2. 在△ABD与△ACD中，AB＝AC（已知），∠1＝∠2（已证）， AD＝AD（公共边），∴ △ABD ≌ △ACD（SAS），∴ ∠B＝∠C.
证法3：作底边BC的高AD，交BC于点D. ∵AD⊥BC， ∴ ∠ADB ＝∠ADC＝90°. 在Rt△ABD与Rt△ACD中， AB＝AC（已知）， AD＝AD（公共边），∴ Rt△ABD ≌ Rt△ACD（HL）， ∴ ∠B＝∠C.
解 :∵AB=AC,（已知）∴∠B=∠C，（等边对等角）∴∠B=∠C= ×(180°－120°)=30°.又∵BD=AD,（已知）∴∠BAD=∠B=30°.（等边对等角）同理，∠CAE=∠C=30°.∴∠DAE=∠BAC-∠BAD-∠CAE =120°-30°-30°=60°.
如图，在ΔABC中，AB=AC,∠BAC=120°， 点D, E是底边上两点，且BD=AD,CE=AE. 求∠DAE的度数.
（2）设∠A=x,请把△ ABC的内角和用含x的式子表示出来.
如图，在△ABC中 ，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数.
解析：（1）观察∠BDC与∠A、∠ABD的关系，∠ABC、∠C呢？
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠C= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A.
∵ ∠A+ ∠ABC+ ∠ C=180 °,∴x+2x+2x=180 °,
解：∵AB=AC，BD=BC=AD，∴∠ABC=∠C=∠BDC， ∠A=∠ABD.设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,从而∠ABC= ∠C= ∠BDC=2x,于是在△ABC中，有∠A+∠ABC+∠C=x+2x+2x=180 ° ，解得 x=36 ° ，在△ABC中， ∠A=36°，∠ABC=∠C=72°.
方法总结：利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系，当这种等量关系或和差关系较多时，可考虑列方程解答，设未知数时，一般设较小的角的度数为x.
【变式题】如图，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度数.
解：∵AB=AD=DC， ∴ ∠B= ∠ADB，∠C= ∠DAC. 设 ∠C=x，则 ∠DAC=x， ∠B= ∠ADB= ∠C+ ∠DAC=2x. 在△ABC中， 根据三角形内角和定理得 2x+x+26°+x=180°， 解得x=38.5°. ∴ ∠C= x=38.5°， ∠B=2x=77°.
等腰三角形的一个内角是50°，求这个三角形的底角的度数.
解：当50°的角是底角时，三角形的底角就是50°；当50°的角是顶角时，两底角相等，根据三角形的内角和定理易得底角是65°.
方法总结：等腰三角形的两个底角相等，已知一个内角，则这个角可能是底角也可能是顶角，要分两种情况讨论．
求证：斜边和一直角边分别相等的两个直角三角形全等．已知，如图，在Rt△ABC和Rt△A'B'C'中，∠C=∠C'=90°，AB=A'B'，AC=A'C'求证：Rt△ABC≌Rt△A'B'C'.
本例是14.2中以学过的判定两个直角三角形全等的定理“HL”的证明
证明：在平面内移动Rt△ABC和Rt△A'B'C'，使点A和A'、点C和C'重合，点B和点B'在AC两侧，如图
∵∠BCB'=90°+90°=180°，（等式的性质）∴B,C,B'三点在一条直线上.（平角的定义）在△ABB'中，∵AB=AB',（已知）∴∠B=∠B'.（等角对等边）在Rt△ABC和Rt△A'B'C'中， ∠ACB=∠A'C'B'，（已知） ∠B=∠B'，（已证） AB=A'B'，（已知）∴Rt△ABC≌Rt△A'B'C'.（AAS）
等腰三角形的轴对称性：“三线合一”
等腰三角形的轴对称性：“三线合一”定理2：等腰三角形顶角的平分线垂直平分底边．结论：等腰 三角形顶角的平分线、底边上的中线、底边上的高相 互重合(简称“三线合一”)．要点精析：(1)含义：这是等腰三角形所特有的性质，它实际是 一组定理，应用过程中，在三角形是等腰三角形前提下， “顶角的平分线、底边上的中线、底边上的高”只要知道其 中“一线”，就可以说明是其他“两线”．(2)作用：是证明线段相等、角相等、垂直等关系的重要方法， 应用广泛．
(3)对称性：等腰三角形是轴对称图形，顶角平分线(或底边上 的高、底边上的中线)所在的直线是它的对称轴．(4)应用格式：如图，在△ABC中， ①∵AB＝AC，AD⊥BC，∴AD平分∠BAC(或BD＝CD)； ②∵AB＝AC，BD＝DC，∴AD⊥BC(或AD平分∠BAC)； ③∵AB＝AC，AD平分∠BAC，∴BD＝DC(或AD⊥BC)．
如图，在△ABC中，AB＝AC，AD是BC边上的中线， ∠ABC的平分线BG交AC于点G，交AD于点E， EF⊥AB，垂足为F. (1)若∠BAD＝25°，求∠C的度数； (2)求证：EF＝ED.解： (1) ∵AB＝AC，AD是BC边上的中线， ∴∠BAD＝∠CAD， ∴∠BAC＝2∠BAD＝50°. ∵AB＝AC， ∴ ∠C＝∠ABC＝
证明： (2) ∵AB＝AC，AD是BC边上的中线， ∴AD⊥BC，∴∠BDE＝90°. ∵EF⊥AB， ∴∠BFE＝90°，∴∠BFE＝∠BDE. 又∵BG平分∠ABC， ∴∠FBE＝∠DBE. ∵BE为公共边， ∴△BDE≌△BFE， ∴EF＝ED.
等腰三角形“三线合一”的性质是证明角相等、线段相等和垂直关系的既重要又简便的方法；因为题目的证明或计算所求结果大多都是单一的，所以“三线合一”的性质的应用也是单一的，一般得出一个结论，因此应用要灵活．在等腰三角形中，作“三线”中“一线”，利用“三线合一”是等腰三角形中常用的方法．
如图所示，AB＝AE，BC＝DE，∠B＝∠E， AM⊥CD， 垂足为M.求证：CM＝MD. 导引：由已知AM⊥CD和结论CM＝MD，联想到等腰三角形“三 线合一”的性质，由此连接AC，AD构造等腰三角形． 证明：如图，连接AC，AD. 在△ABC和△AED中， ∴△ABC≌△AED(SAS)．∴AC＝AD. 又∵AM⊥CD，∴CM＝MD.
1.等腰三角形的顶角一定是锐角.2.等腰三角形的底角可能是锐角或者直角、 钝角都可以.3.钝角三角形不可能是等腰三角形. 4.等腰三角形的顶角平分线一定垂直底边.5.等腰三角形的角平分线、中线和高互相重合.6.等腰三角形底边上的中线一定平分顶角.
问题1 等边三角形的三个内角之间有什么关系？
∠A=∠B=∠C=60°
等腰三角形的性质定理的推论
推论： 等边三角形的三个内角都相等，并且每一 个角都等于60°.
已知：AB=AC=BC ， 求证：∠A= ∠ B=∠C= 60°.
证明： ∵AB=AC. ∴∠B=∠C .(等边对等角) 同理 ∠A=∠C . ∴∠A=∠B=∠C. ∵ ∠A+∠B+∠C=180°, ∴ ∠A= ∠B= ∠C=60 °.
问题2 等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴？
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高底边的中线三线合一
如图，△ABC是等边三角形，E是AC上一点，D是BC延长线上一点，连接BE，DE，若∠ABE＝40°，BE＝DE，求∠CED的度数．
解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°.∵∠ABE＝40°，∴∠EBC＝∠ABC－∠ABE＝60°－40°＝20°.∵BE＝DE， ∴∠D＝∠EBC＝20°，∴∠CED＝∠ACB－∠D＝40°.
方法总结：等边三角形是特殊的三角形，它的三个内角都是60°，这个性质常应用在求三角形角度的问题上，一般需结合”等边对等角”、三角形的内角和与外角的性质.
如图，△ABC是等边三角形，BD平分∠ABC，延长BC到E，使得CE=CD．求证：BD=DE．
证明：∵△ABC是等边三角形，BD是角平分线，∴∠ABC=∠ACB=60°．∠DBC=30°（等腰三角形三线合一）．又∵CE=CD，∴∠CDE=∠CED．又∵∠BCD=∠CDE+∠CED，∴∠CDE=∠CED=30°．∴∠DBC=∠DEC．∴DB=DE（等角对等边）．
2.如图，在△ABC中，AB=AC，过点A作AD∥BC，若∠1=70°，则∠BAC的大小为（　　）A．40° B．30° C．70° D．50°
1.等腰三角形有一个角是90°，则另两个角分别是(　　)A．30°，60° B．45°，45° C．45°，90° D．20°，70°
3.(1)等腰三角形一个底角为75°,它的另外两个角为____ __；(2)等腰三角形一个角为40°,它的另外两个角为____________________；(3)等腰三角形一个角为120°,它的另外两个角为_ ___ __.
70°,70°或40°,100°
4.在△ABC中， AB=AC，AB的垂直平分线与AC所在的直线相交得的锐角为50°，则底角的大小为___________．
注意：当题目为给定三角形的形状时，一般需分锐角三角形和钝角三角形两种情况进行分类讨论.
5.如图，在△ABC中，AB = AC，D是BC边上的中点， ∠B = 40°，求 ∠BAD 和 ∠ADC的度数.
解：∵AB=AC，D是BC边上的中点，
∴ ∠C= ∠ B=40°，∠BAD = ∠ DAC，∠ADC = 90°.
∴∠ BAC =180° - 40°-40° = 100°.
6.如图，已知△ABC为等腰三角形，BD、CE为底角的平分线，且∠DBC＝∠F，求证：EC∥DF.
∴∠DBC＝∠ECB.∵∠DBC＝∠F，∴∠ECB＝∠F，∴EC∥DF.
证明：∵△ABC为等腰三角形，AB＝AC，
∴∠ABC＝∠ACB.
又∵BD、CE为底角的平分线，
7. △ABC为正三角形，点M是BC边上任意一点，点N是CA边上任意一点，且BM＝CN，BN与AM相交于Q点，∠BQM 等于多少度？
解：∵△ABC为正三角形，∴∠ABC＝∠C＝∠BAC＝60°，AB＝BC.又∵BM＝CN，∴△AMB≌△BCN(SAS)，∴∠BAM＝∠CBN，∴∠BQM＝∠ABQ＋∠BAM ＝∠ABQ＋∠CBN＝∠ABC＝60°.
8.A、B是4×4网格中的格点，网格中的每个小正方形的边长为1，请在图中清晰标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置．
分别以A、B、C为顶角顶点来分类讨论！
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
等边三角形三个内角相等，且均等于60°