数学4.1 平方根试讲课ppt课件

这是一份数学4.1 平方根试讲课ppt课件，共29页。PPT课件主要包含了x2＝a等内容，欢迎下载使用。

1. 了解平方根的概念，会用符号正确地表示非负数的平方根；
2. 了解开平方运算和平方运算之间的互逆关系，会求某些非负数的平方根，发展逆向思维.
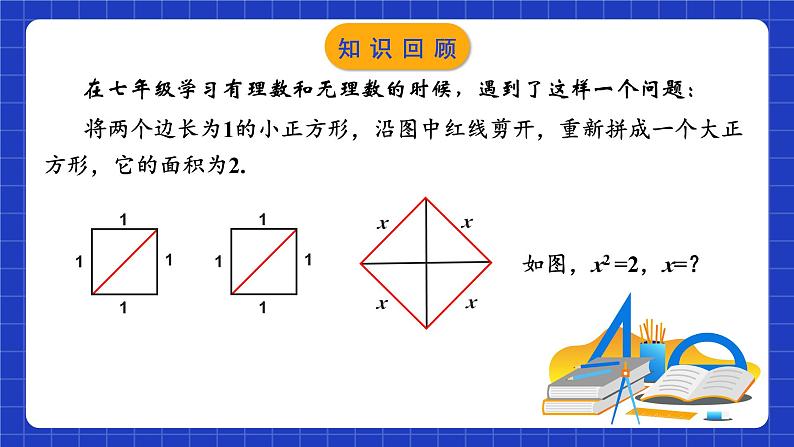
将两个边长为1的小正方形，沿图中红线剪开，重新拼成一个大正方形，它的面积为2.
在七年级学习有理数和无理数的时候，遇到了这样一个问题：
如图，x2 =2，x=？
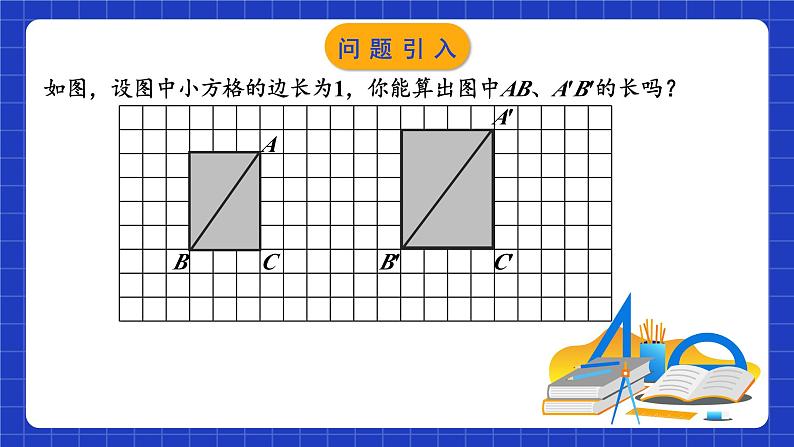
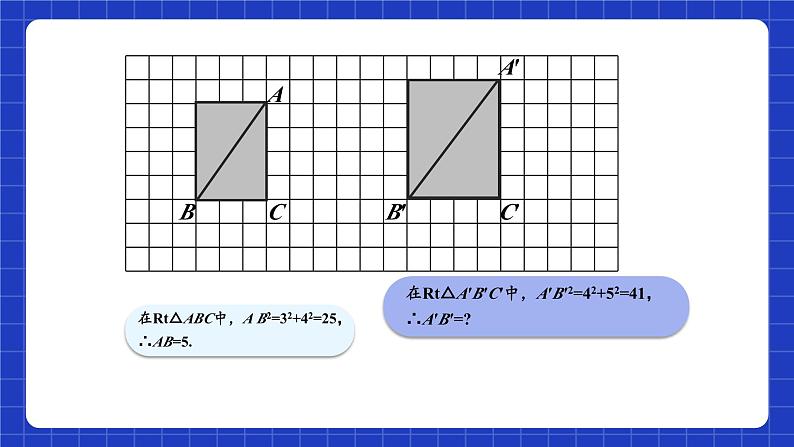
如图，设图中小方格的边长为1，你能算出图中AB、A′B′的长吗？
在Rt△ABC中，A B2=32+42=25，∴AB=5.
在Rt△A′B′C′中，A′B′2=42+52=41，∴A′B′=?
就是研究当x2=a时，x是什么数？
∵ 22=4， (-2)2=4，
∵(±2)2= 4，
∵ 0.52=0.25，(-0.5)2=0.25，
问题1：观察上面各式，等号右边的数都什么数？
∵ (±0.5)2=0.25，
问题2：使x2＝a(a>0)成立的数x有几个？它们之间有什么关系？
有两个，它们互为相反数.
问题3：当a=0时， x2 =a成立吗？如果成立，x=？
问题4：当a<0时， x2 =a成立吗？
如果x2＝a (a≥0)，那么x叫做a的平方根，也称为二次方根．
____是0.25的平方根
(-0.5)2=0.25
_____是0.25的平方根
(±0.5)2=0.25
0.25的平方根是±0.5
2的正的平方根是______，读作__________；
2的负的平方根是______，读作__________；
2的平方根是______，读作_______________.
读作 ____________；
正数a的正的平方根记作______，
正数a的负的平方根记作______，
正数a的两个平方根记作______，
读作 ______________.
A′B′2=42+52=41，A′B′=?
例1 求下列各数的平方根：
①正数有两个平方根，±不能丢；②求平方根时，结果能化简的 一般要化成最简结果；③带分数要先化为假分数； 再求平方根.
定义：求一个数的平方根的运算叫做开平方.
开平方与平方互为逆运算，所以可以通过平方运算来求一个数的平方根.
检验x是不是a的平方根，只要看x2是不是等于a即可.
与加、减、乘、除、乘方一样，是一种运算.
只有非负数才能进行开平方运算.
平方根是数，是开平方的结果.
一个数的一个平方根是7，那么它的另一个平方根是________，这个数是__________.
下列各数有平方根吗？如果有，请写出来；如果没有，请说明理由.
判断一个数有无平方根， 就看这个数是否为非负数.
一个正数有两个平方根，它们互为相反数；
1.下列各数有平方根吗？如果有，求出它的平方根.
2.判断下列说法是否正确：① -5是25的平方根（ ） ②25的平方根是-5 （ ）③0的平方根是0 （ ） ④只有正数有平方根（ ） ⑤ (-3)2的平方根是-3（ ）⑥3平方的平方根是3（ ）⑦-a没有平方根 （ ） ⑧把一个数先平方再开平方得原数（ ）
3.求下列各式中x的值：
(1)x2=16； (2)5x2－4＝11； (3)(x－1)2＝9.
由题可知x－1＝±3，∴x＝4或x＝－2.
一个正数的两个平方根为2x-1与5x-13，求x的值和这个数.
解：根据题意得：(2x-1)+(5x-13)=0 2x-1+5x-13 =0 2x+5x =1+13 7x =14 x =2
∵ 当x=2时，2x-1=2×2-1=4-1=3，∴ 32=9
或者 ∵ 当x=-2时， 5x-13=5×2-13=10-13=-3，∴ (-3)2=9
答：x的值为2，这个数为9.
2. (－0.6)2的平方根是(　　)A. －0.6 B. 0.6 C. ±0.6 D. 0.36
4.如果－b是a的平方根，那么(　　)A. b＝a2 B. a＝b2 C. b＝－a2　D. a＝－b2
5.下列有关平方根的叙述，正确的个数是(　　)①如果a存在平方根，那么a＞0；②如果a有两个不相等的平方根，那么a＞0；③如果a没有平方根，那么a＜0；④如果a＞0，那么a的平方根也大于0.A.1 B.2 C.3 D.4
6.若一个数的平方等于2，则这个数等于________.
7.若3x＋2有平方根，则x的取值范围为_________.
8.一个正数的两个不同的平方根分别是a－1和5－2a，则这个正数是_____.
10.写出下列各数的平方根：
(1) 4x2=81； (2)5x2-10=0； (3) (x-1)2=36.
11.求下列各式中x的值：