苏科版2024-2025学年八年级数学上册1.15构造三角形全等方法——截长补短和倍长中线(知识梳理与考点分类讲解)(学生版+解析)

这是一份苏科版2024-2025学年八年级数学上册1.15构造三角形全等方法——截长补短和倍长中线(知识梳理与考点分类讲解)(学生版+解析)，共21页。

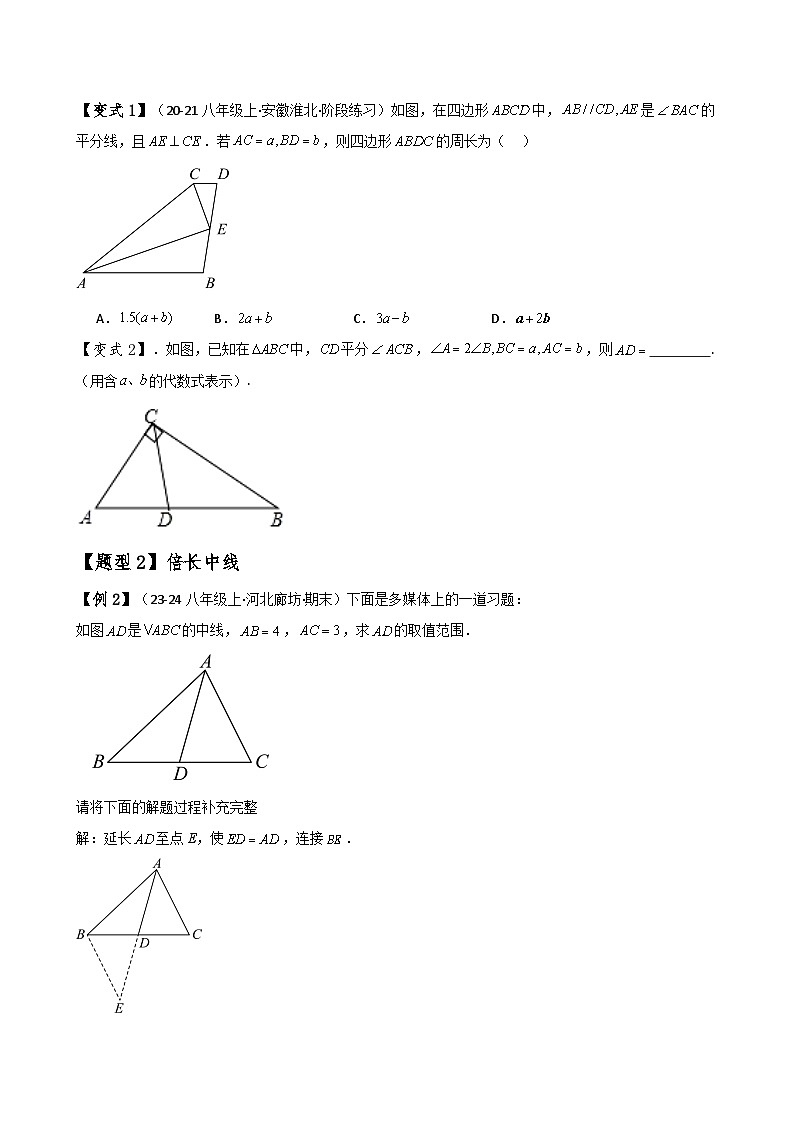
专题1.15 构造三角形全等方法——截长补短和倍长中线（知识梳理与考点分类讲解）第一部分【知识点归纳】当不能直接证明两个三角形全等时，可以通过添加适当的辅助线，使它们在两个合适的三角形之中，再证这两个三角形全等，本专题介绍截长补短法和倍长中线法.【知识点一】截长补短法截长法：在长边上截取一条与某一短边相同的线段，再证明剩下的线段与另一短边相等。补短法：延长较短线段至与另一条已知的较短线段的长度相等，然后证明新线段与最长的已知线段的关系。【知识点二】倍长中线法倍长中线：是指加倍延长中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等。常用于构造全等三角形。中线倍长法多用于构造全等三角形和证明边之间的关系（通常用“SAS”证明）第二部分【题型展示与方法点拨】【题型1】截长补短【例1】（23-24八年级·江苏·假期作业）如图，在中，，的角平分线、相交于点O，求证：．  【变式1】（20-21八年级上·安徽淮北·阶段练习）如图，在四边形中，是的平分线，且．若，则四边形的周长为（    ）A． B． C． D．【变式2】．如图，已知在中，平分，，则 . （用含的代数式表示）. 【题型2】倍长中线【例2】（23-24八年级上·河北廊坊·期末）下面是多媒体上的一道习题：如图是的中线，，，求的取值范围．   请将下面的解题过程补充完整解：延长至点E，使，连接．  ∵是的中线，∴__________，在和中，∴（__________填判定定理用字母表示）∴_________，在中，根据“三角形三边关系可知：__________________又∵∴__________________【变式1】（2024·山东临沂·一模）如图，点是的边上的中线，，，则的取值范围为（    ）A． B．C． D．【变式2】（23-24八年级上·四川德阳·阶段练习）如图，在中，为边的中线，为上一点，连接并延长交于点，若，，，则的长为 ．.第三部分【中考链接与拓展延伸】1、直通中考【例】（2021·黑龙江大庆·中考真题）已知，如图1，若是中的内角平分线，通过证明可得，同理，若是中的外角平分线，通过探究也有类似的性质．请你根据上述信息，求解如下问题：如图2，在中，是的内角平分线，则的边上的中线长的取值范围是 2、拓展延伸【例1】（23-24八年级上·江苏南通·期中）课外兴趣小组活动时，老师提出了如下问题：如图1，中，若，求边上的中线的取值范围．小明在组内经过合作交流，得到了如下的解决方法：如图1所示，延长到点，使，连接．请根据小明的思路继续思考：（1）由已知和作图能证得，得到，在中求得的取值范围，从而求得的取值范围是______________．方法总结：上述方法我们称为“倍长中线法”．“倍长中线法”多用于构造全等三角形和证明边之间的关系；（2）如图2，是的中线，，试判断线段与的数量关系，并加以证明；（3）如图3，在中，是的三等分点．求证：．【例2】（23-24八年级上·江西南昌·期中）综合与实践问题提出如图1，在中，平分，交于点D，且，则，，之间存在怎样的数量关系？并说明理由．方法运用  （1）我们可以通过作辅助线，构造全等三角形来解题．如图2，延长至点E，使得，连接，……，请判断，，之间的数量关系并补充完整解题过程．（2）以上方法叫做“补短法”．我们还可以采用“截长法”，即通过在上截取线段构造全等三角形来解题．如图3，在线段上截取，使得①______，连接②______．请补全空格，并在图3中画出辅助线．延伸探究（3）小明发现“补短法”或“截长法”还可以帮助我们解决其他多边形中的问题．如图4，在五边形中，，，，若，求的度数．专题1.15 构造三角形全等方法——截长补短和倍长中线（知识梳理与考点分类讲解）第一部分【知识点归纳】当不能直接证明两个三角形全等时，可以通过添加适当的辅助线，使它们在两个合适的三角形之中，再证这两个三角形全等，本专题介绍截长补短法和倍长中线法.【知识点一】截长补短法截长法：在长边上截取一条与某一短边相同的线段，再证明剩下的线段与另一短边相等。补短法：延长较短线段至与另一条已知的较短线段的长度相等，然后证明新线段与最长的已知线段的关系。【知识点二】倍长中线法倍长中线：是指加倍延长中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等。常用于构造全等三角形。中线倍长法多用于构造全等三角形和证明边之间的关系（通常用“SAS”证明）第二部分【题型展示与方法点拨】【题型1】截长补短【例1】（23-24八年级·江苏·假期作业）如图，在中，，的角平分线、相交于点O，求证：．  【答案】证明见解析【分析】根据三角形内角和定理和角平分线的定义，得到，，在上截取，连接，分别证明，，得到，即可证明结论．证明：，，、分别平分、，，，，，，如图，在上截取，连接，  在和中，，，，，，，在和中，，，，，．【点拨】本题考查了全等三角形的判定和性质，三角形内角和定理，角平分线的定义，做辅助线构造全等三角形是解题关键．【变式1】（20-21八年级上·安徽淮北·阶段练习）如图，在四边形中，是的平分线，且．若，则四边形的周长为（    ）A． B． C． D．【答案】B【分析】在线段AC上作AF=AB，证明△AEF≌△AEB可得∠AFE=∠B，∠AEF=∠AEB，再证明△CEF≌△CED可得CD=CF，即可求得四边形的周长．解：在线段AC上作AF=AB， ∵AE是的平分线，∴∠CAE=∠BAE，又∵AE=AE，∴△AEF≌△AEB（SAS），∴∠AFE=∠B，∠AEF=∠AEB，∵AB∥CD，∴∠D+∠B=180°，∵∠AFE+∠CFE=180°，∴∠D=∠CFE，∵，∴∠AEF+∠CEF=90°，∠AEB+∠CED=90°，∴∠CEF=∠CED，在△CEF和△CED中∵,∴△CEF≌△CED（AAS）∴CE=CF，∴四边形的周长=AC+AB+BD+CD=AC+AF+CF+BD=2AC+BD=，故选：B．【点拨】本题考查全等三角形的性质和判断．能正确作出辅助线构造全等三角形是解题关键．【变式2】．如图，已知在中，平分，，则 . （用含的代数式表示）. 【答案】a-b【分析】在CB上截取CA′=CA，连接DA′，根据SAS证明△ADC≌△A′DC，根据△ADC≌△A′DC，得出DA′=DA，∠CA′D=∠A，再证明DA′=A′B即可解决问题.解：在CB上截取CA′=CA，连接DA′， ∵CD平分∠ACB，∴∠ACD=∠A′CD，在△ADC和△A′DC中， ，∴△ADC≌△A′DC（SAS），∴DA′=DA，∠CA′D=∠A，∵∠A=2∠B，∠CA′D=∠B+∠A′DB，∴∠A′DB=∠B，∴BA′=A′D=AD，∴BC=CA′+BA′=AC+AD∴AD=BC-AC=a-b，故答案为：a-b.【点拨】本题属于三角形综合题，主要考查了全等三角形的判定与性质，等腰三角形的判定等，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.【题型2】倍长中线【例2】（23-24八年级上·河北廊坊·期末）下面是多媒体上的一道习题：如图是的中线，，，求的取值范围．   请将下面的解题过程补充完整解：延长至点E，使，连接．  ∵是的中线，∴__________，在和中，∴（__________填判定定理用字母表示）∴_________，在中，根据“三角形三边关系可知：__________________又∵∴__________________【分析】主要考查了全等三角形的判定与性质，三角形三边关系等知识，延长至点E，使．证明，推出，再利用三角形的三边关系，可得结论；解：延长至点E，使，连接，   ∵是的中线，∴，在和中，∴，∴，在中，根据“三角形三边关系”可知：，又∵，∴．【变式1】（2024·山东临沂·一模）如图，点是的边上的中线，，，则的取值范围为（    ）A． B．C． D．【答案】A【分析】本题考查了全等三角形的判定和性质、三角形三边之间的关系，解题的关键是作辅助线，构造全等三角形．延长至，使，连接．由证明，得，再根据三角形的三边关系即可求解．解：延长至，使，连接． 则，∵是边上的中线，∴，在和中， ，∴，∴，在中，，即，，故选：A．【变式2】（23-24八年级上·四川德阳·阶段练习）如图，在中，为边的中线，为上一点，连接并延长交于点，若，，，则的长为 ．.【答案】【分析】本题考查了全等三角形的判定和性质，等腰三角形的性质．延长至，使，连接，根据证明，则，根据可得，由此可得，即可得出，然后利用线段的和差即可求出的长．正确的作出辅助线构造全等三角形是解题的关键．解：如图，延长至G，使，连接，在和中，，．，，，，，．，，．故答案为：第三部分【中考链接与拓展延伸】1、直通中考【例】（2021·黑龙江大庆·中考真题）已知，如图1，若是中的内角平分线，通过证明可得，同理，若是中的外角平分线，通过探究也有类似的性质．请你根据上述信息，求解如下问题：如图2，在中，是的内角平分线，则的边上的中线长的取值范围是 【答案】【分析】根据题意得到，设AB＝2k，AC＝3k，在△ABC中，由三边关系可求出k的范围，反向延长中线至，使得，连接，最后根据三角形三边关系解题．【详解】如图，反向延长中线至，使得，连接，是的内角平分线，可设AB＝2k，AC＝3k，在△ABC中，BC＝5，∴5k＞5，k＜5，∴1＜k＜5，由三角形三边关系可知，∴故答案为：．【点拨】本题考查角平分线的性质、中线的性质、全等三角形的判定与性质、三角形三边关系等知识，是重要考点，难度一般，掌握相关知识是解题关键．2、拓展延伸【例1】（23-24八年级上·江苏南通·期中）课外兴趣小组活动时，老师提出了如下问题：如图1，中，若，求边上的中线的取值范围．小明在组内经过合作交流，得到了如下的解决方法：如图1所示，延长到点，使，连接．请根据小明的思路继续思考：（1）由已知和作图能证得，得到，在中求得的取值范围，从而求得的取值范围是______________．方法总结：上述方法我们称为“倍长中线法”．“倍长中线法”多用于构造全等三角形和证明边之间的关系；（2）如图2，是的中线，，试判断线段与的数量关系，并加以证明；（3）如图3，在中，是的三等分点．求证：．【答案】(1)；(2)，证明见解析；(3)见解析【分析】本题考查了三角形三边关系，三角形全等的性质与判定，利用倍长中线辅助线方法是解题的关键．（1）延长到点，使，连接，根据题意证明，可知，在中，根据，即可；（2）延长到，使得，连接，由（1）的结论以及已知条件证明，进而可得，由，即可求得与的数量关系；（3），取中点，连接并延长至点，使得，连接和，通过“倍长中线”思想全等证明，进而得到然后结合三角形的三边关系建立不等式证明即可得出结论．【详解】（1）解：如图1所示，延长到点，使，连接．∵是的中线，∴，在和中，，∴，∴，在中，，∴，即，∴，故答案为：．（2），理由：如图2，延长到，使得，连接，由（1）知，，∴，∵，∴，∵，即，又∵，∴∴，又∵，∴，∴，∵，∴，∵，∴．（3）证明：如图所示，取中点，连接并延长至点，使得，连接和，∵为中点， 为三等分点，∴，∴，在和中，，∴,同理可得: ,∴，此时, 延长交于 点，∵，∴，∵，∴，∴，∵，∴．【例2】（23-24八年级上·江西南昌·期中）综合与实践问题提出如图1，在中，平分，交于点D，且，则，，之间存在怎样的数量关系？并说明理由．方法运用  （1）我们可以通过作辅助线，构造全等三角形来解题．如图2，延长至点E，使得，连接，……，请判断，，之间的数量关系并补充完整解题过程．（2）以上方法叫做“补短法”．我们还可以采用“截长法”，即通过在上截取线段构造全等三角形来解题．如图3，在线段上截取，使得①______，连接②______．请补全空格，并在图3中画出辅助线．延伸探究（3）小明发现“补短法”或“截长法”还可以帮助我们解决其他多边形中的问题．如图4，在五边形中，，，，若，求的度数．【答案】（1），见解析（2）①AC   ②DF，见解析（3）【分析】（1）利用证明，得出，从而证得，所以，即可得出结论；（2）根据语言描述作出图形即可；（3）延长至点G，使，连接，利用证明，得出，，从而可证得．即可利用证明，得出，即可由求解．【详解】（1）．理由：∵平分，∴．又∵，，∴，∴．∵，∴．又∵，∴，∴．∵，∴．（2）①AC   ②DF．辅助线如图1所示．  （3）如图2，延长至点G，使，连接，．  ∵，，∴．∵，，，∴，∴，．∵，∴．又∵，，∴，∴．又∵，∴．【点拨】本题考查全等三角形的判定与性质，通过作辅助线构造全等三角形是解题的关键．