浙教版八年级数学上册第5章素养综合检测卷课件

这是一份浙教版八年级数学上册第5章素养综合检测卷课件，共47页。

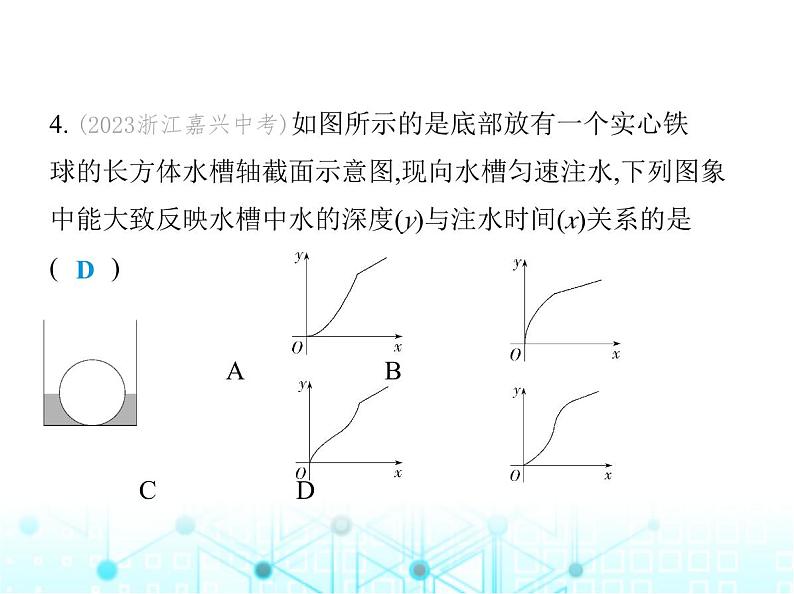
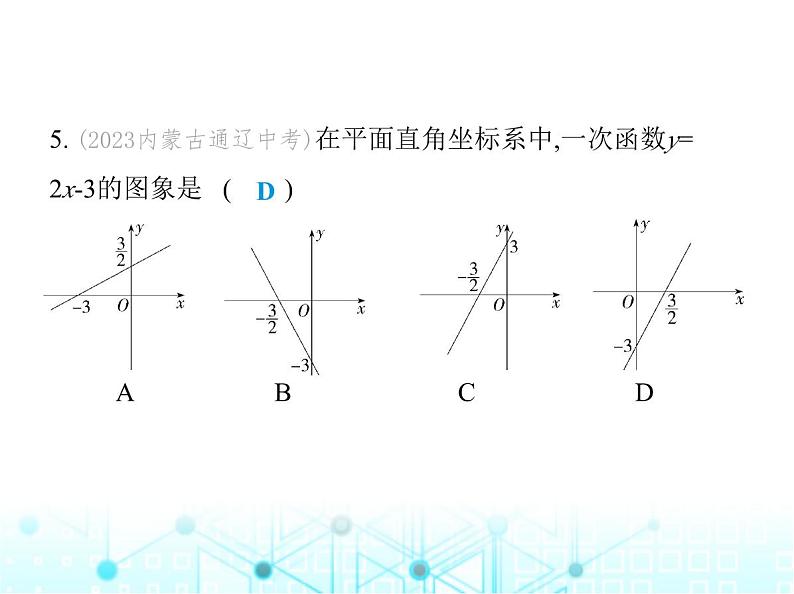
(满分100分, 限时60分钟)第5章　素养综合检测1. (跨学科·科学)(2024安徽合肥三十八中期中)腌制咸鸭蛋时,需要制作食盐水,一个容器中装有一定质量的水,向该容器中加入食盐,与食盐混合为食盐水,随着食盐的加入,食盐水的浓度(未达到饱和)将升高,这个问题中自变量和因变量分别是 (　　)A.水,食盐水的浓度　　    B.水,食盐水C.食盐量,食盐水　　     D.食盐量,食盐水的浓度一、选择题(每小题4分,共32分)D解析　随着食盐的加入,食盐水的浓度(未达到饱和)将升高,自变量是食盐量,因变量是食盐水的浓度.故选D.2. (2023江苏无锡中考)函数y= 中,自变量x的取值范围是 (　　)A.x>2　　    B.x≥2　　    C.x≠2　　    D.x<2C解析　由题意得x-2≠0,解得x≠2,故选C.3. (2023四川巴中中考)一次函数y=(k-3)x+2的函数值y随x的增大而减小,则k的取值范围是 (　　)A.k>0　　    B.k<0　　    C.k>3　　    D.k<3D解析　∵一次函数y=(k-3)x+2的函数值y随x的增大而减小,∴k-3<0,∴k<3,故选D.4. (2023浙江嘉兴中考)如图所示的是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是 (　　) 　     A　　     B　　      C　　     DD解析　水的深度先上升较慢,再变快,然后变慢,最后匀速上升.故选D.5. (2023内蒙古通辽中考)在平面直角坐标系中,一次函数y=2x-3的图象是 (　　)  A　　     B　　     C     DD解析　∵一次函数y=2x-3中的k=2>0,b=-3<0,∴一次函数y=2x-3的图象经过第一、三、四象限.故选D.6. (情境题·数学文化)(2023湖北武汉中考)皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积S=N+ L-1,其中N,L分别表示这个多边形内部与边界上的格点个数,在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知A(0,30),B(20,10),O(0,0),则△ABO内部的格点个数是 (　　)A.266　　    B.270　　    C.271　　    D.285C解析　由A(0,30)可知边OA上有31个格点(含点O,A),易知直线OB的解析式为y= x,∴当x为小于或等于20的正偶数时y也为整数,即OB边上有10个格点(不含端点O,含端点B);易知直线AB的解析式为y=-x+30,∴当0-2解析　将A(-2,0),B(0,-1)代入y=kx+b(k≠0),得 解得 ∴一次函数的解析式为y=- x-1.当y<0时,- x-1<0,∴x>-2,∴当函数值y<0时,x的取值范围为x>-2.故答案为x>-2.11. (情境题·革命文化)(2024陕西咸阳实验中学月考)为引导广大青少年树立正确的世界观、人生观、价值观,传承红色基因,赓续红色血脉,某校组织师生去红色革命圣地——延安开展研学旅行.已知汽车开始行驶时,油箱中有油50升,如果每小时耗油6升,则油箱余油量y(升)与行驶时间x(时)的关系式为　　 　    .y=-6x+50解析　根据题意,得y=50-6x=-6x+50,∴y与x的函数关系式为y=-6x+50.故答案为y=-6x+50.12. (2024陕西西咸新区期中)目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式:　　　    .y=5x解析　由题意得y=100×0.05x,即y=5x.故答案为y=5x.13. (情境题·科学研究)(2024广东深圳南山期末)如图①,2023年11月10日晚,“深爱万物”—2023深圳人才嘉年华活动正式启动,千余架无人机在深圳人才公园上空上演“天空之舞”,为人才喝彩、向人才致敬.如图②所示的平面直角坐标系中,线段OA,BC分别表示1号、2号无人机在队形变换中飞行高度y1(m),y2(m)与飞行时间x(s)的函数关系,其中y2=-4x+150,线段OA与BC交于点P,AB⊥y轴于点B,点A的横坐标为25,则在第　　　    秒时1号和2号无人机在同一高度.15解析　当x=0时,y2=150,∴点B的坐标为(0,150),由题意知,点A的坐标为(25,150),设y1=kx(k≠0),将(25,150)代入y1=kx,得150=25k,∴k=6,∴y1=6x,∴线段OA对应的函数表达式为y1=6x(0≤x≤25),令6x=-4x+150,解得x=15,∴6x=90,∴点P的坐标为(15,90),∴在第 15秒时1号和2号无人机在同一高度,为90 m.故答案为15.14. (跨学科·科学)图①所示的是一种指甲剪.该指甲剪利用了杠杆原理,使用者只需对按压柄的末端施力,便可轻易通过锋利的前端刀片剪断指甲,它被按压后的示意图如图②所示,上下臂OD=OF,∠CEO=90°,∠ABC=135°,杠杆BC=  mm,轴承CE=9 mm,未使用指甲剪时,点B,C在OD上,且EF比CD长1 mm,则OE的长为　　　    mm;使用指甲剪时,下压点A,当A′B′∥OF时,两刀片咬合,OD绕点O逆时针旋转到OD′的位置,则OD与CE的交点从开始到结束时移动的距离CG为　　　 mm.40解析　∵OD=OF,EF比CD长1 mm,∴OC=OE+1,∵∠CEO=90°,CE=9 mm,∴CE2+OE2=CO2,即92+OE2=(OE+1)2,∴OE=40 mm.已知∠CEO=90°,以E为坐标原点,EO所在直线为x轴,EC所在直线为y轴建立平面直角坐标系,延长A'B'交EC于点N,延长CB'交EO于点M,如图所示, 易知E(0,0),O(40,0),C(0,9),∵∠ABC=135°,∴∠A'B'C=135°,∴∠CB'N=∠ECM=45°,∵BC=  mm,∴CB'=  mm,∴CN=NB′=2 mm,∴NE=7 mm,∴B′(2,7),设直线OB'的解析式为y=kx+b(k≠0),将O(40,0),B'(2,7)代入得, ∴ ∴直线OB'的解析式为y=- x+ ,∴G ,∴EG=  mm,∴CG=9- = (mm).三、解答题(共44分)15. (2023北京中考)(8分)在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象经过点A(0,1)和B(1,2),与过点(0,4)且平行于x轴的直线交于点C.(1)求该函数的解析式及点C的坐标.(2)当x<3时,对于x的每一个值,函数y= x+n的值大于函数y=kx+b(k≠0)的值且小于4,直接写出n的值.解析　(1)把点A(0,1),B(1,2)代入y=kx+b(k≠0),得 解得 ∴该函数的解析式为y=x+1,由题意知,点C的纵坐标为4,当y=x+1=4时,x=3,∴C(3,4).(2)由(1)知,当x=3时,y=x+1=4,∵当x<3时,函数y= x+n的值大于函数y=x+1的值且小于4,∴当直线y= x+n过点(3,4)时满足题意,把(3,4)代入y= x+n,得4= ×3+n,解得n=2.16. (2023吉林长春中考)(10分)甲、乙两人相约登山,他们同时从入口处出发,甲步行登山到山顶,乙先步行15分钟到缆车站,再乘坐缆车直达山顶.甲、乙距山脚的垂直高度y(米)与甲登山的时间x(分钟)之间的函数图象如图所示:(1)当15≤x≤40时,求乙距山脚的垂直高度y与x之间的函数关系式.(2)求乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度.解析　(1)设乙距山脚的垂直高度y与甲的登山时间x之间的函数关系式为y=kx+b(k≠0),∵直线过(15,0)和(40,300),∴ 解得 ∴乙距山脚的垂直高度y与x之间的函数关系式为y=12x-180(15≤x≤40).(2)当25≤x≤60时,设甲距山脚的垂直高度y与甲的登山时间x之间的函数关系式为y=mx+n(m≠0),将(25,160)和(60,300)代入,得 解得 ∴y=4x+60(25≤x≤60).∵乙乘坐缆车上升过程中,和甲处于同一高度,∴ 解得 ∴乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度为180米.17. (2023辽宁阜新中考)(12分)某中学数学兴趣小组的同学们,对函数y=a|x-b|+c(a,b,c是常数,a≠0)的性质进行了初步探究,部分过程如下,请你将其补充完整.(1)当a=1,b=c=0时,即y=|x|.当x≥0时,函数化简为y=x;当x<0时,函数化简为y=　　　    .(2)当a=2,b=1,c=0时,即y=2|x-1|.①该函数自变量x和函数值y的若干组对应值如下表:-x其中m=　　　    .②在图①所示的平面直角坐标系内画出函数y=2|x-1|的图象.(3)当a=-2,b=1,c=2时,即y=-2|x-1|+2.4①当x≥1时,函数化简为y=　　　    .②在图②所示的平面直角坐标系内画出函数y=-2|x-1|+2的图象.(4)请写出函数y=a|x-b|+c(a,b,c是常数,a≠0)的一条性质:　    　     .(若所列性质多于一条,则仅以第一条为准)-2x+4当a>0时,函数y=a|x-b|+c有最低点(b,c)解析　(1)当x<0时,函数化简为y=-x.故答案为-x.(2)①当x=-1时,y=2×|x-1|=2×|-1-1|=4.故答案为4.②如图1所示. (3)①当x≥1时,函数化简为y=-2(x-1)+2=-2x+4,故答案为-2x+4.②如图2所示. (4)当a>0时,函数y=a|x-b|+c有最低点(b,c).答案合理即可.18. (2023江苏淮安淮阴中考)(14分)快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地卸装货物用时30 min,结束后,立即按原路以另一速度匀速返回,直至与慢车相遇,已知慢车的速度为70 km/h.两车之间的距离y(km)与慢车行驶的时间x(h)的函数图象如图所示.(1)请解释图中点A的实际意义.(2)求出图中线段AB的函数表达式.(3)两车相遇后,如果快车以返回的速度继续向甲地行驶,求到达甲地还需多长时间.解析　(1)A点的实际意义:出发3小时,快车到达乙地,此时快车与慢车相距120 km.(2)∵点B的横坐标为3+ =3.5(h),点B的纵坐标为120- ×70=85(km),∴点B的坐标为(3.5,85),设线段AB的函数表达式为y=kx+b(k≠0),将A(3,120),B(3.5,85)代入,得 解得 ∴线段AB的函数表达式为y=-70x+330(3≤x≤3.5).(3)快车从返回到遇见慢车所用的时间为4-3.5=0.5(h),∴快车从乙地返回甲地时的速度为85÷0.5-70=100(km/h),∵4×70÷100=2.8(h),∴两车相遇后,如果快车以返回的速度继续向甲地行驶,到达甲地还需2.8 h.