浙教版数学八上 第5章 一次函数 章节复习 课件

这是一份浙教版数学八上 第5章 一次函数 章节复习 课件，共37页。

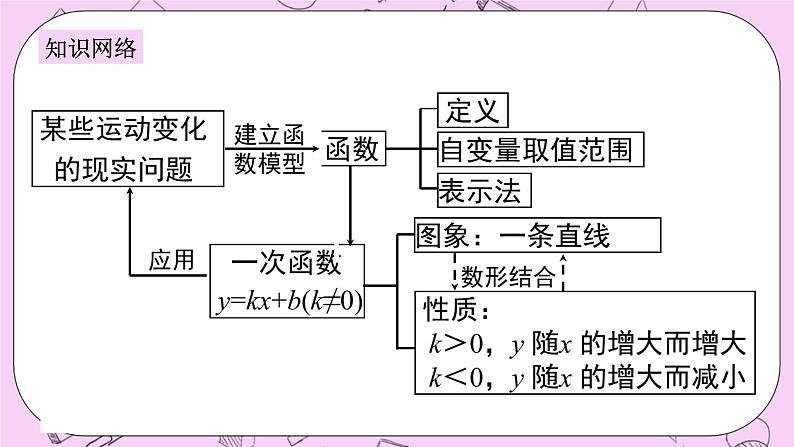
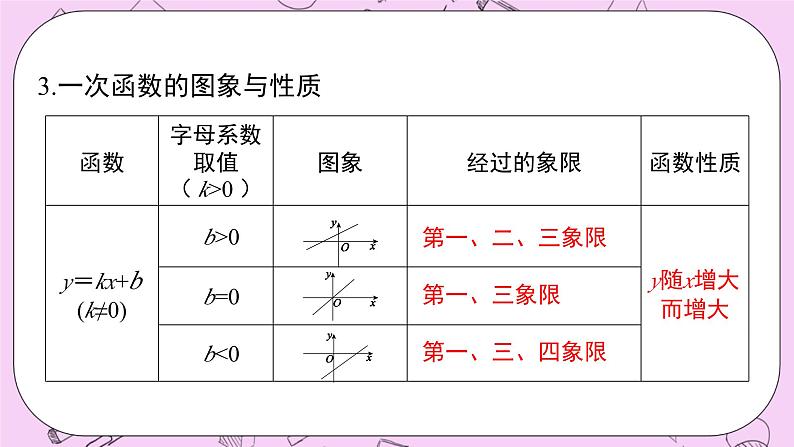
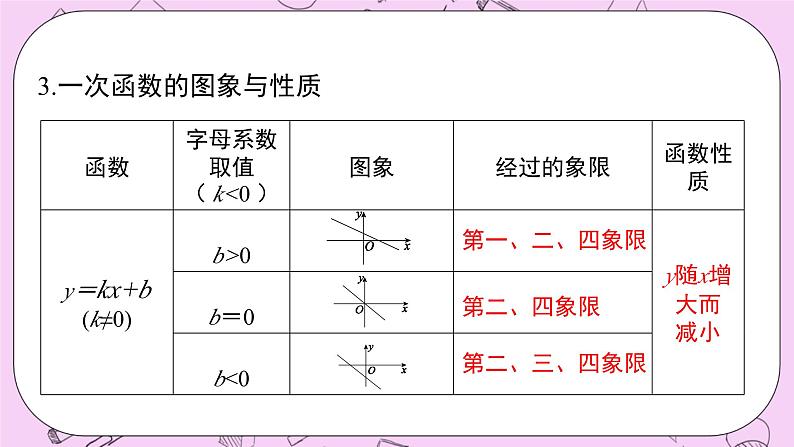
第5章 一次函数 章节复习浙教版八年级数学上册知识网络1. 常量与变量 叫变量， 叫常量.数值发生变化的量数值始终不变的量 在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数.一、函数2.函数定义：知识梳理 3.函数的图象： 对于一个函数，如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象.列表法解析式法图象法5.函数的三种表示方法：4.描点法画图象的步骤：列表、描点、连线0kx二、一次函数1.一次函数与正比例函数的概念2.分段函数 当自变量的取值范围不同时，函数的解析式也不同，这样的函数称为分段函数.第一、三象限 第一、二、三象限 第一、三、四象限 3.一次函数的图象与性质3.一次函数的图象与性质第一、二、四象限 第二、四象限 第二、三、四象限 求一次函数解析式的一般步骤：（1）先设出函数解析式；（2）根据条件列关于待定系数的方程（组）；（3）解方程（组）求出解析式中未知的系数；（4）把求出的系数代入设的解析式，从而具体写出这个解析式.这种求解析式的方法叫待定系数法.4.用待定系数法求一次函数的解析式考点一 函数的有关概念及图象【例1】 王大爷饭后出去散步，从家中走20分钟到离家900米的公园，与朋友聊天10分钟后，用15分钟返回家中．下面图形表示王大爷离家时间x（分）与离家距离y（米）之间的关系是（ ）ABCDD【点睛】利用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，理解问题的过程，能够通过图象得到函数问题的相应解决．考点解析1.下列变量间的关系不是函数关系的是（ ）A.长方形的宽一定，其长与面积B.正方形的周长与面积C.等腰三角形的底边长与面积D.圆的周长与半径C2.函数 中，自变量x的取值范围是（ ）A.x＞3 B.x＜3 C.x≤3 D.x≥-3B针对练习3.星期天下午，小强和小明相约在某公交车站一起乘车回学校，小强从家出发先步行到车站，等小明到了后两人一起乘公共汽车回到学校．图中折线表示小强离开家的路程y（千米）和所用的时间x（分）之间的函数关系．下列说法错误的是（ ）A．小强从家到公共汽车站步行了2千米B．小强在公共汽车站等小明用了10分钟C．公交车的平均速度是34千米/时D．小强乘公交车用了30分钟C考点二 正比例函数的图象与性质【例2】关于函数y=-5x，下列说法正确的是（　　）A.y随x的增大而增大 B.不论x为何值，总有y＞0C.必经过二、四象限 D.图象必经过点（0，5）C【点睛】本题考查了正比例函数的性质：它是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．考点二 正比例函数的图象与性质【例3】如图，三个正比例函数的图象对应的解析式为①y=ax，②y=bx，③y=cx，则a、b、c的大小关系是（　　）A.a＞b＞c B.c＞b＞a C.b＞a＞c D.b＞c＞aB【点睛】本题考查了正比例函数图象的性质，y=kx中，当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．同时注意直线越陡，则|k|越大．1.已知正比例函数y=kx（k≠0）的图象经过第二、四象限，则（　　）A.y随x的增大而减小B.y随x的增大而增大C.当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而减小D.无论x如何变化，y不变A D针对练习考点三 一次函数的图象与性质【例4】已知函数y=（2m+1）x+m﹣3；(1)若该函数是正比例函数，求m的值；(2)若函数的图象平行直线y=3x﹣3，求m的值；(3)若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围；(4)若这个函数图象过点（1，4），求这个函数的解析式.【分析】(1)由函数是正比例函数得m-3=0且2m+1≠0；(2)由两直线平行得2m+1=3；(3)一次函数中y随着x的增大而减小，即2m+1＜0；(4)代入该点坐标即可求解.考点解析解：(1)∵函数是正比例函数，∴m﹣3=0，且2m+1≠0， 解得m=3. (2)∵函数的图象平行于直线y=3x﹣3，∴2m+1=3， 解得m=1. (3)∵y随着x的增大而减小，∴2m+1＜0，解得m＜    ． (4)∵该函数图象过点（1,4），代入得2m+1+m-3=4, 解得m=2，∴该函数的解析式为y=5x-1.【点睛】一次函数的图象与y轴交点的纵坐标就是y=kx+b中b的值；两条直线平行，其函数解析式中的自变量系数k相等；当k＞0时，y随x的增大而增大；当k＜0时，y随x的增大而减小.考点三 一次函数的图象与性质【例5】已知一次函数y=（2m+1）x-m-1 的图象不经过第三象限，则m的取值范围是_________.【分析】不经过第三象限分两种情况：1.只经过二、四象限；2.经过一、二、四象限.所以需要进行分类讨论. m≤-11.一次函数y=-5x+2的图象不经过第______象限.2.点（-1，y1），（2，y2）是直线y=2x+1上两点，则y1____y2.三＜3.有下列函数：①　　　　 , ②　　　,③ , ④ . 其中函数图象过原点的是_____；函数y随x的增大而增大的是________；函数y随x的增大而减小的是_____；图象在第一、二、三象限的是______.②③①②③④4.已知一次函数y=-2x+3，当-2＜x≤3时，y的取值范围是________.-3≤x＜7针对练习5.点 P1 ( x1 ， y1 )， P2 ( x2 ， y2 )是一次函数y＝－2x－5图象上的两个点，且 x1 ＜ x2 ，则 y1 与 y2 的大小关系是___________ .y 1 ＞y 26.已知函数y=（m+1）x+（m2-1）当m取什么值时，y是x的一次函数？当m取什么值是，y是x的正比例函数．解：由函数是一次函数可得，m+1≠0，解得 m≠-1，所以，m≠-1时，y是x的一次函数；函数为正比例函数时，m+1≠0且m2-1=0，解得 m=1，所以，当m=1时，y是x的正比例函数．考点四 一次函数的“图象共存”问题【例6】直线y1=kx+b和y2=bx+k在同一平面直角坐标系内的大致图象为（　） A. B. C. D.A【点睛】一次函数的“图象共存”问题要把k、b决定经过象限的规律记牢；可以利用“假设法”来进行判定：先以其中一个函数的图象通过经过象限来确定k、b的符号；再通过k、b的符号判断另一个函数的图象经过哪些象限和实际经过的象限是否一致，如果一致，则“共存”；如果不一致，则“不共存”.考点解析直线y1=kx+b和y2=bx+k在同一平面直角坐标系内的大致图象为（ 　） A. B. C. D.B针对练习考点五 待定系数法求一次函数解析式【例7】一次函数的图象经过点A(-2，-3)，B(1,3)两点，求这个一次函数的表达式. 【点睛】利用待定系数法求一次函数的解析式；本题要注意利用一次函数的特点，来列出方程组，求出未知数的值从而求得其解析式；考点解析A(1，3) 、B(－2，0) 、C(－4，－2)三点是否在同一条直线上？为什么？ 针对练习考点五 待定系数法求一次函数解析式【例8】已知一次函数的图象经过点A（2，1），且与直线y=-2x-3平行，求这个一次函数的表达式． 【点睛】利用待定系数法求一次函数的解析式；本题要注意在同一坐标系中两直线平行，可以得到k值相等.考点解析【例9】已知一个一次函数的自变量的取值范围是2≤x≤6，函数值的取值范围是5≤y≤9，求这个一次函数解析式．考点五 待定系数法求一次函数解析式解：设该一次函数的关系式是：y=kx+b（k≠0）．一次函数y=kx+b的自变量的取值范围是：2≤x≤6，相应函数值的取值范围是：5≤y≤9，则  综上所述，该一次函数的解析式是y=x+3或y=-x+11．【点睛】本题考查了一次函数的性质、待定系数法求一次函数的解析式；解答该题时，采用了分类讨论的方法，以防漏解．【例10】已知一次函数的图象经过点（0，-2），且与两条坐标轴围成三角形的面积是4，试求一次函数的解析式．考点五 待定系数法求一次函数解析式 【点睛】利用待定系数法求一次函数解析式，坐标与图形性质，以及一次函数与坐标轴的交点，灵活运用待定系数法是解本题的关键．同时注意本题有两解，做题时不要漏解【例11】如图，直线l1与l2相交于点P，l1的函数表达式y=2x+3，点P的横坐标为-1，且l2交y轴于点A（0，-1）．求直线l2的函数表达式．考点五 待定系数法求一次函数解析式 【点睛】本题考查了利用待定系数法求一次函数的解析式：先设一次函数的解析式为y=kx+b（k≠0），然后把一次函数图象上的两点的坐标分别代入，得到关于k、b的方程组，解方程组求出k、b的值，从而确定一次函数的解析式．考点六 一次函数的平移规律（上、下平移）【例12】1.若将直线y=kx（k≠0）的图象向上平移3个单位长度后经过点（2，7），则平移后直线的解析式为（　　） A.y=2x+3 B.y=5x+3 C.y=5x-3 D.y=2x-3A【点睛】一次函数的上、下平移原则：上、下平移直线解析式k值不变，只改变b值，上加，下减.2.直线y＝-2x＋1向____平移_____个单位长度所得直线的解析式为y＝-2x－4.下5考点七 一次函数的实际应用(1)问符合题意的搭配方案有几种？请你帮助设计出来；(2)若搭配一个 A 种造型的成本是 800 元，搭配一个 B 种造型的成本是960元，试说明(1)中哪种方案成本最低？最低成本是多少元？【例14】为美化深圳市景，园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧，已知搭配一个 A 种造型需甲种花卉 80 盆，乙种花卉 40 盆，搭配一个 B 种造型需甲种花卉 50 盆，乙种花卉 90 盆．解：设搭配 A 种造型 x 个，则 B 种造型为(50－x)个，依题意，得 ∴31≤x≤33.∵x 是整数，x 可取 31,32,33，∴可设计三种搭配方案：①A 种园艺造型 31 个，B 种园艺造型 19 个；②A 种园艺造型 32 个，B 种园艺造型 18 个；③A 种园艺造型 33 个，B 种园艺造型 17 个． 解得方案①需成本：31×800＋19×960＝43040(元)；方案②需成本：32×800＋18×960＝42880(元)；方案③需成本：33×800＋17×960＝42720(元)．（2）方法一：方法二：成本为y＝800x＋960(50－x)＝－160x＋48000(31≤x≤33)．根据一次函数的性质，y 随 x 的增大而减小，故当 x＝33 时，y 取得最小值为33×800＋17×960＝42720(元)．即最低成本是 42720 元．【点睛】用一次函数解决实际问题，先理解清楚题意，把文字语言转化为数学语言，列出相应的不等式（方程），若是方案选择问题，则要求出自变量在取不同值时所对应的函数值，判断其大小关系，结合实际需求，选择最佳方案.1.李老师开车从甲地到相距240千米的乙地，如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系，其图象如图所示，那么到达乙地时油箱剩余油量是多少升？解：设一次函数的解析式为y＝kx＋35，将(160,25)代入，得160k＋35＝25，解得k＝ ，所以一次函数的解析式为y＝ x＋35.再将x＝240代入 y＝ x＋35，得y＝ ×240＋35＝20，即到达乙地时油箱剩余油量是20升．针对练习 2.小星以2米/秒的速度起跑后，先匀速跑5秒，然后突然把速度提高4米/秒，又匀速跑5秒.试写出这段时间里他的跑步路程s（单位：米）随跑步时间x（单位：秒）变化的函数关系式，并画出函数图象.解:依题意得s={2x(0≤x≤5) 10+6(x-5) (5