






还剩15页未读,
继续阅读
所属成套资源:人教版(2024)数学八年级上学期课件PPT全套
成套系列资料,整套一键下载
人教版八(上) 第15章 分式 章末复习 课件
展开
这是一份人教版八(上) 第15章 分式 章末复习 课件,共23页。
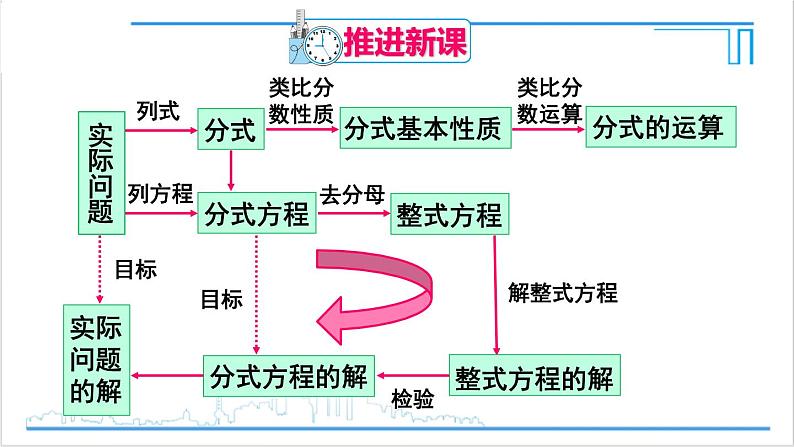
章末复习R·八年级上册新课导入导入课题 孔子说:“温故而知新.”学完《分式》这章后,希望同学们通过这一节课的复习,对《分式》这一章的知识有着更清晰更深刻的认识.学习目标(1)知道分式的意义,会运用分式的性质进行约分、通分.(2)熟练地进行分式的四则运算.(3)会解分式方程和列分式方程解决实际问题.推进新课分式分母中含有字母的式子叫分式.分式的基本性质分式的分母与分子乘(或除以)同一个不等于0的整式,分式的值不变.分式的运算加减法:乘除法:乘方法:分式的混合运算顺序:先乘方,后乘除,再加减.整数指数幂的运算性质:(1)am·an=am+n(m,n是整数)(2)(am)n=amn(m,n是整数)(3)(ab)n=anbn(n是整数)分母中含有未知数的方程叫做分式方程.分式方程的概念: 解分式方程先去分母,将分式方程转化为整式方程,方程两边同乘各分母的最简公分母,再解整式方程,最后检验.巩固练习 例1 计算:(1)(2)原式= = 6原式= =(3)原式= = = = (4)原式= = = = 例2 解下列分式方程:解:方程两边同乘以x2+x,得5x+2=3x解得 x = -1检验:当x=-1时, x2+x=0因此,x=-1不是原方程的解,方程无解.解:方程两边同乘以(2x+5)(2x-5),得2x(2x+5)-2(2x-5)=(2x+5)(2x-5)解得 x = 检验:当x= 时 , (2x+5)(2x-5)≠ 0因此,x= 是原方程的解. 随堂演练基础巩固1. 当x_____时,分式 无意义;当x_____时,分式 的值为0.=5= -12.把分式 中的a和b都扩大10倍,那么分式的值( )A.扩大为原来的2倍B.扩大为原来的4倍C.扩大为原来的10倍D.不变C3.一份工作,甲单独做a天完成,乙单独做b天完成,则甲乙两人合作一天的工作量是( )A. a+b B. C. D.D4.计算:(1)原式= = (2)原式= = = (3)原式= = = 综合应用5.已知 ,则分式 的值为多少?解:分子分母同除以xy,得6.A、B两地相距80公里,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍.已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.解:设公共汽车的速度为x公里/小时,则小汽车的速度为3x公里/小时,则根据题意,得解得:x=20.检验:当x=20时,3x≠0,所以x=20是原分式方程的解.答:公共汽车的速度为20公里/小时,小汽车的速度为60公里/小时.拓展延伸7.若关于x的方程 的解是正数,求实数a的取值范围.解:去分母,得2x+a=2-x,解得:因为x>0 且x≠2∴ >0 且 ∴a<2且a ≠ -4.课后作业1.从课后习题中选取;2.完成练习册本课时的习题。
章末复习R·八年级上册新课导入导入课题 孔子说:“温故而知新.”学完《分式》这章后,希望同学们通过这一节课的复习,对《分式》这一章的知识有着更清晰更深刻的认识.学习目标(1)知道分式的意义,会运用分式的性质进行约分、通分.(2)熟练地进行分式的四则运算.(3)会解分式方程和列分式方程解决实际问题.推进新课分式分母中含有字母的式子叫分式.分式的基本性质分式的分母与分子乘(或除以)同一个不等于0的整式,分式的值不变.分式的运算加减法:乘除法:乘方法:分式的混合运算顺序:先乘方,后乘除,再加减.整数指数幂的运算性质:(1)am·an=am+n(m,n是整数)(2)(am)n=amn(m,n是整数)(3)(ab)n=anbn(n是整数)分母中含有未知数的方程叫做分式方程.分式方程的概念: 解分式方程先去分母,将分式方程转化为整式方程,方程两边同乘各分母的最简公分母,再解整式方程,最后检验.巩固练习 例1 计算:(1)(2)原式= = 6原式= =(3)原式= = = = (4)原式= = = = 例2 解下列分式方程:解:方程两边同乘以x2+x,得5x+2=3x解得 x = -1检验:当x=-1时, x2+x=0因此,x=-1不是原方程的解,方程无解.解:方程两边同乘以(2x+5)(2x-5),得2x(2x+5)-2(2x-5)=(2x+5)(2x-5)解得 x = 检验:当x= 时 , (2x+5)(2x-5)≠ 0因此,x= 是原方程的解. 随堂演练基础巩固1. 当x_____时,分式 无意义;当x_____时,分式 的值为0.=5= -12.把分式 中的a和b都扩大10倍,那么分式的值( )A.扩大为原来的2倍B.扩大为原来的4倍C.扩大为原来的10倍D.不变C3.一份工作,甲单独做a天完成,乙单独做b天完成,则甲乙两人合作一天的工作量是( )A. a+b B. C. D.D4.计算:(1)原式= = (2)原式= = = (3)原式= = = 综合应用5.已知 ,则分式 的值为多少?解:分子分母同除以xy,得6.A、B两地相距80公里,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍.已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.解:设公共汽车的速度为x公里/小时,则小汽车的速度为3x公里/小时,则根据题意,得解得:x=20.检验:当x=20时,3x≠0,所以x=20是原分式方程的解.答:公共汽车的速度为20公里/小时,小汽车的速度为60公里/小时.拓展延伸7.若关于x的方程 的解是正数,求实数a的取值范围.解:去分母,得2x+a=2-x,解得:因为x>0 且x≠2∴ >0 且 ∴a<2且a ≠ -4.课后作业1.从课后习题中选取;2.完成练习册本课时的习题。
相关资料
更多









