人教B版 (2019)选择性必修 第一册2.5.1 椭圆的标准方程教课ppt课件

这是一份人教B版 (2019)选择性必修 第一册2.5.1 椭圆的标准方程教课ppt课件，共41页。PPT课件主要包含了练习A，练习B等内容，欢迎下载使用。

我们还知道，圆是平面内到圆心的距离等于半径的点的集合，圆上的点的特征是:任意一点到圆心的距离都等于半径，那么，你能说说到底什么是椭圆吗?圆上任意一点的特征是什么?
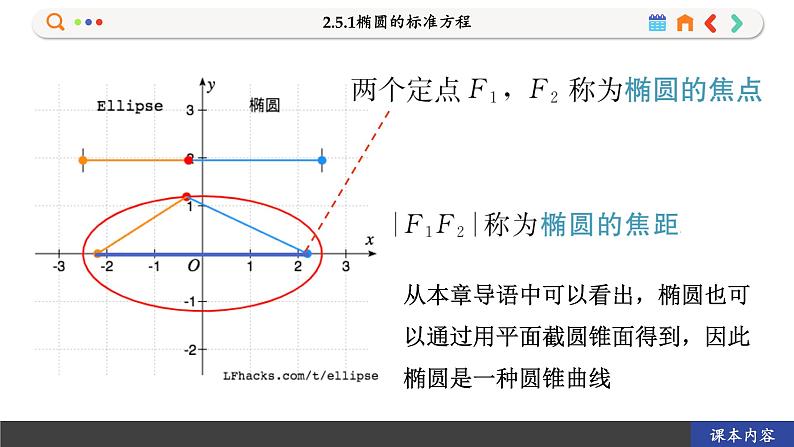
从本章导语中可以看出，椭圆也可以通过用平面截圆锥面得到，因此椭圆是一种圆锥曲线
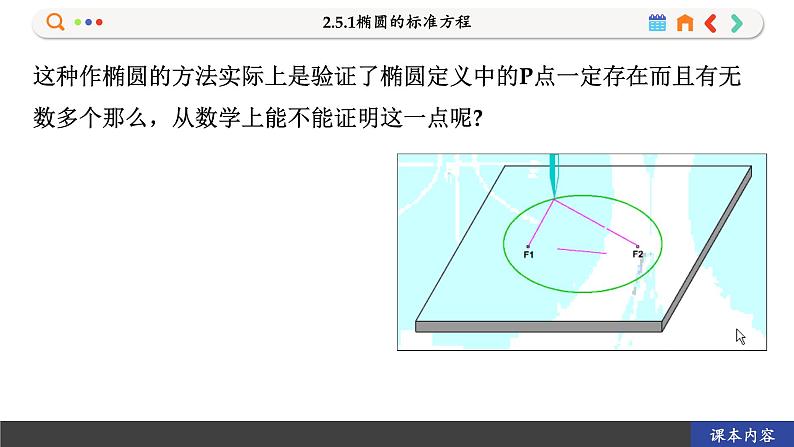
如图2-5-2所示，在平的画板上取两个定点F₁和F₂，在这两个点上都钉上一个图钉，将一条长度大于|F₁F₂|，的细绳的两端固定在两个图钉上，用笔尖把细绳拉紧，并使笔尖在画板上慢慢移动一周则画出的图形是一个椭圆.
这种作椭圆的方法实际上是验证了椭圆定义中的P点一定存在而且有无数多个那么，从数学上能不能证明这一点呢?
可以验证，方程⑨就是椭圆的方程，通常称为焦点在x轴上的椭圆的标准方程.
由上可以看出，椭圆的标准方程由a，c以及焦点的位置确定，其中a>c>0.
已知B，C是平面内的两个定点，|BC|=8，且平面内△ABC例 2的周长等于18，求这个三角形的顶点A的轨迹方程
取半径与圆柱底面半径相同的两个球，从平面a的两侧放入圆柱面内(这两个球都称为圆柱面的内切球)，并使得两个球都与平面a相切，切点分别为F₁，F₂。设P为交线C上任意一点，过P作圆柱的母线，分别与两个球相切于A，B.可以看出，PF₁与 PA 是同一个球的两条切线，PF₂ ，与PB也是同一个球的两条切线。
又因为 AB 的值是不变的，所以P到F₁与F₂的距离之和是一个常数，且|AB|>| F₁F₂ |，这就证明了C是一个椭圆!
有意思的是，利用类似的方法还能证明我们在本章导语中所提到的结论，即利用平面截圆锥面能得到椭圆、双曲线、抛物线，感兴趣的同学请查阅有关资料进一步了解吧!