初中数学苏科版八年级上册4.2 立方根说课课件ppt

这是一份初中数学苏科版八年级上册4.2 立方根说课课件ppt，共28页。PPT课件主要包含了学习目标，倍立方问题，体积边长3，x32x，立方根的定义，是8的立方根，的立方根是2，的立方根是3，三次根号，x3＝a等内容，欢迎下载使用。

1. 了解立方根的概念，会用根号表示数的立方根；
2. 了解开立方与立方是互逆的运算，会用立方运算求一些数的立方根；
3. 能运用立方根解决一些简单的实际问题.
传说中，公元前429年，一场瘟疫袭击了希腊第罗斯岛(Dels)，造成四分之一的人口死亡.岛民们推派一些代表去神庙请示阿波罗的旨意，神指示说：要想遏止瘟疫，得将阿波罗神殿中那正立方的祭坛加大一倍.人们便把每边增长一倍送到神那儿，于是神更加发火，他说，你们竟敢愚弄我！我要加倍惩罚你们！第罗斯岛人只好去求救于当时著名的学者柏拉图.
开始，柏拉图和他的学生认为这个问题很容易,试图用尺规作图作出它，均告失败，最后才发现这是一个尺规作图不能成功的问题.
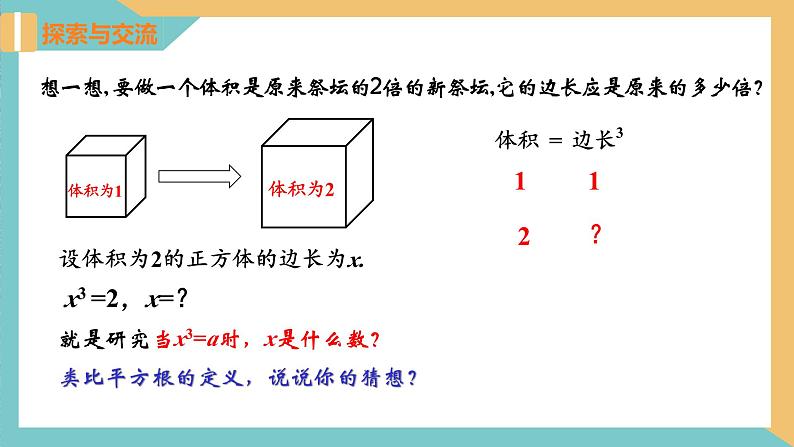
想一想, 要做一个体积是原来祭坛的2倍的新祭坛,它的边长应是原来的多少倍？
设体积为2的正方体的边长为x.
类比平方根的定义，说说你的猜想？
就是研究当x3=a时，x是什么数？
一般地，如果 x3＝a ，那么x叫做a的立方根，也称为三次方根．
____是27的立方根
立方根用什么符号表示呢？
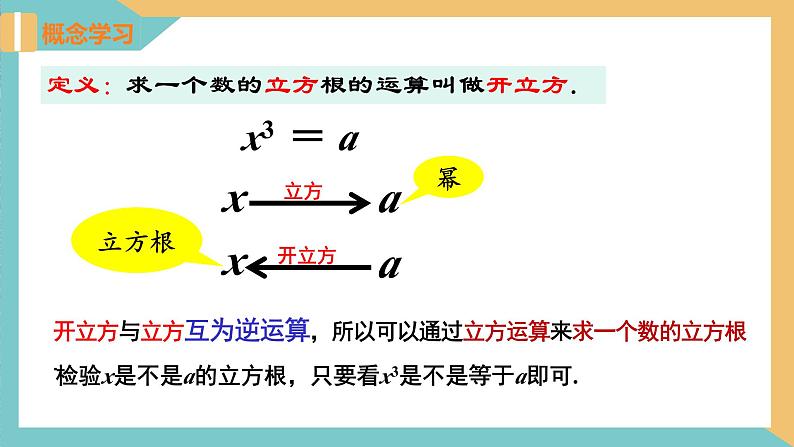
定义：求一个数的立方根的运算叫做开立方.
开立方与立方互为逆运算，所以可以通过立方运算来求一个数的立方根.
检验x是不是a的立方根，只要看x3是不是等于a即可.
例1 求下列各数的立方根：
1.写出下列各数的立方根：
(3)(x-1)3=125.
3.求下列各式中的x:
(1)8x3=27；
(2)-27x3=64；
(3) ∵ 53=125， ∴ x-1=5， ∴ x=6.
立方根与平方根的区别与联系：
如果x2＝a (a≥0)，那么x叫做a的平方根，也称为二次方根．
如果 x3＝a ，那么x叫做a的立方根，也称为三次方根．
一个正数有两个平方根，它们互为相反数.
一个正数有一个正的立方根；一个负数有一个负的立方根
被开方数的取值范围不同
被开方数是非负数，即 a≥0
开方运算与相应的乘方运算互为逆运算
都可以转化为非负数的非负方根来研究
0的平方根和立方根都是0
例2 把一个长12 cm，宽9 cm，高2 cm的长方体铁坯加工成一个正方体铁锭后，表面积有什么变化？(加工过程中无损失)
解：长方体的表面积为(12×9+9×2+12×2)×2=300(cm2).设正方体的棱长为x cm，则x3=12×9×2，解得x=6 .∴正方体的表面积为6×62=216(cm2) .300-216=84(cm2)，∴表面积减少了84 cm2.
解：由球的体积公式可知：
2. 已知a+1的算术平方根是3，﹣27的立方根是b-12，c-3的平方根是±2.求：(1)a，b，c的值；(2)a+4b﹣4c的立方根．
解：(1)∵a+1的算术平方根是3，∴a+1=9，a=8；∵-27的立方根是b-12，∴b-12=-3，b=9；∵c-3的平方根是±2，∴c-3=4，c=7；即a，b，c的值分别为8，9，7；
下列各数有立方根吗？如果有，请写出来；如果没有，请说明理由.
这几个式子有什么共同特征？
1. 求下列各式的值：
通过上述计算，你能发现什么规律？
通过以上计算，你发现了什么规律？
1.－27的立方根为( )A.±3 B.±9 C.－3 D.－9
3.下列说法正确的是(　　)A.如果一个数的立方根是这个数本身，那么这个数一定是0B.一个数的立方根不是正数就是负数C.负数没有立方根D.一个数的立方根与这个数同号，0的立方根是0
5. 平方根等于它本身的数有_____，立方根等于它本身的数有________；
6. 体积是125 dm3的正方体的棱长是________dm.
9.求下列各式中的x：
解：x3－64＝0，移项，得x3＝64，解得x＝4.
(2)(x＋1)3＝－8.
(1) x3－64＝0；
(x＋1)3＝－8，可得x＋1＝－2，解得x＝－3.
10. 某校在开展劳动教育剪纸课的时候，问同学们，你能用正方形纸片制作长方体纸盒吗？如图，在正方形的四个角剪下同样大小的四个小正方形，把剩下的纸片折叠成一个无盖的纸盒，然后把剪下的四个小正方形纸片拼起来作为纸盒的盖．如果我们希望做成的长方体的体积为32cm2，那么整张大正方形纸片的边长应是多少？
解：由题意，得(1-2x)+(3y-2)=0，
整理，得2x+1=3y，