初中数学人教版八年级下册19.2.2 一次函数图片ppt课件

这是一份初中数学人教版八年级下册19.2.2 一次函数图片ppt课件，共17页。PPT课件主要包含了学习目标，新课导入，复习回顾，典型例题，y-5x，y-5x+3，相同点，①都是一条直线，不同点，归纳总结等内容，欢迎下载使用。

1.会画一次函数的图象2.知道一次函数y=kx+b与正比例函数y=kx的图象间的关系3.理解一次函数的性质，并能利用一次函数性质解决问题
说一说正比例函数的图象和性质.
思考：正比例函数是特殊的一次函数，那么正比例函数的图象和性质与一次函数的有什么联系呢？
正比例函数y=kx（k≠0的常数）
k<0时，图象经过二、四象限，y随着x的增大而减小.
k>0时，图象经过一、三象限，y随着x的增大而增大；
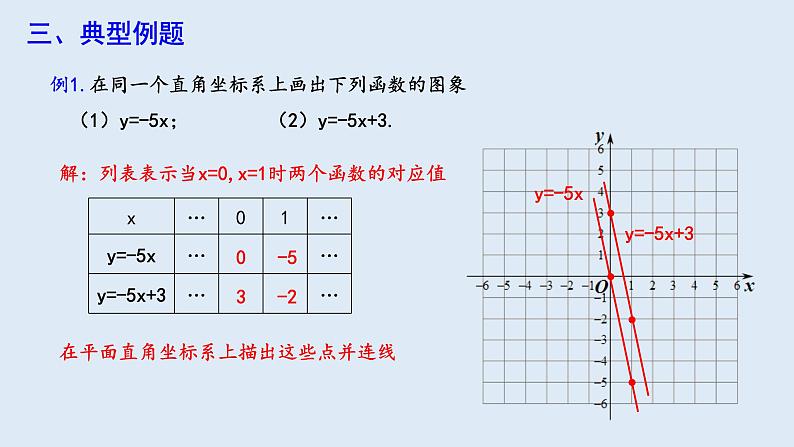
例1.在同一个直角坐标系上画出下列函数的图象 （1）y=-5x； （2）y=-5x+3.
解：列表表示当x=0,x=1时两个函数的对应值
在平面直角坐标系上描出这些点并连线
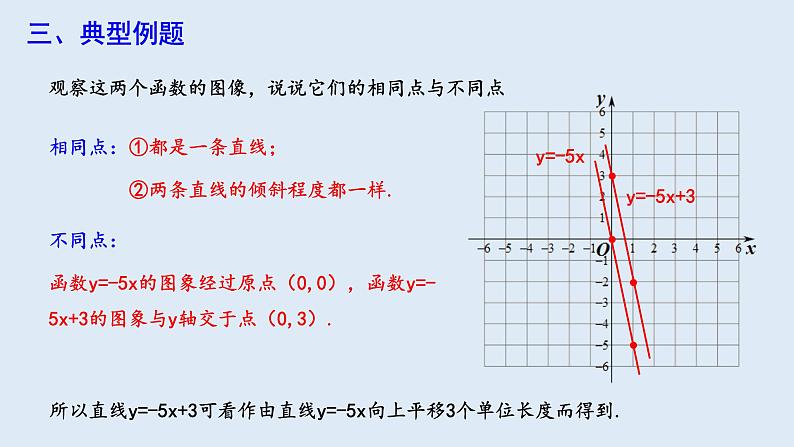
观察这两个函数的图像，说说它们的相同点与不同点
②两条直线的倾斜程度都一样.
函数y=-5x的图象经过原点（0,0），函数y=-5x+3的图象与y轴交于点（0,3）.
所以直线y=-5x+3可看作由直线y=-5x向上平移3个单位长度而得到.
一次函数y=kx+b(k≠0)的图象可以由直线y=kx平移|b|个单位长度得到（当b＞0时，向上平移；当b＜0时，向下平移）.一次函数y=kx+b(k≠0)的图象也是一条直线，我们称它为直线y=kx+b.
1.若把直线y=9x向下平移5个单位长度，再向上平移3个单位长度，则得到的图象解析式是（ ） A.y=9x+5 B.y=9x-5 C.y=9x-2 D.y=9x+8
解析：直线y=9x向下平移5个单位长度，得到：y=9x-5，
再向上平移3个单位长度，得到：y=9x-5+3=9x-2.
方法归纳：向上平移用加号，向下平移用减号.
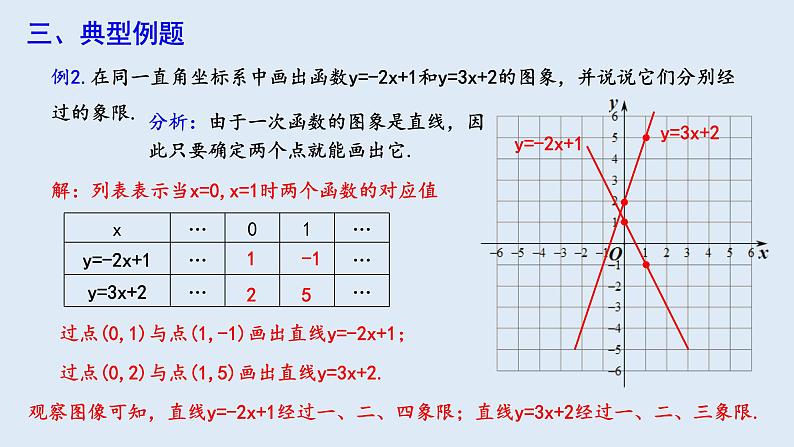
例2.在同一直角坐标系中画出函数y=-2x+1和y=3x+2的图象，并说说它们分别经过的象限.
分析：由于一次函数的图象是直线，因此只要确定两个点就能画出它.
过点(0,1)与点(1,-1)画出直线y=-2x+1；
过点(0,2)与点(1,5)画出直线y=3x+2.
观察图像可知，直线y=-2x+1经过一、二、四象限；直线y=3x+2经过一、二、三象限.
观察前面一次函数的图像，可以发现规律：
(1)当k＞0，b＞0时，直线经过第一、二、三象限；
当k＞0，b＜0时，直线经过第一、三、四象限；
当k＜0，b＞0时，直线经过第 一、二、四象限；
当k＜0，b＜0时，直线经过第二、三、四象限.
(2)当k＞0时，直线y=kx+b从左向右上升；
当k＜0时，直线y=kx+b从左向右下降.
当k＞0时，y随x的增大而增大； 当k＜0时，y随x的增大而减小.
性质：一次函数y=kx+b(k,b是常数，k≠0)中，
例3.已知一次函数y=(1-2m)x+m+1，求当m为何值时，（1）y随x的增大而增大?
分析：当k＞0时，y随x的增大而增大
解：∵y随x的增大而增大，
例3.已知一次函数y=(1-2m)x+m+1，求当m为何值时，（2）图象经过第一、二、四象限？
分析：当k＜0，b＞0时，图象经过第一、二、四象限
解：∵图象经过第一、二、四象限，
∴1-2m＜0，m+1＞0，
例3.已知一次函数y=(1-2m)x+m+1，求当m为何值时，（3）图象与y轴的交点在x轴的上方?
分析：当b＞0时，直线经过一、二、三象限或一、二、四象限，与y轴交点在x轴上方，同时一次函数还要满足k不能为0.
解：∵图象与y轴的交点在x轴的上方，
3.(1)一次函数y=2x+3的图象经过第 象限，y随x的增大而 ，与y轴交点坐标为 .(2)已知一次函数y=(m+2)x+1，函数y的值随x的值的增大而增大，则m的取值范围是 .
(1)一次函数y=kx+b(k≠0)的图象可以由直线y=kx平移|b|个单位长度得到（当b＞0时，向上平移；当b＜0时，向下平移）.一次函数y=kx+b(k≠0)的图象也是一条直线，我们称它为直线y=kx+b.
(2)当k＞0，b＞0时，直线经过第一、二、三象限；