人教版数学八年级下册 16.2.2 《二次根式的除法》课件+教学设计+导学案+分层练习（含答案解析）

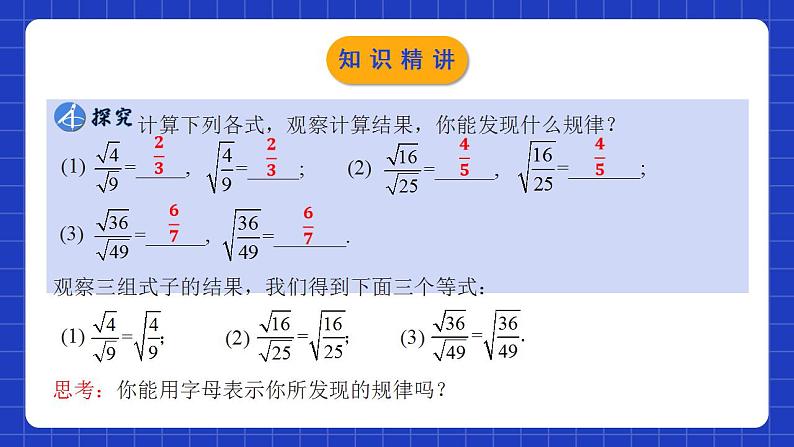
二次根式的除法学习目标0102031.了解二次根式的除法法则.（重点）2.会运用除法法则及商的算术平方根进行简单运算. （难点）3.能将二次根式化为最简二次根式.（重点）一、二次根式的乘法你都知道哪些核心知识？1.二次根式的乘法法则：语言表述：算术平方根的积等于各个被开方数积的算术平方根.即：二次根式相乘，________不变，________相乘.根指数被开方数应用范围：我们可以运用它来进行二次根式的解题和化简.语言表述：积的算术平方根，等于积中各因式的算术平方根的积.2.积的算术平方根的性质：复习回顾1.计算： 的结果是( ) A.2 B.6 C.8 D.16 二、练一练：B2.计算： 的结果是______. 3.等式 成立的条件是________.2x≥0复习回顾 (1) (2) (3) 观察三组式子的结果，我们得到下面三个等式：思考：你能用字母表示你所发现的规律吗？     知识精讲一般地，二次根式的除法法则是：语言表述：算术平方根的商等于被开方数商的算术平方根.即：二次根式相除，________不变，________相除.根指数被开方数当二次根式根号外的因数(式)不为1时，可类比单项式除以单项式法则，易得知识精讲例1.计算:解:典例解析计算：针对练习我们可以运用它来进行二次根式的解题和化简.语言表述：商的算术平方根，等于积中各因式的算术平方根的商.我们知道，把二次根式的乘法法则反过来就得到积的算术平方根的性质.类似的，把二次根式的除法法则反过来，就得到二次根式的商的算术平方根的性质:知识精讲例2.化简:解:补充解法：还有其他解法吗?典例解析化简:解:针对练习 前面我们学习了二次根式的除法法则，你会去掉 这样的式子分母的根号吗？把分母中的根号化去,使分母变成有理数的这个过程就叫做分母有理化.还有别的方法吗？知识精讲例3.计算:解:【点睛】分母形如 的式子，分子、分母同乘以 可使分母不含根号.典例解析（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式.我们把满足上述两个条件的二次根式，叫做最简二次根式.简记为：一根号无分母，分母无根号；二不能再开方.在二次根式的运算中，一般要把最后结果化为最简二次根式，并且分母中不含二次根式.观察上面三道例题中各小题的最后结果，可以发现这些式子中的二次根式有如下两个特点：知识精讲把下列二次根式化成最简二次根式：解:针对练习例4.设长方形的面积为S,相邻两边长分别为a,b.已知 ，求a的值.解:∵ ∴典例解析1.【章前引言】如果两个电视塔的高分别是h1km，h2km，那么它们的传播半径的比为 .这个式子还可以化简：这个比与地球半径无关. 这样，只要知道h1，h2，就可以求出比值.现在你会化简吗？针对练习 针对练习例5.计算：  典例解析 BAB达标检测 DC达标检测 达标检测8.已知等式 请你根据上述的规律，写出用正整数n(n>1)表示的式子___________________.达标检测9.把下列二次根式化成最简二次根式：解:达标检测10.化简.解:达标检测11.计算.达标检测  达标检测一般地，二次根式的除法法则是：语言表述：算术平方根的商等于被开方数商的算术平方根.即：二次根式相除，________不变，________相除.根指数被开方数当二次根式根号外的因数(式)不为1时，可类比单项式除以单项式法则，易得小结梳理课程结束