




- 【课时练】(湘教版) 2023-2024学年初中数学九年级上册 1.1 反比例函数 同步分层训练培优卷 试卷 0 次下载
- 【课时练】(湘教版) 2023-2024学年初中数学九年级上册 1.2 反比例函数的图像与性质 同步分层训练培优卷 试卷 0 次下载
- 【课时练】(湘教版) 2023-2024学年初中数学九年级上册 2.1 一元二次方程 同步分层训练培优卷 试卷 0 次下载
- 【课时练】(湘教版) 2023-2024学年初中数学九年级上册 2.2 一元二次方程的解法 同步分层训练培优卷 试卷 1 次下载
- 【课时练】(湘教版) 2023-2024学年初中数学九年级上册 2.4 一元二次方程根与系数的关系 同步分层训练培优卷 试卷 0 次下载
湘教版九年级上册1.3 反比例函数的应用精品课时训练
展开一、选择题
1.(2023·官渡)图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.图2是该台灯的电流I(A)与电阻R(Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象判断下列说法正确的是( )
A.I与R的函数关系式是I=200R(R>0)
B.当R<880时,I<0.25
C.当R>1000时,I>0.22
D.当880
A.2B.3C.4D.5
3.(2023·坪山模拟)密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化.已知密度ρ与体积V是反比例函数关系,它的图像如图所示,当V=5m3时,ρ=1.98kg/m3.根据图像可知,下列说法不正确的是( )
A.ρ与V的函数关系式是ρ=9.9V(V>0)
B.当ρ=9时,V=1.1
C.当V>5时,ρ>1.98
D.当3
A.I与R的关系式为I=R100B.I与R的关系式为I=20R
C.a
A.0
6.(2023·周口模拟)如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流I(A)与电阻R(Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是( )
A.当R<0.25时,I<880
B.I与R的函数关系式是I=200R(R>0)
C.当R>1000时,I>0.22
D.当880
A.用含I的代数式表示m为m=150−6I
B.电子体重秤可称的最大质量为120千克
C.当m=115时,若电源电压U为12(伏),则定值电阻R1最小为70(欧)
D.当m=115时,若定值电阻R1为40(欧),则电源电压U最大为10(伏)
8.(2022九上·崇仁月考)如图是反比例函数y=2x和y=ax(a>0,a为常数)在第一象限内的图象,点M在y=ax的图象上,MC⊥x轴于点C,交y=2x的图象于点A,MD⊥y轴于点D,交y=2x的图象于点B,当点M在y=ax的图象上运动时,以下结论:①△OBD与△OCA的面积相等;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中错误结论的个数是( )
A.0B.1C.2D.3
二、填空题
9.(2023·龙港模拟)如图,△ABO中,AO=2AB,点C为AO中点,BC的延长线交y轴于点E,BE∥x轴,过点A作AD⊥BE,垂足为点D,反比例函数y=kx(k>0)的图象经过点B,若阴影部分面积为4,则k的值为 .
10.(2023·鹿城模拟)为预防传染病,某校定期对教室进行“药熏消毒”.如图所示,药物燃烧阶段,教室内每立方米空气中的含药量y(mg)与燃烧时间x(分)成正比例;燃烧后,y与x成反比例.若y>1.6,则x的取值范围是 .
11.(2023·天门模拟)科技小组为了验证某电路的电压U(V)、电流I(A)电阻R(Ω)三者之间的关系:I=UR,测得数据如表格:那么,当电阻R=3.6Ω时,电流I= A.
12.(2023八下·宿城期末)如图,在平面直角坐标系中,一条直线与反比例函数y=8x(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=2x(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为 .
13.(2023·广元模拟)如图,在平面直角坐标系中,直线y=k1x+4与x轴交于点A,与y轴交于点C,与反比例函数y=k2x在第一象限内的图象交于点B,连接BO.若S△OBC=4,tan∠BOC=14,则k2的值是 .
三、解答题
14.(2022·钦州模拟)如图,一块砖的A,B,C三个面的面积比是4:2:1.如果B面向下放在地上,地面所受压强为aPa,那么A面和C面分别向下放在地上时,地面所受压强各是多少?
15.(2021八下·宝应期末)为了做好校园疫情防控工作,学校后勤每天对全校办公室和教室进行药物喷洒消毒,完成1间教室的药物喷洒要5min,药物喷洒时教室内空气中的药物浓度 y (单位: mg/m3 )与时间 x (单位:min)的函数关系式为 y=2x ,其图象为图中线段 OA ,药物喷洒完成后 y 与 x 成反比例函数关系,两个函数图象的交点为 A(m,n) ,当教室空气中的药物浓度不高于 1mg/m3 时,对人体健康无危害,如果后勤人员依次对一班至十一班教室(共11间)进行药物喷洒消毒当最后一间教室药物喷洒完成后,一班能否能让人进入教室?请通过计算说明.
四、综合题
16.(2023八下·泉州期末)如图1,在平面直角坐标系中,点A(−2,0),点B(0,2),直线AB与反比例函数y=kx(x>0)的图象在第一象限交于点C(a,4).
(1)求反比例函数的解析式
(2)如图2,点E(4,m)是反比例函数y=kx(x>0)图象上一点,连接CE,AE。试问在x轴上是否存在一点D,使△ACD的面积与△ACE的面积相等,若存在,请求出点D的坐标;若不存在,请说明理由。
(3)在(2)的条件下,坐标原点O关于点D的对称点为G,且点G在x轴的正半轴上,若点M是反比例函数的第一象限图象上一个动点,连接MG,以MG为边作正方形MGNF,当顶点F恰好落在直线AB上时,求点M的坐标。
17.(2023·三台模拟)如图,一次函数y=kx+b(k>0)的图象与反比例函数y=8x(x>0)的图象交于点A,与x轴交于点B,与y轴交于点C,AD⊥x轴于点D,CB=CD,点C关于直线AD的对称点为点E.
(1)点E是否在这个反比例函数的图象上?请说明理由;
(2)连接AE、DE,若四边形ACDE为正方形.点P在y轴上,当|PE−PB|最大时,求点P的坐标.
答案解析部分
1.【答案】D
【知识点】反比例函数系数k的几何意义;反比例函数的实际应用
【解析】【解答】解:A、∵k=880×0.25=220,
∴I与R的函数关系式是I=220R(R>0),A不符合题意;
B、当R<880时,I>0.25,B不符合题意;
C、当R=1000时,I=0.22,
当R>1000时,I<0.22,C不符合题意;
D、当880
【分析】根据反比例函数的图象与性质结合反比例函数k的几何意义对选项逐一判断即可求解。
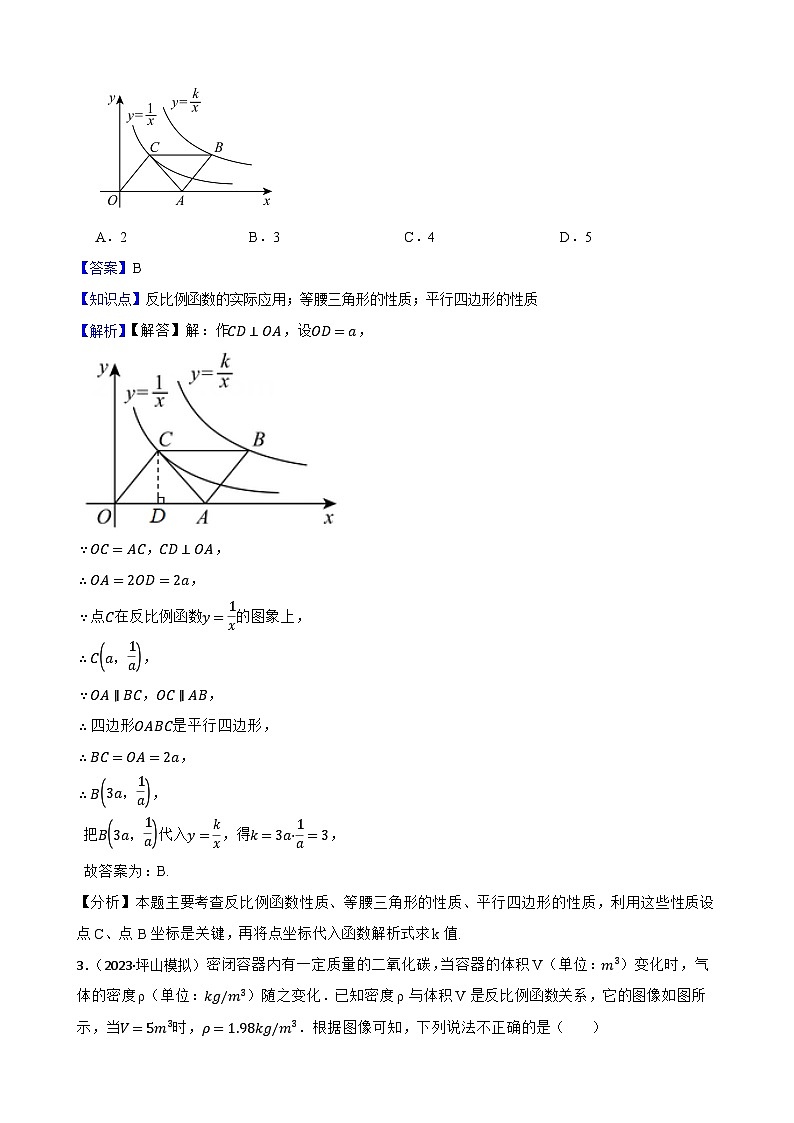
2.【答案】B
【知识点】反比例函数的实际应用;等腰三角形的性质;平行四边形的性质
【解析】【解答】解:作CD⊥OA,设OD=a,
∵OC=AC,CD⊥OA,
∴OA=2OD=2a,
∵点C在反比例函数y=1x的图象上,
∴Ca,1a,
∵OA∥BC,OC∥AB,
∴四边形OABC是平行四边形,
∴BC=OA=2a,
∴B3a,1a,
把B3a,1a代入y=kx,得k=3a·1a=3,
故答案为:B.
【分析】本题主要考查反比例函数性质、等腰三角形的性质、平行四边形的性质,利用这些性质设点C、点B坐标是关键,再将点坐标代入函数解析式求k值.
3.【答案】C
【知识点】反比例函数的实际应用
【解析】【解答】解:∵密度ρ与体积V是反比例函数关系,
∴可设ρ=mV.
∵图象过点(1.98,5),
∴m=1.98×5=9.9,
∴ρ=9.9V,故A正确;
令ρ=9,可得V=1.1,故B正确;
当V=3时,ρ=3.3;当V=9时,ρ=1.1,
∴当3
【分析】由题意可设ρ=mV,将(1.98,5)代入求出m的值,据此判断A;令ρ=9,求出V的值,据此判断B;分别令V=3、9,求出ρ的值,进而判断D.
4.【答案】D
【知识点】反比例函数的实际应用
【解析】【解答】解:∵闭合电路的电压为定值,
∴U=IR=5×20=100;
∴I与R的关系式为I=100R,故A、B错误;
由反比例函数的图象的性质可知,
∵k=100>0,
∴在第一象限,反比例函数I随R的增大而减小,
∵40<80,
∴a>b,故C错误.
当I=2时,R=1002=50,
由反比例函数的图象的性质可知,当2
【分析】根据“电流×电阻=电压”,由电压为定值可知电流和电阻成反比例关系,有表格可知当I=5,R=20,可求出I与R的关系式;再根据反比例函数的图象和性质即可解答.
5.【答案】B
【知识点】反比例函数的实际应用
【解析】【解答】解:设y=kx,将(0.5,200)代入可得k=0.5×200=100,
∴y=100x.
令y=400,可得x=0.25,
∴要配制一副度数小于400度的近视眼镜,焦距的取值范围为x>0.25.
故答案为:B.
【分析】设y=kx,将(0.5,200)代入求出k的值,得到反比例函数的解析式,令y=400,求出x的值,进而可得x的范围.
6.【答案】D
【知识点】反比例函数的实际应用
【解析】【解答】解:设I与R的函数关系式是I=UR(R>0),
∵该图象经过点P(880,0.25),
∴U880=0.25,
∴U=220,
∴I与R的函数关系式是I=220R(R>0),B不符合题意;
当R=0.25时,I=880,当R=1000时,I=0.22
∵反比例函数I=UR(R>0),I随R的增大而减小,
当R<0.25时,I>880,当R>1000时,I<0.22,故答案为:A,C不符合题意;
∵R=880时,I=0.25,当R=1000时,I=0.22,
∴当880
【分析】设I与R的函数关系式是I=UR,将P(880,0.25)代入求出U的值,得到对应的函数关系式,据此判断B;令R=0.25、R=1000,求出I的值,然后结合图象可判断A、C;根据R=880、1000对应的I的值结合图象可判断D.
7.【答案】C
【知识点】反比例函数的性质;列反比例函数关系式
【解析】【解答】解:A、由题意可得:I=UR1+R2=1260+-2m+240=12-2m+300,
解得:m=150-6I,
∴结论正确,不符合题意;
B、∵m=150-6I,
∴m随I的增大而增大,
∵0≤I≤0.2,
∴当I=0.2时,m的最大值为120,
∴结论正确,不符合题意;
C、当U=12,m=115时,R2=-2m+240=-2×115+240=10,
∵UR1+R2=U-2m+300,
∴1210+R1=12-2×115+300,
解得:R1=60,
∴结论C错误,符合题意;
D、当m=115时,R2=-2m+240=10,
∵R1=40,
∴U=(R1+R2)I=50I,
∵50>0,
∴U随I的增大而增大,
∵0≤I≤0.2,
∴当I=0.2时,U增大,最大值为10,
∴结论D正确,不符合题意;
故答案为:C.
【分析】结合题意,根据反比例函数计算求解即可。
8.【答案】A
【知识点】反比例函数图象上点的坐标特征;反比例函数-动态几何问题
【解析】【解答】∵点A、B在同一反比例函数y=2x的图像上,
∴S△OBD=S△OCA=|k|2=1.
故①符合题意;
∵点M在反比例函数y=ax的图象上,
∴S矩形OCMD=|a|=a.
∵S△OBD=S△OCA=1,
∴S四边形OAMB=a−2.
故②符合题意;
连接OM,可知S△OCM=S△ODM=a2.
∵点A是MC的中点,
∴S△AOC=S△AOM.
∵S△OBD=S△OCA,
∴S△BOD=S△BOM,
∴点B是MD的中点.
故③符合题意.
所以错误的个数是0.
故答案为:A.
【分析】利用反比例函数图象上的点坐标的特征和反比例函数k的几何意义逐项判断即可。
9.【答案】8
【知识点】反比例函数图象上点的坐标特征;反比例函数-动态几何问题
【解析】【解答】∵C是OA的中点,
∴OC=AC,
∵OA=2AB,
∴OC=AC=AB,
∵AD⊥BE,
∴CD=BD,
∴S△ACD=S△ABD,
在△OCE和△ACD中,
∠OCE=∠ACD∠OEC=∠ADC=90°OC=AC,
∴△OCE≌△ACD(AAS),
∴S△ACD=S△OCE,
∵阴影部分的面积为4,
∴S△OBC+S△OCE=S△OBC+S△ABD=S△BOE=4=12k,
∵k>0,
∴k=8,
故答案为:8.
【分析】先证出△OCE≌△ACD(AAS),可得S△ACD=S△OCE,再结合△OBC+S△OCE=S△OBC+S△ABD=S△BOE=4=12k,求出k的值即可。
10.【答案】2
【解析】【解答】解:函数图象可知,
燃烧时,y与x成正比例函数: y=k1x,
将(10,8)代入y=k1x得8=10k1,即k=45,
∴y=45x(0≤x<10),
燃烧后,y与x成反比例函数:y=kx,
将(10,8)代入y=kx得8=k10,即k=80,
∴y=80x(x≥10),
∵y>1.6,
∴1.6=45x即x=2;1.6=80x即x=50,
∴x的取值范围是2
11.【答案】10
【知识点】反比例函数的实际应用
【解析】【解答】解:把R=2,I=18,代入I=UR得:18=U2,
解得U=36,
∴I=36R,
当R=3.6Ω 代入I=363.6得:
I=363.6=10(Ω),
故答案为:10.
【分析】利用待定系数法求出I=36R,再将R=3.6Ω代入即可求出I值.
12.【答案】92
【知识点】梯形;反比例函数图象上点的坐标特征
【解析】【解答】解:∵点A、B在反比例函数y=8x(x>0)的图象上,
设点B的坐标为(8m,m),
∵点B为线段AC的中点,且点C在x轴上,
∴点A的坐标为(4m,2m).
∵AD∥x轴、BE∥x轴,且点D、E在反比例函数y=2x(x>0)的图象上,
∴点D的坐标为(1m,2m),点E的坐标为(2m,m).
∴S梯形ABED= 12(4m-1m+8m-2m)×(2m-m)=92
故答案为:92.
【分析】根据点A、B在反比例函数y=8x(x>0)的图象上,可设出点B坐标为(8m,m),再根据B为线段AC的中点可用m表示出来A点的坐标,由AD∥x轴、BE∥x轴,即可用m表示出来点D、E的坐标,结合梯形的面积公式即可得出结论.
13.【答案】16
【知识点】反比例函数的实际应用
【解析】【解答】∵直线y=k1x+4与x轴交于点A,与y轴交于点C,作BD⊥y轴交于点D
∴点C的坐标为(0,4),
∴OC=4,
∵S△OBC=4,
∴BD=2,
∵tan∠BOC=14,
∴BDAD=14
∴OD=8,
∴点B的坐标为(2,8),
∵反比例函数y=k2x在第一象限内的图象交于点B,
∴k2=2×8=16
【分析】首先根据直线求得点C的坐标,然后根据△BOC的面积求得BD的长,然后利用正切函数的定义求得OD的长,从而求得点B的坐标,求得结论.
14.【答案】解:设该砖的质量为m,则P•S=mg,
∵B面向下放在地上时地面所受压强为a帕,A,B,C三个面的面积之比是4:2:1,
∴把砖的A面向下放在地上,P=a÷42=0.5a ,把砖的C面向下放在地上P=a÷12=2a,
答:A面向下放在地上时,地面所受压强是0.5aPa,C面向下放在地上时,地面所受压强是2aPa.
【知识点】反比例函数的实际应用
【解析】【分析】设该砖的质量为m,则P•S=mg,由题意可得把砖的A面向下放在地上,P=a÷42,把砖的C面向下放在地上P=a÷12,计算即可.
15.【答案】解:∵完成1间教室药物喷洒需要5min,
∴完成11间教室药物喷洒需要55min,
∵当 x=5 时, y=2x=2×5=10 ,
∴A(5,10) ,
设反比例函数解析式为 y=kx ,
把 A(5,10) 代入解析式得: k=5×10=50 ,
∴反比例函数解析式为 y=50x ,
∴当 x=55 时, y=5055=1011<1 ,
∴一班学生能进入教室.
【知识点】反比例函数的实际应用
【解析】【分析】由题意可得完成11间教室药物喷洒需要55min,将x=5代入函数关系式中可得y的值,据此可得点A的坐标,设反比例函数解析式为 y=kx ,代入点A坐标可得k的值,据此可得反比例函数解析式,令x=55,求出y的值,与1进行比较即可.
16.【答案】(1)解:设直线AB的解析式为y=bx+n(b≠0)
将点A(−2,0),B(0,2)代入−2b+n=0n=2,解得b=1n=2
∴y=x+2
将点C(a,4)代入y=x+2, 得a+2=4,
解得a=2,
∴C(2,4),
将点C(2,4)代入y=kx 得k=8,
∴y=8x;
(2)解:把点E(4,m)代入y=8x得m=2,∴E(4,2)
设点E到AC的距离为h1,点D到AC的距离为h2
因为△ACD的面积与△ACE的面积相等,所以h1=h2,
∴DE∥AC
设直线DE的解析式为y=x+c,把点E(4,2)代入得,c=−2,
∴y=x−2,令y=0得x=2,
∴D(2,0)
当点D在x轴的负半轴时,D(−6,0),
∴D(2,0)或D(−6,0);
(3)解:过点M作QH∥x轴,过点F作FQ⊥QH于点Q,过点G作GH⊥QH于点H;
∴∠MQF=∠MHG=90,由题意可知:G(4,0)
在正方形MGNF中∠GMF=90,MG=MF
∴∠QMF=∠MGH,
∴△QMF≌△HGM(AAS)
∴QF=MH ,GH=QM
∵M在双曲线y=8x上,
∴设点M(t,8t),则点F(t−8t,8t−4+t)代入y=x+2
得 8t−4+t=t−8t+2,
解得t=83,
∴点M(83,3).
【知识点】两一次函数图象相交或平行问题;反比例函数与一次函数的交点问题;反比例函数-动态几何问题
【解析】【分析】(1)先用待定系数法,利用A、B两点的坐标求出直线AB的解析式,再利用AB直线的解析式求出点C的坐标,最后根据点C的坐标求出反比例系数k,即可求出反比例函数的解析式;
(2)先将点E(4,m)代入反比例函数y=8x中求出m,确定E的坐标,设点E到AC的距离为h1,点D到AC的距离为h2,若△ACD的面积与△ACE的面积相等,则h1=h2,根据平行线间的距离处处相等,可得DE∥AC,设直线DE的解析式为y=x+c,由点E的坐标即可求出直线DE的解析式,进一步可求出点D的坐标;
(3)过点M作QH∥x轴,过点F作FQ⊥QH于点Q,过点G作GH⊥QH于点H;在(2)的条件下,坐标原点O关于点D的对称点为G,且点G在x轴的正半轴上,可得G(4,0),先证△QMF≌△HGM,可得QF=MH,GH=QM,设点M(t,8t),则点F(t−8t,8t−4+t)代入y=x+2,即可求出t,从而求出点M的坐标.
17.【答案】(1)解:点E在这个反比例函数的图象上,
∵一次函数y=kx+b(k>0)的图象与反比例函数y=8x(x>0)的图象交于点A,
∴设点A的坐标为(m,8m),
∵点C关于直线AD的对称点为点E,
∴AD⊥CE,AD平分CE,
如图,连接CE交AD于H,
∴CH=EH,
∵BC=CD,OC⊥BD,
∴OB=OD,
∴OC=12AD,
∵AD⊥x轴于D,
∴CE∥x轴,
∴E(2m,4m),
∵2m×4m=8,
∴点E在这个反比例函数的图象上;
(2)解:∵四边形ACDE为正方形,
∴AD=CE,AD垂直平分CE,
∴CH=12AD,
设点A的坐标为(m,8m),
∴CH=m,AD=8m,
∴m=12×8m,
∴m=2或m=−2(负值舍去),
∴A(2,4),C(0,2),
延长ED交y轴于P,
∵CB=CD,OC⊥BD,
∴点B与点D关于y轴对称,
∴|PE−PD|=|PE−PB|,
则点P即为符合条件的点,
∵A(2,4),C(0,2),
∴D(2,0),E(4,2),
设直线DE的解析式为y=ax+n,
∴2a+n=04a+n=2,
∴a=1n=−2,
∴直线DE的解析式为y=x−2,
当x=0时,y=﹣2,
∴P(0,−2).
故当|PE−PB|最大时,点P的坐标为P(0,−2).
【知识点】反比例函数与一次函数的交点问题;反比例函数图象上点的坐标特征;反比例函数-动态几何问题
【解析】【分析】(1)设点A的坐标为(m,8m),连接CE交AD于H,先求出E(2m,4m),再结合2m×4m=8。即可得到点E在这个反比例函数的图象上;
(2)延长ED交y轴于P,设点A的坐标为(m,8m),先求出直线DE的解析式y=x−2,求出P(0,−2),即可得到答案。I(A)
5
⋯
a
⋯
⋯
⋯
b
⋯
⋯
R(Ω)
20
30
40
50
60
70
80
90
100
R(Ω)
2
4
6
9
I/(A)
18
9
6
4
湘教版九年级上册第4章 锐角三角函数4.2 正切优秀课后作业题: 这是一份湘教版九年级上册第4章 锐角三角函数4.2 正切优秀课后作业题,文件包含课时练湘教版2023-2024学年初中数学九年级上册42正切同步分层训练培优卷教师版docx、课时练湘教版2023-2024学年初中数学九年级上册42正切同步分层训练培优卷学生版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。
湘教版九年级上册3.6 位似优秀测试题: 这是一份湘教版九年级上册3.6 位似优秀测试题,文件包含课时练湘教版2023-2024学年初中数学九年级上册36位似同步分层训练培优卷教师版docx、课时练湘教版2023-2024学年初中数学九年级上册36位似同步分层训练培优卷学生版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
初中数学湘教版九年级上册3.3 相似图形精品练习题: 这是一份初中数学湘教版九年级上册3.3 相似图形精品练习题,文件包含课时练湘教版2023-2024学年初中数学九年级上册35相似图形的应用同步分层训练培优卷教师版docx、课时练湘教版2023-2024学年初中数学九年级上册35相似图形的应用同步分层训练培优卷学生版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。













