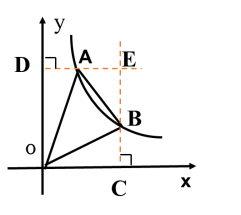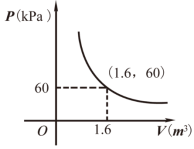湘教版九年级上册1.3 反比例函数的应用优秀教案设计
展开新湘教版 数学 九年级上 1.3 反比例函数的应用教学设计
课题 | 1.3 反比例函数的应用 | 单元 | 第一单元 | 学科 | 数学 | 年级 | 九年级 | |
学习 目标 |
| |||||||
重点 |
| |||||||
难点 | 反比例函数与其它知识点的综合题,体会建模思想。 | |||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 |
回顾知识 + 导入新课
回顾知识 + 导入新课
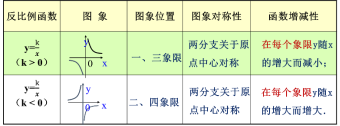
| 同学们,在上节课中我们已将学习了有关反比例函数的概念以及反比例函数的相关性质,今天我们将一起看反比例函数在生活中的具体应用和解决方法。接下来,我们一起回顾下前面学习的知识:
对于任意反比例函数y= ①长方形面积:S 平行四边形AOQB =|xy|= |k| ②三角形面积:S△QAO= S△QBO=
那么接下来,我们将一起看实际探究:
解 : 对于 (2) 若人对地面的压力 F=450N, 完成下表:
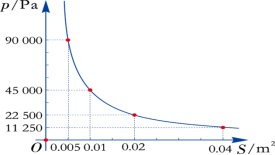
(3)当F=450N时,试画出该函数图象,并结合图象分析当受力面积S增大时,地面所受压强 P是如何变化的.据此请说出他们铺垫木板(木板重力忽略不计)通过湿地的道理.
解:当F=450N时,反比例函数的表达式: 由图象的性质可知,当受力面积S增大时,地面所受压强P会越来越小. 因此,该科技小组通过铺垫木板的方法来增大受力面积,以减小地面所受压强,从而可以顺利地通过湿地. 反比例函数在力学中的应用:应注意压强与受力面积的关系. 2.波义耳定律:在温度不变的情况下,气球内气体的压强p与它的体积V的乘积是一个常数k.即 PV=k(k为常数,k>0).你能运用这个定律解释:为什么使劲踩气球时,气球会爆炸吗? (1)在温度不变的情况下,气球内气体的压强p是它的体积V的反比例函数吗?写出它的解析式.
|
学生跟着教师回忆知识,并思考本节课的知识。
学生思考并回答问题。并跟着教师的讲解思路思考问题,并探究知识。
|
回顾学过的知识,帮学生复习知识,引出这节课的教学内容,同时也帮助学生能更好的融入课程。
导入新课,利用导入的例子引起学生的注意力。
|
讲授新课 + 例题讲解
讲授新课 + 例题讲解
讲授新课 + 例题讲解
讲授新课 + 例题讲解
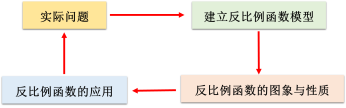
| 在反比例函数的实际应用中,我们要注意实际问题与反比例函数的建构与应用:
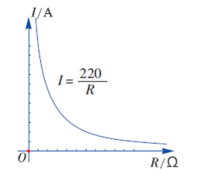
接下来,我们一起看几个例子: 【例1】已知某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间有如下关系式: U = IR, 且该电路的电压U恒为220 V. (1) 写出电流I 关于电阻R 的函数表达式; (2) 如果该电路的电阻为200 Ω, 则通过它的电流是多少? (3) 如图所示,如果该电路接入的是一个滑动变阻器, 怎样调整电阻R, 就可以使电路中的电流I增大? 分析:由于该电路的电压U 为定值, 即该电路的电阻R 与电流I 的乘积为定值, 因此该电路的电阻R与电流I成反比例关系. 解:(1)∵U = IR, 且U = 220 V, ∴IR = 220, 即电流I 关于电阻R函数表达式: (2)∵该电路的电阻R = 200 Ω,∴通过该电路的电流 (3)根据反比例函数
反比例函数在面积中的应用:应注意电压与、电流和电阻的关系.再运用反比例函数的性质求解. 在实际应用反比例函数的时候,在建立了函数模型时候,我们还要应用一定的方法,具体的如下:
反比例函数在生活中的具体应用
对于在力学、电学之中的应用我们之前的的例子已经讲解,现在我们一起看下其他的几种情况: 【例2】如图,已知,A,B是双曲线 (1)若A(2,3),求K的值. (2)在(1)的条件下,若点B的横坐标为3,连OA,OB,AB,求△OAB的面积.
解:(1)∵ A(2,3) ∴ (2)过A、B作y、X的垂线,垂足为D和C,两线交于E. ∵ A纵坐标=3,B横坐标=3 ∴E(3,3) ∴SOCED=3×3=9 又∵S△OAD=S△OCB= ∴S△OAB= SOCED-S△OAD-S△OCB=9-3-3=3. 反比例函数在面积中的应用:应注意三角形或者矩形的面积与k的关系. 【例3】近视眼镜的度数y(度)与焦距x(m)成反比例,已知200度近视眼镜镜片的焦距为0.5m. (1)试求眼镜度数y与镜片焦距x之间的函数关系式; (2)求800度近视眼镜镜片的焦距. 解:(1)设y= ∴所求的函数关系式为y= (2)当y=800时,800= ∴此时的焦距为0.125m. 反比例函数在光学中的应用:应注意找准关系,并建构合适的函数,再运用函数性质. 【例4】某工厂以每天30吨的速度生产一批货物,把把客户所要的货物全部生产恰好用了8天时间. (1)这批货物的总量是多少吨?在生产过程中,生产速度v(单位:吨/天)与生产时间t(单位:天)之间有怎样的函数关系? (2)若以每天40吨的速度生产货物,需要几天才能全部生产完? 解:∵ 生产总量=时间×工作效率 ∴总量=30×8=240(吨) ∵ 生产总量=卸货时间×工作效率 ∴ 解 答:需要6天才能全部生产完. 反比例函数在工程学中的应用:应注意“生产总量=时间×工作效率”,再运用函数性质. 反比例函数应用的注意点 1.弄清题目中的基本数量关系,将实际问题抽象成数学问题 . 2.分清自变量和函数,以便写出正确的函数关系式,并注意自变量的取值范围. 3.运用反比例函数的图象和性质,数形结合,分析和解决问题. |
结合导入的思考和老师的讲解,利用探究理解和掌握成反比例函数的应用。
老师在例题讲解的时候,自己先思考,然后再听老师讲解。
老师在例题讲解的时候,自己先思考,然后再听老师讲解。
老师在例题讲解的时候,自己先思考,然后再听老师讲解。
|
讲授知识,让学生知道本节课的学习内容和重点。
用例题讲解的方式将知识运用起来,便于学生的理解和记忆。
用例题讲解的方式将知识运用起来,便于学生的理解和记忆。
用例题讲解的方式将知识运用起来,便于学生的理解和记忆。 |
课堂练习
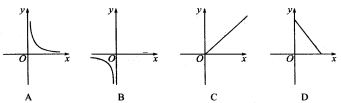
课堂练习 | 1.已知矩形的面积为24cm2,则它的长y与宽x之间的关系用图象大致可表示为(A )
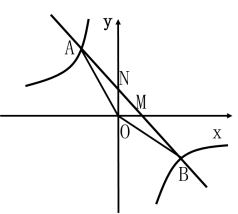
(2) 如果要求矩形的长不小于8cm,其宽≤3cm. 2.已知:如图,反比例函数
解:点A在反比例上,且纵坐标为3 ∴3=- 将A(-2,3)带入y=kx+1,即3=-2k+1,解得k=-1 ∴解析式为: y=-x+1 ∵反比例函数的面积不变性:S△ANO=S△BOM= ∴S△AOB= S△ANO+S△BOM 3.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸. 为了安全起见,气球的体积应( C ) A. 不大于 C. 不小于
由题意设P与V的函数关系式为 将(1.6,60)代入上式得k=96. 即 又∵P ≤ 120时,气球安全,∴ 4.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空. (1)蓄水池的容积是多少? (2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化? (3)写出t与Q之间的函数关系式; 解:(1)蓄水池的容积为:8×6=48(m3). (2)答:此时所需时间t(h)将减少. (3)t与Q之间的函数关系式为: |
学生自主完成巩固练习中的练习,然后在做完之后根据老师的讲解进一步巩固知识。
学生自主完成巩固练习中的练习,然后在做完之后根据老师的讲解进一步巩固知识。
|
借助练习,检测学生的知识掌握程度,同时便于学生巩固知识。
借助练习,检测学生的知识掌握程度,同时便于学生巩固知识。
|
课堂小结 | 在课堂的最后,我们一起来回忆总结我们这节课所学的知识点:
| 跟着老师回忆知识,并记忆本节课的知识。 | 帮助学生加强记忆知识。 |
板书 | 反比例函数的应用 | 借助板书,让学生知识本节课的重点。 | |
作业 | 教材第16页练习第2题. 教材第16页练习1.3第1题. 教材第17页练习1.2第2、4题. | ||
初中数学湘教版九年级上册1.1 反比例函数精品教学设计: 这是一份初中数学湘教版九年级上册1.1 反比例函数精品教学设计,共3页。教案主要包含了复习,情境导入,做一做,在面积中的应用,练一练,小结等内容,欢迎下载使用。
初中数学湘教版九年级上册第4章 锐角三角函数4.2 正切优质教学设计及反思: 这是一份初中数学湘教版九年级上册第4章 锐角三角函数4.2 正切优质教学设计及反思,共6页。
数学九年级上册1.3 反比例函数的应用获奖教学设计: 这是一份数学九年级上册1.3 反比例函数的应用获奖教学设计,共8页。