九年级上册1.3 反比例函数的应用优秀课后测评

1.3 反比例函数的应用

班级：___________姓名：___________得分：__________

（满分：100分，考试时间：40分钟）

一．选择题（共5小题，每题8分）

1．如果等腰三角形的面积为10，底边长为x，底边上的高为y，则y与x的函数关系式为（　　）

A．y=    B．y=    C．y=   D．y=

2．在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强，如下表：则可以反映y与x之间的关系的式子是（　　）

A．y=3 000x   B．y=6 000x   C．y=   D．y=

3．在一个可以改变容积的密闭容器内，装有一定质量m的某种气体，当改变容积V时，气体的密度p也随之改变，ρ与V在一定范围内满足ρ=，它的图象如图所示，则该气体的质量m为（　　）

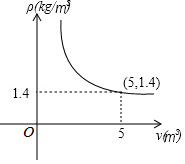
A．1.4kg   B．5kg   C．7kg   D．6.4kg

4．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m3）的反比例函数，其图象如图所示，当气球内的气压大于120kPa时，气球将爆炸，为了安全起见，气体体积应（　　）

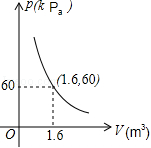
A．不小于m3   B．小于m3  C．不小于m3  D．小于m3

5．为了建设生态丽水，某工厂在一段时间内限产并投入资金进行治污改造，下列描述的是月利润y（万元）关于月份x之间的变化关系，治污改造完成前是反比例函数图象的一部分，治污改造完成后是一次函数图象的一部分，则下列说法不正确的是（　　）

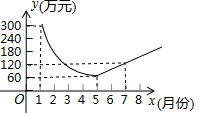
A．5月份该厂的月利润最低

B．治污改造完成后，每月利润比前一个月增加30万元

C．治污改造前后，共有6个月的月利润不超过120万元

D．治污改造完成后的第8个月，该厂月利润达到300万月

二．填空题（共4小题，每题5分）

6．已知圆柱的侧面积是10πcm2，若圆柱底面半径为rcm，高为hcm，则h与r的函数关系式是　   　．

7．京沪高速公路全长约为1262km，汽车沿京沪高速公路从上海驶往北京，汽车行驶完全程所需的时间t（h）与行驶的平均速度v（km/h）之间的函数关系式是t=　   　．

8．在照明系统模拟控制电路实验中，研究人员发现光敏电阻值R（单位：Ω）与光照度E（单位：lx）之间成反比例函数关系，部分数据如下表所示：

则光敏电阻值R与光照度E的函数表达式为　   　．

9．码头工人往一艘轮船上装载货物，装完货物所需时间y（min）与装载速度x（t/min）之间的函数关系如图（双曲线y=的一支）．如果以5t/min的速度卸货，那么卸完货物需要时间是　   　min．

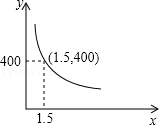
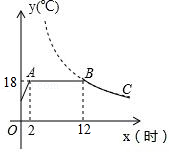
10．如图是某蔬菜大棚恒温系统从开启到关闭后，大棚内温度y（℃）随时间x（时）变化的函数图象，其中BC段是反比例函数图象的一部分，则当x=20时，大棚内的温度约为　   　℃．

三．解答题（共3小题，第10、12题各15分，第11题10分）

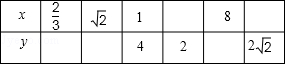
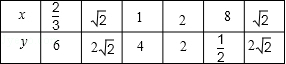
11．若矩形的长为x，宽为y，面积保持不变，下表给出了x与y的一些值求矩形面积．

（1）请你根据表格信息写出y与x之间的函数关系式；

（2）根据函数关系式完成上表．

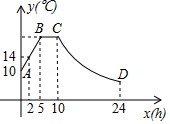
12．某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜．如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y （℃）与时间x（h）之间的函数关系，其中线段AB、BC表示恒温系统开启阶段，双曲线的一部分CD表示恒温系统关闭阶段．

请根据图中信息解答下列问题：

（1）求这天的温度y与时间x（0≤x≤24）的函数关系式；

（2）求恒温系统设定的恒定温度；

（3）若大棚内的温度低于10℃时，蔬菜会受到伤害．问这天内，恒温系统最多可以关闭多少小时，才能使蔬菜避免受到伤害？

13．阅读材料：以下是我们教科书中的一段内容，请仔细阅读，并解答有关问题．

公元前3世纪，古希腊学家阿基米德发现：若杠杆上的两物体与支点的距离与其重量成反比，则杠杆平衡，后来人们把它归纳为“杠杆原理”，通俗地说，杠杆原理为：

阻力×阻力臂=动力×动力臂

【问题解决】

若工人师傅欲用撬棍动一块大石头，已知阻力和阻力臂不变，分别为1500N和0.4m．

（1）动力F（N）与动力臂l（m）有怎样的函数关系？当动力臂为1.5m时，撬动石头需要多大的力？

（2）若想使动力F（N）不超过题（1）中所用力的一半，则动力臂至少要加长多少？

【数学思考】

（3）请用数学知识解释：我们使用撬棍，当阻力与阻力臂一定时，为什么动力臂越长越省力．

试题解析

一．选择题

1．C

【分析】利用三角形面积公式得出xy=10，进而得出答案．

【解答】解：∵等腰三角形的面积为10，底边长为x，底边上的高为y，

∴xy=10，

∴y与x的函数关系式为：y=．

故选：C．

【点评】此题主要考查了根据实际问题抽象出反比例函数解析式，根据已知得出xy=10是解题关键．

2．D

【分析】利用表格中数据得出函数关系，进而求出即可．

【解答】解：由表格数据可得：此函数是反比例函数，设解析式为：y=，

则xy=k=6000，

故y与x之间的关系的式子是y=，

故选：D．

【点评】此题主要考查了根据实际问题列反比例函数关系式，得出正确的函数关系是解题关键．

3．C

【分析】由图象知点（5，1.4）在函数的图象上，根据待定系数法就可求得函数解析式．求得m的值．

【解答】解：∵ρ=，

∴m=ρV，

而点（5，1.4）在图象上，

代入得m=5×1.4=7（kg）．

故选：C．

【点评】本题考查了反比例函数的应用，关键是要由点的坐标求出函数的解析式．

4．C

【分析】首先设P与V的函数解析式为P=，然后把点（1.6，60）代入可得P与V的函数解析式，把P=120代入可得V的值，进而可得答案．

【解答】解：设P与V的函数解析式为P=，

∵图象经过的点（1.6，60），

∴60=，

k=96，

∴P=，

当P=120时，V=，

∴为了安全起见，气体体积应不小于m3．

故选：C．

【点评】此题主要考查了反比例函数的应用，关键是正确理解题意，利用待定系数法求出反比例函数解析式．

5．C

【分析】直接利用已知点求出一次函数与反比例函数的解析式进而分别分析得出答案．

【解答】解：A、由函数图象可得，5月份该厂的月利润最低为60万，故此选选项正确，不合题意；

B、治污改造完成后，从5月到7月，利润从60万到120万，故每月利润比前一个月增加30万元，故此选选项正确，不合题意；

C、设反比例函数解析式为：y=，

则a=300，

故y=，

则120=，

解得：x=，

则只有3月，4月，5月，6月，7月共5个月的利润不超过120万元，故此选项错误，符合题意．

D、设一次函数解析式为：y=kx+b，

则，

解得：，

故一次函数解析式为：y=30x﹣90，

故y=300时，300=30x﹣90，

解得：x=13，

则治污改造完成后的第8个月，该厂月利润达到300万，故此选项正确，不合题意．

故选：C．

【点评】此题主要考查了一次函数与反比函数的应用，正确得出函数解析是解题关键．　

二．填空题

6．h=（r＞0）

【分析】圆柱的侧面积是一个长方形，根据面积=底面周长×高=2πrh可列出关系式．

【解答】解：由题意得：h与r的函数关系式是：h==，半径应大于0．

故本题答案为：h=（r＞0）．

【点评】根据题意，找到所求量的等量关系是解决问题的关键．

7．t=

【分析】根据等量关系“时间=路程÷速度”即可列出关系式．

【解答】解：由题意得：

汽车行驶完全程所需的时间t与行驶的平均速度v之间的函数关系式是t=．

故本题答案为：t=．

【点评】本题考查了反比例函数在实际生活中的应用，找出等量关系是解决此题的关键．

8．R=

【分析】直接利用表格中数据得出RE=30，进而得出答案．

【解答】解：由题意可得：RE=30，

则R=．

故答案为：R=．

【点评】此题主要考查了反比例函数的应用，正确得出RE=30是解题关键．

9．120

【分析】把（1.5，400）代入双曲线y=，可求y与x之间的函数关系式；利用函数关系式，当装载速度x=5时，得到y=，即可求解．

【解答】解：把（1.5，400）代入双曲线y=，得400=，解得k=600，

则y与x之间的函数关系式为y=；

当x=5时，y==120min．

故答案为：120．

【点评】此题主要考查了反比例函数的实际应用．解题的关键是根据实际意义列出函数关系式，从实际意义中找到对应的变量的值，利用待定系数法求出函数解析式，再根据题意进行解答．

10．10.8

【分析】利用待定系数法求反比例函数解析式即可；将x=20代入函数解析式求出y的值即可；

【点评】此题主要考查了反比例函数的应用以及待定系数法求一次函数解析式等知识，求出反比例函数解析式是解题关键．

三．解答题

11．【分析】（1）矩形的宽=矩形面积÷矩形的长，设出关系式，由于（1，4）满足，故可求得k的值；

（2）根据（1）中所求的式子作答．

【解答】解：（1）设y=，

由于（1，4）在此函数解析式上，那么k=1×4=4，

∴；

（2）4÷=4×=6，

=2，

4÷2=2，

=，

=．

【点评】解答该类问题的关键是确定两个变量之间的函数关系，然后利用待定系数法求出它们的关系式．在此函数上的点一定适合这个函数解析式．

12．【分析】（1）应用待定系数法分段求函数解析式；

（2）观察图象可得；

（3）代入临界值y=10即可．

【解答】解：（1）设线段AB解析式为y=k1x+b（k≠0）

∵线段AB过点（0，10），（2，14）

代入得

解得

∴AB解析式为：y=2x+10（0≤x＜5）

∵B在线段AB上当x=5时，y=20

∴B坐标为（5，20）

∴线段BC的解析式为：y=20（5≤x＜10）

设双曲线CD解析式为：y=（k2≠0）

∵C（10，20）

∴k2=200

∴双曲线CD解析式为：y=（10≤x≤24）

∴y关于x的函数解析式为：

y=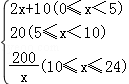

（2）由（1）恒温系统设定恒温为20°C

（3）把y=10代入y=中，解得，x=20

∴20﹣10=10

答：恒温系统最多关闭10小时，蔬菜才能避免受到伤害．

【点评】本题为实际应用背景的函数综合题，考查求得一次函数、反比例函数和常函数关系式．解答时应注意临界点的应用．

13．【分析】（1）根据杠杆定律求得函数的解析式后代入l=1.5求得力的大小即可；

（2）将求得的函数解析式变形后求得动力臂的大小，然后即可求得增加的长度；

（3）利用反比例函数的知识结合杠杆定律进行说明即可．

【解答】解：（1）根据“杠杆定律”有FL=1500×0.4，

∴函数的解析式为F=，

当L=1.5时，F==400，

因此，撬动石头需要400N的力；

（2）由（1）知FL=600，

∴函数解析式可以表示为：l=，

当F=400×=200时，l==3，

3﹣1.5=1.5（m），

因此若用力不超过400N的一半，则动力臂至少要加长1.5米；

（3）因为撬棍工作原理遵循“杠杆定律”，当阻力与阻力臂一定时，其乘积为常数，设其为k，则动力F与动力臂L的函数关系式为F=，根据反比例函数的性质可知，动力F随动力臂l的增大而减小，所以动力臂越长越省力．

【点评】本题考查了反比例函数的应用，解题的关键是从实际问题中抽象出反比例函数模型，体现了数学建模的数学思想，难度不大．