初中数学湘教版九年级上册第1章 反比例函数1.2 反比例函数的图像与性质精品巩固练习

这是一份初中数学湘教版九年级上册第1章 反比例函数1.2 反比例函数的图像与性质精品巩固练习，文件包含课时练湘教版2023-2024学年初中数学九年级上册12反比例函数的图像与性质同步分层训练培优卷教师版docx、课时练湘教版2023-2024学年初中数学九年级上册12反比例函数的图像与性质同步分层训练培优卷学生版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

1．（2023九上·临渭期末）已知反比例函数y＝kx（k≠0）与正比例函数y＝﹣2x没有交点，且双曲线图象上有三点A（﹣1，a）、B（﹣3，b）、C（4，c），则a、b、c的大小关系为（ ）
A．a＞b＞cB．b＞a＞cC．c＞b＞aD．c＞a＞b
【答案】C
【知识点】正比例函数的图象和性质；反比例函数的性质
【解析】【解答】解：∵正比例函数的解析式为y=−2x，
∴正比例函数图象经过二、四象限，
∵反比例函数y=kx与正比例函数y=−2x没有交点，
∴反比例函数图象不在二、四象限即反比例函数图象在一、三象限，
∴当x＜0时，y随x增大而减小，当x＞0时y随x增大而减小，且在第三象限内，反比例函数的函数值都小于0，第一象限内，反比例函数的函数值大于0，
∵-3<-1<0<4，
∴c＞b＞a.
故答案为：C.
【分析】根据正比例函数的解析式可得其图象经过二、四象限，由反比例函数与正比例函数没有交点可知反比例函数图象在一、三象限，且在每一象限内，y随x增大而减小，据此进行比较.
2．（2023九上·礼泉期末）已知反比例函数y=m−3x的图象位于第一、三象限，则m的取值范围是（ ）
A．m＞3B．m＞-3C．m＜3D．m＜-3
【答案】A
【知识点】反比例函数的性质
【解析】【解答】解：∵ 反比例函数y=m−3x的图象位于第一、三象限，
∴m-3＞0
解之：m＞3.
故答案为：A
【分析】利用反比例函数y=kx（k≠0），当k＞0时，图象分支在第一、三象限；当k＜0时，图象分支在第二、四象限，据此可得到关于m的不等式，然后求出不等式的解集.
3．（2023九上·新邵期末）对于反比例函数y=−2023x.下列说法不正确的是（ ）
A．图象分布在二，四象限内
B．图象经过点(1，−2023)
C．当x>0时，y随x的增大而增大
D．若点A(x1，y1)，B(x2，y2)都在函数的图象上，且x1【答案】D
【知识点】反比例函数的性质
【解析】【解答】解：∵y=−2023x，k=−2023<0，
∴图象过二，四象限，在每一个象限内，y随x的增大而增大，
当x=1时，y=−2023，
∴图象经过点(1，−2023)，
A、选项正确，不符合题意；
B、选项正确，不符合题意；
C、选项正确，不符合题意；
D、当x1<0y2，选项错误，符合题意；
故答案为：D.
【分析】由于反比例函数解析式中比例系数k=-2023＜0，故图象的两支分别分布于二，四象限，在每一个象限内，y随x的增大而增大，据此可判断A、C选项；将x=-1代入反比例函数解析式算出对应的函数值可判断B选项，当A、B两点在不同的象限的时候，即x1＜0＜x2，y1＞y2，据此可判断D选项.
4．（2023九上·汉台期末）在平面直角坐标系中，已知反比例函数y=kx的图象经过A(x1，y1)，B(2，y2)，C(3，2)，则下列说法不正确的是（ ）
A．k=6
B．函数图象位于第一、三象限
C．已知点D(2，0)，连接OB，BD，则S△OBD=3
D．若x1<2，则y1>y2
【答案】D
【知识点】坐标与图形性质；反比例函数的图象；反比例函数的性质；三角形的面积
【解析】【解答】解：∵反比例函数y=kx的图象经过C(3，2)
∴k3=2
∴k=6，即选项A正确；
∴反比例函数y=6x的图象位于第一、三象限，即选项B正确；
∵反比例函数y=kx的图象经过B(2，y2)
∴y2=62=3
∴B(2，3)
∵D(2，0)，
∴BD⊥x轴，BD=3，OD=2
∴S△OBD=12OD×BD=12×2×3=3，即选项C正确；
当0y2；当x1<0时，则y1故答案为：D.
【分析】将C（3，2）代入y=kx中可求出k的值，据此判断A；根据k的值可得反比例函数图象所在的象限，据此判断B；将B（2，y2）代入可求出y2的值，得到点B的坐标，由B、D的坐标可得BD=3，OD=2，然后根据三角形的面积公式可判断C；根据反比例函数的性质可判断D.
5．（2023九上·临湘期末）下列图象中是反比例函数y=−2x图象的是（ ）
A．B．
C．D．
【答案】C
【知识点】反比例函数的图象
【解析】【解答】解：反比例函数y=−2x图象的是C.
故答案为：C.
【分析】y=-2x中，k=-2<0，则反比例函数的图象位于二、四象限，据此判断.
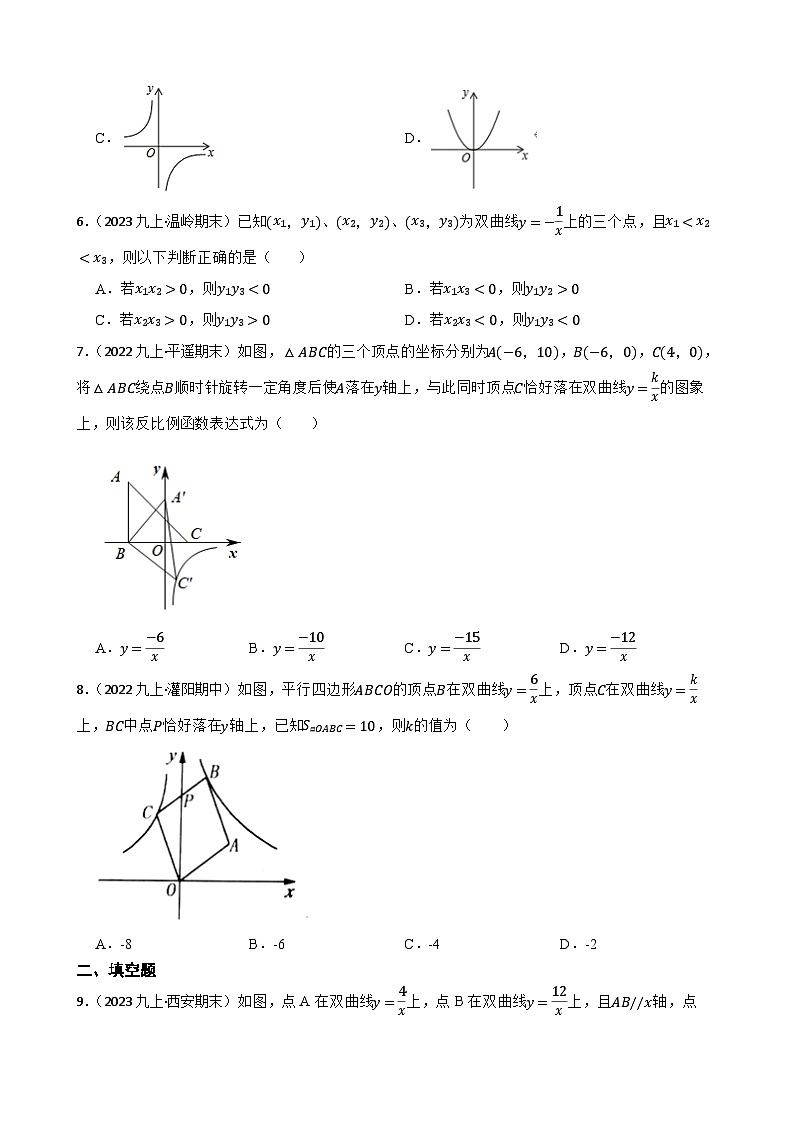
6．（2023九上·温岭期末）已知(x1，y1)、(x2，y2)、(x3，y3)为双曲线y=−1x上的三个点，且x1A．若x1x2>0，则y1y3<0B．若x1x3<0，则y1y2>0
C．若x2x3>0，则y1y3>0D．若x2x3<0，则y1y3<0
【答案】D
【知识点】反比例函数的性质；反比例函数图象上点的坐标特征
【解析】【解答】解：A、∵y=-1x，若x1x2＞0，
当x1＜x2＜x3＜0时，
∴y3＞y2＞y1＞0，
∴y1y3＞0，
∴A选项错误，不符合题意；
B、∵y=-1x，若x1x3＜0，
当x1＜0＜x2＜x3时，
∴y1＞0＞y3＞y2，
∴y1y2＜0，
∴B选项错误，不符合题意；
C、∵y=-1x，若x2x3＞0，
当x1＜0＜x2＜x3时，
∴y1＞0＞y3＞y2，
∴y1y3＜0，
∴C选项错误，不符合题意；
D、∵y=-1x，若x2x3＜0，
∴x1＜x2＜0＜x3时，
∴y2＞y1＞0＞y3，
∴y1y3＜0，
∴D选项正确，符合题意.
故答案为：D.
【分析】根据反比例函数增减性，结合每个选项条件，求得对应y的正负号，再逐项进行分析判断即可.
7．（2022九上·平遥期末）如图，△ABC的三个顶点的坐标分别为A(−6，10)，B(−6，0)，C(4，0)，将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，与此同时顶点C恰好落在双曲线y=kx的图象上，则该反比例函数表达式为（ ）
A．y=−6xB．y=−10xC．y=−15xD．y=−12x
【答案】D
【知识点】勾股定理；旋转的性质；坐标与图形变化﹣旋转；反比例函数图象上点的坐标特征
【解析】【解答】解：∵A(−6，10)，B(−6，0)，C(4，0)，
∴AB⊥x轴，AB=10，BC=10，
∴AC=102，
∵将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，
∴BA′=AB=10，BC′=BC=10，A′C′=AC=102，
在Rt△OBA′中，OA′=A′B2−OB2=102−62=8，
∴A′(0，8)，
设C′(a，b)，
∴BC′2=(a+6)2+b2=100①，A′C′2=a2+(b−8)2=200②，
①−②得b=−3a−184③，
把③代入①整理得a2+12a−28=0，解得a1=−14（舍去），a2=2，
当a=2时，b=−6，
∴C′(2，−6)，
把C′(2，−6)代入y=kx得k=2×(−6)=−12．
∴y=−12x，
故答案为：D．
【分析】利用A、B、C的坐标及勾股定理求出AC=102，由旋转的性质可得BA'=AB=10，BC′=BC=10，A′C′=AC=102，在Rt△OBA′中，利用勾股定理求出OA'，即得A’（0，8），设C′(a，b)，可得BC'2=(a+6)2+b2=100①，A′C′2=a2+(b−8)2=200②，联立①②可求出a、b值，即得C'坐标，将其代入y=kx中即可求出k值.
8．（2022九上·灌阳期中）如图，平行四边形ABCO的顶点B在双曲线y=6x上，顶点C在双曲线y=kx上，BC中点P恰好落在y轴上，已知S▱OABC=10，则k的值为（ ）
A．-8B．-6C．-4D．-2
【答案】C
【知识点】反比例函数系数k的几何意义；平行四边形的性质；反比例函数图象上点的坐标特征；三角形全等的判定（AAS）
【解析】【解答】解：连接OB，过点B作BD⊥y轴于点D，过点C作CE⊥y于点E，
∵点P是BC的中点
∴PC=PB
∵∠BDP=∠CEP=90°，∠BPD=∠CPE
∴△CPE≅△BPD
∴CE=BD
∵S▱OABC=10
∴S△OPB=S△POC=52
∵点B在双曲线y=6x上
∴S△OBD=3
∴S△BPD=S△BDP−S△OBP=12
∴S△CPE=12
∴S△OCE=S△OPC−S△CPE=2
∵点C在双曲线y=kx上
∴|k|=2S△OCE=4，k<0
∴k=−4．
故答案为：C．
【分析】连接OB，过点B作BD⊥y轴于点D，过点C作CE⊥y于点E，利用AAS证明△CPE≌△BPD，根据全等三角形的对应边相等得CE=BD，根据平行四边形的性质及同底等高的三角形面积相等得S△OPB=S△POC=52，根据反比例函数k的几何意义得S△OBD=3，从而可得S△OCE=S△OPC−S△CPE=2，最后再根据反比例函数k的几何意义结合图象所在的象限得出k的值.
二、填空题
9．（2023九上·西安期末）如图，点A在双曲线y=4x上，点B在双曲线y=12x上，且AB//x轴，点C、D在x轴上，若四边形ABCD为矩形，则它的面积为
【答案】8
【知识点】坐标与图形性质；反比例函数的图象；矩形的性质
【解析】【解答】解：设A的坐标为（a，4a）
∴AD=4a
∵四边形ABCD为矩形
∴BC=AD=4a
∴B的纵坐标为4a
∴B的横坐标为124a=3a
∴CD=3a−a=2a
∴矩形ABCD的面积=CD·AD=2a×4a=8
故答案为：8.
【分析】设A（a，4a），则AD=4a，根据矩形的性质可得BC=AD=4a，则点B的纵坐标为4a，将y=4a代入y=12x中求出x的值，得到点B的横坐标为3a，则CD=2a，接下来根据矩形的面积公式进行计算.
10．（2023九上·礼泉期末）如图，点A是反比例函数y=kx(x<0) 的图象上的一点，过点A作AB⊥x轴，垂足为B，点C 为y轴上的一点，连接AC、BC，若△ABC的面积为3，则k的值是 .
【答案】-6
【知识点】反比例函数系数k的几何意义；三角形的面积
【解析】【解答】解：连接OA，
∵AB⊥x轴，
∴∠ABO=90°=∠BOC，
∴OC∥AB，
∴S△AOB=S△ABC=3，
∴12|k|=3，
∵k＜0，
∴k=-6.
故答案为：-6
【分析】连接OA，利用同底等高的两个三角形的面积相等，可得到△AOB的面积，再根据反比例函数的几何意义，可求出k的值.
11．（2023九上·临湘期末）如果点A(−1，y1)、B(1，y2)、C(2，y3)是反比例函数y=1x图像上的三个点，则y1、y2、y3的大小关系是 .（用“<”连接）
【答案】y1【知识点】反比例函数的图象
【解析】【解答】解：把A(−1，y1)、B(1，y2)、C(2，y3)代入是反比例函数y=1x解析式得：
y1=-1；y2=1；y3=12
∴y1故答案为：y1 【分析】分别将x=-1、1、2代入反比例函数解析式中求出y1、y2、y3的值，然后进行比较.
12．（2023九上·崇左期末）如图，点A、B为直线y=x上的两点，过A、B两点分别作x轴的平行线交双曲线y=1x(x>0)于点C、D，若AC=3BD，则3OD2−OC2的值为 .
【答案】4
【知识点】坐标与图形性质；反比例函数与一次函数的交点问题；勾股定理
【解析】【解答】解：如图所示，延长CA交y轴于E，延长BD交y轴于F，
设A、B的横坐标分别是a、b，
∵点A、B为直线y=x上的两点，
∴A的坐标是(a，a)，B的坐标是(b，b)，
则AE=OE=a，BF=OF=b，
∵C、D两点在双曲线y=1x(x>0)上，
则CE=1a，DF=1b，
∴BD=BF−DF=b−1b，AC=1a−a，
∵AC=3BD，
∴1a−a=3(b−1b)，
两边平方得：a2+1a2−2=3(b2+1b2−2)，
即a2+1a2=3(b2+1b2)−4，
在直角△ODF中，
OD2=OF2+DF2=b2+1b2，
同理可得，OC2=a2+1a2，
∴3OD2−OC2=3(b2+1b2)−(a2+1a2)=4，
故答案为：4.
【分析】延长CA交y轴于E，延长BD交y轴于F，设A（a，a），B（b，b），则AE=OE=a，BF=OF=b，CE=1a，DF=1b，BD=BF-DF=b-1b，AC=1a-a，根据AC=3BD可得a2+1a2=3(b2+1b2)−4，由勾股定理可得OD2=OF2+DF2=b2+1b2，OC2=a2+1a2，据此求解.
13．（2022九上·长兴开学考）如图，四边形OABC为矩形，点A在第三象限，点A关于OB的对称点为点D，点B，D都在函数y=−32x(x<0)的图象上，BE⊥y轴于点E.若DC的延长线交y轴于点F，当矩形OABC的面积为6时，OFOE的值为 .
【答案】2
【知识点】反比例函数系数k的几何意义；平行线的性质；三角形的面积；矩形的性质；轴对称的性质
【解析】【解答】解：如图所示，分别连接BF和DO，
由对称性和矩形的性质，易得△OAB≌△BCO≌△BDO，
∴BO∥DF，
∴S△BFE=S△BDO=12S矩形OABC=3，
又∵点B在反比例函数y=-32x图象上，
∴S△BEO=322，
∴OFOE=S△BFES△BEO=3322=2.
故答案为：2.
【分析】分别连接BF和DO，由对称性和矩形的性质，易得△OAB≌△BCO≌△BDO，即得BO∥DF，从而求得△BFE的面积，再由反比例函数”k“的几何意义可得△BEO的面积，最后根据等高三角形面积之比等于底之比，代入数据计算，即可求出OFOE.
三、解答题
14．（2022九上·莲湖期末）已知反比例函数 y=2k−3x 的图象位于第二、四象限，正比例函数 y=kx 图象经过第一、三象限，求k的整数值．
【答案】解： 反比例函数 y=2k−3x 的图象位于第二、四象限，正比例函数 y=kx 图象经过第一、三象限，
∴2k-3＜0k＞0
解之：k＜32k＞0
∴k的取值范围是0＜k＜32，
∴k的整数值为1.
【知识点】反比例函数的性质；一次函数图象、性质与系数的关系
【解析】【分析】利用反比例函数y=kx（k≠0）的图象分支在第二、四象限，则k＜0；正比例函数y=kx（k≠0）的图象经过第一、三象限，可知k＞0；由此可得到关于k的不等式组，然后求出不等式组的解集，利用不等式组的解集可得到k的整数值.
15．（2022九上·莲湖期末）如图所示，矩形AOBC的边AO，OB在两坐标轴上，双曲线 y=8x 与矩形AOBC的边交于点D，E，点C（8，5），求D，E两点的坐标．
【答案】解：∵矩形ABCD，点C（8，5）
∴AC∥x轴，BC∥y轴，
∵点D，E在反比例 y=8x的图象上，
∴当y=5时，
5x=8
解之：x=85
∴点D(85，5)；
当x=8时，8y=8，
解之：y=1
∴点E（8，1）.
【知识点】矩形的性质；反比例函数图象上点的坐标特征
【解析】【分析】利用矩形的性质可证得AC∥x轴，BC∥y轴，由点D，E在反比例 y=8x的图象上，可求出当y=5时的x的值，可得到点D的坐标，再求出当x=8时y的值，可得到点E的坐标.
四、综合题
16．（2023九上·礼泉期末）如图，一次函数y=kx+b与反比例函数y=m/x的图象相交于A、B两点，过点B作BC⊥x轴，垂足为C，连接AC，已知A点的坐标是(2，3)，BC=2.
（1）求反比例函数与一次函数的关系式；
（2）点P为反比例函数y=m/x图象上的任意一点，若S_POC=3S_ABC，求点P的坐标.
【答案】（1）解：∵反比例函数 y=mx 过点A(2，3)，
∴m=2×3=6.
∴反比例函数的关系式为 y=6x.
∵BC=2，∴B的纵坐标为-2，
代入得， −2=6x，
解得x=-3，
∴B(-3，-2)，
∵A(2，3)，B(-3，-2)两点在y=kx+b上，
∴2k+b=3，−3k+b=−2， 解得： k=1b=1，
∴一次函数的关系式为：y=x+1.
（2）解：∵ BC=2，
∴SABC=12×2×5=5，∴SPOC=3SABC=15.
∴SPOC=12OC⋅|yP|=15， 即 12×3×|yP|=15，
∴|yP|=10，
当点P的纵坐标为10时，则 10=6x， 解得 x=35，
当点P的纵坐标为-10时，则 −10=6x， 解得 x=−35，
∴点P的坐标为 (35，10) 或 (−35，−10).
【知识点】待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题；三角形的面积
【解析】【分析】（1）将点A的坐标代入反比例函数解析式，可求出m的值，可得到反比例函数解析式；由此可求出点B的坐标，将点A，B的坐标代入一次函数解析式，可得到关于k，b的方程组，解方程组求出k，b的值，可得到函数解析式.
（2）利用BC的长和三角形的面积公式求出△ABC的面积，即可得到△POC的面积；利用△POC的面积，可求出点P的纵坐标，据此可求出点P的横坐标，即可得到点P的坐标.
17．（2022九上·长沙月考）在平面直角坐标系内，已知任意两点的坐标A(x1，y1)，B(x2，y2)，我们把|x1−x2|称为A、B两点的“横向距离”，记作AB=|x1−x2|.例如：A(7，12)，B(5，6)，则AB=|7−5|=2.
（1）①若点A(x1，2)，B(x2，−6)，当A、B都在函数y=2x+4的函数图象上时，AB= .
②若点A(x1，2)，B(x2，−4)，当A、B都在函数y=−8x的函数图象上时，AB= .
（2）已知直线y=−x+b（b>0）交x轴于B点，交y轴于A点，在第一象限内交双曲线y=kx(k>0)于C，D两点，且满足AC=CD=BD.若k−b+18≥m恒成立，求m的最大值.
（3）若抛物线y=ax2+bx+c(a≠0)与直线y=ax+b(b≠0)在同一坐标平面内交于A(x1，y1)，B(x2，y2)，且满足下列两个条件：①a>b>c，②抛物线过(1，0)，试求AB的取值范围.
【答案】（1）4；6
（2）解：直线y=−x+b，当x=0时，y=b，当y=0时，x=b，
∴A(0，b)，B(b，0)，
∵AC=CD=BD，
∴C，D是AB的三等分点，
∴C(13b，23b)，D(23b，13b)
∵点C和点D在反比例函数y=kx(k>0) 的图象上，
∴k=13b⋅23b=29b2 ，
∴k−b+18=29b2−b+18=29(b−94)2−1≥−1
∵k−b+18≥m 恒成立，
∴m<−1；
（3）解：联立y=ax2+bx+cy=ax+b 得∶ax2+(b−a)x+c−b=0，
∵抛物线与直线交点为A(x1，y1)，B(x2，y2)，
∴x1+x2=a−ba，x1⋅x2=c−ba
∴AB2=(x1+x2)2−4x1x2=(a−ba)2−4×(c−ba)
=1−2ba+(ba)2−4ca+4ba
=1+2ba+(ba)2−4ca；
∵抛物线经过点(1，0)，
∴a+b+c=0，
∴c=−a−b，
∴AB2=1+2ba+(ba)2−4(−a−b)a=(ba)2+6ba+5=(ba+3)2−4；
∵a>b>c，
∴b>−a−b，解得：b>−a2；
∴−a2∴−12∵AB2=(ba+3)2−4，
对称轴为ba=−3，
∴−12当ba=−12时，AB2=(−12+3)2−4=94，AB=AB2=32；
当ba=1时，AB2=(1+3)2−4=12，AB=AB2=23；
∴32【知识点】反比例函数与一次函数的交点问题
【解析】【解答】（1）解：①当y=2时，2=2x+4，解得：x=−1；
当y=−6时，−6=2x+4，解得：x=−5；
∴A(−1，2)，B(−5，−6)，
∴AB=|−1−(−5)|=4；
故答案为：4；
②当y=2时，2=−8x，解得：x=−4；当y=−4时，−4=−8x，解得：x=2；
∴A(−4，2)，B(2，−4)，
∴AB=|−4−2|=6；
故答案为：6；
【分析】（1）①将A、B两点的纵坐标分别代入y=2x+4算出对应的自变量x的值，求出A、B两点的坐标，进而根据 “横向距离” 的定义求解即可；②将A、B两点的纵坐标分别代入 y=−8x 算出对应的自变量x的值，求出A、B两点的坐标，进而根据 “横向距离” 的定义求解即可；
（2）分别令解析式y=-x+b中的x=0与y=0，算出对应的y与x的值，可得A、B两点的坐标，由题意易得C、D是AB的三等分点，据此用含b的式子表示出C、D的坐标，进而根据反比例函数图象上任意一点的横纵坐标的乘积等于定值k，用含b的式子表示出k，再代入已知不等式，利用配方法及偶数次幂的非负性即可得出答案；
（3）联立抛物线与一次函数的解析式可得关于x的一元二次方程 ，根据根与系数的关系可得a、b、c之间的关系 ，进而根据“横向距离” 的定义表示出 AB2，然后根据条件①和条件②列出不等式，解不等式得到 AB 的取值范围．