






还剩33页未读,
继续阅读
第23章《图形的相似》单元复习 华东师大版九年级数学上册课件
展开
这是一份第23章《图形的相似》单元复习 华东师大版九年级数学上册课件,共41页。
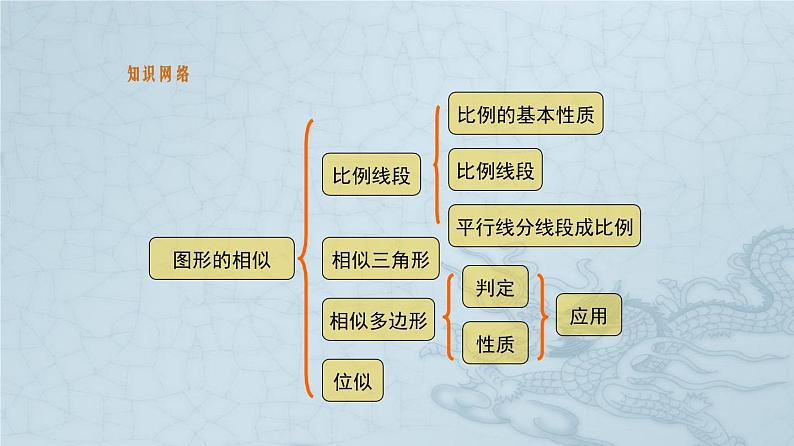
九年级上册 第四章 图形的相似 知识网络图形的相似比例线段相似三角形相似多边形位似比例的基本性质比例线段平行线分线段成比例判定性质应用 如果选用一个长度单位量得两条线段a ,b 的长度分别为m ,n .那么两条线段的比 . 四条线段a , b , c , d中,如果a与b的比等于c与d的比,那么这四条线段a , b , c , d叫做成比例线段,简称比例线段.要点归纳比例的基本性质─比例的合比性质─比例的等比性质─比例的更比性质— 那么称线段AB被点C点C叫做线段AB的AC与AB(或BC与AC)的比叫做黄金比≈0.618黄金分割黄金分割点黄金比1.定义: 三角对应角相等、三边对应成比例的两个三角形叫相似三角形.2.判定定理: (1)两角相等的两个三角形相似 (2)三边对应成比例的两个三角形相似 (3)两边对应成比例且夹角相等的两个三角形相似3.性质: (1)相似三角形对应角相等,对应边成比例 (2)相似三角形对应高的比,对应角平分线的比和对应中线的 比都等于相似比★相似三角形周长的比等于 相似比 ★相似三角形面积的比等于 相似比的平方★相似多边形的周长比等于 相似比★相似多边形面积的比等于 相似比的平方 如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.★这个点叫做位似中心.★这两个相似图形的相似比又称为位似比.★位似图形上任意一对对应点到位似中心的距离之比等于位似比.3.体会位似图形何时为正像何时为倒像.2.如何作位似图形(缩小).1.如何作位似图形(放大).例1 在比例尺为1∶200的地图上,测得A,B两地间的图上距离为4.5 cm,则A,B两地间的实际距离为__________m.【解析】设A,B两地间的实际距离为x cm,则即x=900,又900 cm=9 m.答案:9典例精析例2 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.(1)求证:△ABD∽△CED;(2)若AB=6,AD=2CD,求BE的长.解:(1)∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,∠ACF=120°.∵CE是外角平分线,∴∠ACE=60°.∴∠BAC=∠ACE.又∵∠ADB=∠CDE,∴△ABD∽△CED.(2)作BM⊥AC于点M,AC=AB=6.∴AM=CM=3,∵AD=2CD,∴CD=2,AD=4,MD=1.在Rt△BDM中, .由(1)△ABD∽△CED得, 例3 小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2 m,CE=0.8 m,CA=30 m(点A、E、C在同一直线上).已知小明的身高EF是1.7 m,请你帮小明求出楼高AB(结果精确到0.1 m).解:过点D作DG⊥AB,分别交AB、EF于点G、H,则EH=AG=CD=1.2 m,DH=CE=0.8 m,DG=CA=30 m.因为EF和AB都垂直于地面,所以EF∥AB,所以∠BGD=∠FHD=90°,∠GBD=∠HFD,所以△BDG∽△FDH.所以由题意,知FH=EF-EH=1.7-1.2=0.5(m). 解得BG=18.75(m).∴AB=BG+AG=18.75+1.2=19.95≈20.0(m).∴楼高AB约为20.0 m.1.四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,则 a= 2.四个正数a、b、c、d能构成比例式,其中b=3,c=2,d=6,则a= . 3.若则14或9或1当堂练习4.若线段MN=10,点K为MN的黄金分割点,则KM的长为 .5.如图,在△ABC中,已知DE//BC,AD=3BD,S△ABC=48,求S△ADE.ABCDE31解:∵ DE∥BC, ∴△ADE∽△ABC. ∴S△ABC : S△ADE = ∵AD : BD = 1:3, ∴AD : AB = 1:4. ∴S△ADE=27. 6.如图,将矩形ABCD沿两条较长边的中点的连线对折,得到的矩形ADFE与矩形ABCD相似,确定矩形ABCD长与宽的比.ABCDEF解:矩形ADFE与矩形ABCD 相似, 7.如图,在长8cm、宽6cm的矩形中,截去一个矩形(图中阴影部分所示),使留下的矩形与原矩形相似,那么留下的矩形面积为多少?由题意得解:设留下矩形的面积为 x cm2,解得 x =27 cm2.答:留下矩形的面积为 27 cm2.8.如图,△ABC是一张锐角三角形的硬纸片.AD是边BC上的高,BC=40,AD=30.从这张硬纸片剪下一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M. (1)求证: ; (2)求这个矩形EFGH的周长. (1)证明:∵矩形EFGH,∴EF∥GH. ∴解:(2)设矩形的宽HE = x,则MD = HE = x ∵AD = 30, ∴AM = 30 – x . ∵HG = 2HE, ∴HG = 2x . ∵ ∴ ∴x = 12. ∴HE = 12, HG = 24. ∴矩形EFGH的周长=2(HE + HG)=2(12+24)= 72.9.请用点O为位似中心画出△ABC各边同时扩大2倍的位似△A′B′C′.1.(1)已知 ,那么 = , = . (3)如果 ,那么 . (2)如果 那么 .补充练习3. 如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1. (1) 求BC长;解:∵ E 是 AD 的中点,又∵矩形 ABCD 与矩形 EABF相似,AB=1, (2) 求矩形 ABEF 与矩形 ABCD 的相似比.解:矩形 ABEF 与矩形 ABCD 的相似比为:4. 如图,在 □ABCD 中,EF∥AB, DE : EA = 2 : 3, EF = 4,求 CD 的长. 解:∵ EF∥AB,DE : EA = 2 : 3,∴ △DEF ∽ △DAB,解得 AB = 10.又 ∵ 四边形 ABCD 为平行四边形,∴ CD = AB = 10.5. 如图,已知菱形 ABCD 内接于△AEF,AE=5cm, AF = 4 cm,求菱形的边长. 解:∵ 四边形 ABCD 为菱形,∴CD∥AB,设菱形的边长为 x cm,则CD = AD = x cm,DF = (4-x) cm,6. 如图,△ABC中,点 D,E,F 分别是 AB,BC,CA 的中点,求证:△ABC∽△EFD.∴ △ABC∽△EFD.证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,7. 如图,某地四个乡镇 A,B,C,D 之间建有公路, 已知 AB = 14 千米,AD = 28 千米,BD = 21 千米, DC = 31.5 千米,公路 AB 与 CD 平行吗?说出你 的理由.解:公路 AB 与 CD 平行.∴ △ABD∽△BDC,∴∠ABD=∠BDC,∴AB∥DC.证明: ∵ △ABC 的高AD、BE交于点F,∴ ∠FEA=∠FDB=90°,∠AFE =∠BFD (对顶角相等).∴ △FEA ∽ △ FDB,∴1. 如图,△ABC 的高 AD、BE 交于点 F. 求证: 课后练习证明:∵∠BAC= ∠1+ ∠DAC,∠DAE= ∠3+ ∠DAC,∠1=∠3,∴ ∠BAC=∠DAE.∵ ∠C=180°-∠2-∠DOC ,∠E=180°-∠3-∠AOE,∠DOC =∠AOE(对顶角相等),∴ ∠C= ∠E.∴ △ABC∽△ADE.2. 如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.3. 如图,这是圆桌正上方的灯泡 (点A) 发出的光线照 射桌面形成阴影的示意图,已知桌面的直径为 1.2 米,桌面距离地面为 1 米,若灯泡距离地面 3 米, 则地面上阴影部分的面积约为多少 (结果保留两位 小数)?解:∵ FH = 1 米,AH = 3 米,桌面的直径为 1.2 米, ∴ AF = AH-FH = 2 (米),DF = 1.2÷2 = 0.6 (米). ∵DF∥CH, ∴△ADF ∽△ACH,解得 CH = 0.9米.∴ 阴影部分的面积为:答:地面上阴影部分的面积为 2.54 平方米.4. △ABC 中,DE∥BC,EF∥AB,已知 △ADE 和 △EFC 的面积分别为 4 和 9,求 △ABC 的面积.解:∵ DE∥BC,EF∥AB,∴ △ADE ∽△ABC,∠ADE =∠EFC,∠A =∠CEF,∴△ADE ∽△EFC.又∵S△ADE : S△EFC = 4 : 9,∴ AE : EC=2:3,则 AE : AC =2 : 5,∴ S△ADE : S△ABC = 4 : 25,∴ S△ABC = 25.5. 如图,△ABC 中,DE∥BC,DE 分别交 AB、AC 于 点 D、E,S△ADE=2 S△DCE,求 S△ADE ∶S△ABC.解:过点 D 作 AC 的垂线,交点为 F,则又∵ DE∥BC,∴ △ADE ∽△ABC.F即 S△ADE : S△ABC =4 : 9.F6. 如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆 AB 的高度,他们通过调整测量位置,使斜边 DF 与地面保持平行,并使边DE 与旗杆顶点 A 在同一直线上,已知 DE = 0.5 米,EF = 0.25 米,目测点 D 到地面的距离 DG = 1.5 米,到旗杆的水平距离 DC = 20 米,求旗杆的高度.解:由题意可得:△DEF∽△DCA,∵DE=0.5米,EF=0.25米,DG=1.5米,DC=20米,解得:AC = 10,故 AB = AC + BC = 10 + 1.5 = 11.5 (m).答:旗杆的高度为 11.5 m.7. 如图,某一时刻,旗杆 AB 的影子的一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB 在地面上的影长 BC 为 9.6 m,在墙面上的影长 CD 为 2 m.同一时刻,小明又测得竖立于地面长 1 m 的标杆的影长为 1.2 m.请帮助小明求出旗杆的高度.解:如图:过点 D 作 DE∥BC,交 AB 于点 E,∴ DE = CB = 9.6 m,BE = CD = 2 m,∵ 在同一时刻物高与影长成正比例,∴ EA : ED=1 : 1.2,∴ AE = 8 m,∴ AB = AE + EB = 8 + 2 = 10 (m),∴ 学校旗杆的高度为 10 m.
九年级上册 第四章 图形的相似 知识网络图形的相似比例线段相似三角形相似多边形位似比例的基本性质比例线段平行线分线段成比例判定性质应用 如果选用一个长度单位量得两条线段a ,b 的长度分别为m ,n .那么两条线段的比 . 四条线段a , b , c , d中,如果a与b的比等于c与d的比,那么这四条线段a , b , c , d叫做成比例线段,简称比例线段.要点归纳比例的基本性质─比例的合比性质─比例的等比性质─比例的更比性质— 那么称线段AB被点C点C叫做线段AB的AC与AB(或BC与AC)的比叫做黄金比≈0.618黄金分割黄金分割点黄金比1.定义: 三角对应角相等、三边对应成比例的两个三角形叫相似三角形.2.判定定理: (1)两角相等的两个三角形相似 (2)三边对应成比例的两个三角形相似 (3)两边对应成比例且夹角相等的两个三角形相似3.性质: (1)相似三角形对应角相等,对应边成比例 (2)相似三角形对应高的比,对应角平分线的比和对应中线的 比都等于相似比★相似三角形周长的比等于 相似比 ★相似三角形面积的比等于 相似比的平方★相似多边形的周长比等于 相似比★相似多边形面积的比等于 相似比的平方 如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.★这个点叫做位似中心.★这两个相似图形的相似比又称为位似比.★位似图形上任意一对对应点到位似中心的距离之比等于位似比.3.体会位似图形何时为正像何时为倒像.2.如何作位似图形(缩小).1.如何作位似图形(放大).例1 在比例尺为1∶200的地图上,测得A,B两地间的图上距离为4.5 cm,则A,B两地间的实际距离为__________m.【解析】设A,B两地间的实际距离为x cm,则即x=900,又900 cm=9 m.答案:9典例精析例2 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.(1)求证:△ABD∽△CED;(2)若AB=6,AD=2CD,求BE的长.解:(1)∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,∠ACF=120°.∵CE是外角平分线,∴∠ACE=60°.∴∠BAC=∠ACE.又∵∠ADB=∠CDE,∴△ABD∽△CED.(2)作BM⊥AC于点M,AC=AB=6.∴AM=CM=3,∵AD=2CD,∴CD=2,AD=4,MD=1.在Rt△BDM中, .由(1)△ABD∽△CED得, 例3 小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2 m,CE=0.8 m,CA=30 m(点A、E、C在同一直线上).已知小明的身高EF是1.7 m,请你帮小明求出楼高AB(结果精确到0.1 m).解:过点D作DG⊥AB,分别交AB、EF于点G、H,则EH=AG=CD=1.2 m,DH=CE=0.8 m,DG=CA=30 m.因为EF和AB都垂直于地面,所以EF∥AB,所以∠BGD=∠FHD=90°,∠GBD=∠HFD,所以△BDG∽△FDH.所以由题意,知FH=EF-EH=1.7-1.2=0.5(m). 解得BG=18.75(m).∴AB=BG+AG=18.75+1.2=19.95≈20.0(m).∴楼高AB约为20.0 m.1.四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,则 a= 2.四个正数a、b、c、d能构成比例式,其中b=3,c=2,d=6,则a= . 3.若则14或9或1当堂练习4.若线段MN=10,点K为MN的黄金分割点,则KM的长为 .5.如图,在△ABC中,已知DE//BC,AD=3BD,S△ABC=48,求S△ADE.ABCDE31解:∵ DE∥BC, ∴△ADE∽△ABC. ∴S△ABC : S△ADE = ∵AD : BD = 1:3, ∴AD : AB = 1:4. ∴S△ADE=27. 6.如图,将矩形ABCD沿两条较长边的中点的连线对折,得到的矩形ADFE与矩形ABCD相似,确定矩形ABCD长与宽的比.ABCDEF解:矩形ADFE与矩形ABCD 相似, 7.如图,在长8cm、宽6cm的矩形中,截去一个矩形(图中阴影部分所示),使留下的矩形与原矩形相似,那么留下的矩形面积为多少?由题意得解:设留下矩形的面积为 x cm2,解得 x =27 cm2.答:留下矩形的面积为 27 cm2.8.如图,△ABC是一张锐角三角形的硬纸片.AD是边BC上的高,BC=40,AD=30.从这张硬纸片剪下一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M. (1)求证: ; (2)求这个矩形EFGH的周长. (1)证明:∵矩形EFGH,∴EF∥GH. ∴解:(2)设矩形的宽HE = x,则MD = HE = x ∵AD = 30, ∴AM = 30 – x . ∵HG = 2HE, ∴HG = 2x . ∵ ∴ ∴x = 12. ∴HE = 12, HG = 24. ∴矩形EFGH的周长=2(HE + HG)=2(12+24)= 72.9.请用点O为位似中心画出△ABC各边同时扩大2倍的位似△A′B′C′.1.(1)已知 ,那么 = , = . (3)如果 ,那么 . (2)如果 那么 .补充练习3. 如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1. (1) 求BC长;解:∵ E 是 AD 的中点,又∵矩形 ABCD 与矩形 EABF相似,AB=1, (2) 求矩形 ABEF 与矩形 ABCD 的相似比.解:矩形 ABEF 与矩形 ABCD 的相似比为:4. 如图,在 □ABCD 中,EF∥AB, DE : EA = 2 : 3, EF = 4,求 CD 的长. 解:∵ EF∥AB,DE : EA = 2 : 3,∴ △DEF ∽ △DAB,解得 AB = 10.又 ∵ 四边形 ABCD 为平行四边形,∴ CD = AB = 10.5. 如图,已知菱形 ABCD 内接于△AEF,AE=5cm, AF = 4 cm,求菱形的边长. 解:∵ 四边形 ABCD 为菱形,∴CD∥AB,设菱形的边长为 x cm,则CD = AD = x cm,DF = (4-x) cm,6. 如图,△ABC中,点 D,E,F 分别是 AB,BC,CA 的中点,求证:△ABC∽△EFD.∴ △ABC∽△EFD.证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,7. 如图,某地四个乡镇 A,B,C,D 之间建有公路, 已知 AB = 14 千米,AD = 28 千米,BD = 21 千米, DC = 31.5 千米,公路 AB 与 CD 平行吗?说出你 的理由.解:公路 AB 与 CD 平行.∴ △ABD∽△BDC,∴∠ABD=∠BDC,∴AB∥DC.证明: ∵ △ABC 的高AD、BE交于点F,∴ ∠FEA=∠FDB=90°,∠AFE =∠BFD (对顶角相等).∴ △FEA ∽ △ FDB,∴1. 如图,△ABC 的高 AD、BE 交于点 F. 求证: 课后练习证明:∵∠BAC= ∠1+ ∠DAC,∠DAE= ∠3+ ∠DAC,∠1=∠3,∴ ∠BAC=∠DAE.∵ ∠C=180°-∠2-∠DOC ,∠E=180°-∠3-∠AOE,∠DOC =∠AOE(对顶角相等),∴ ∠C= ∠E.∴ △ABC∽△ADE.2. 如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.3. 如图,这是圆桌正上方的灯泡 (点A) 发出的光线照 射桌面形成阴影的示意图,已知桌面的直径为 1.2 米,桌面距离地面为 1 米,若灯泡距离地面 3 米, 则地面上阴影部分的面积约为多少 (结果保留两位 小数)?解:∵ FH = 1 米,AH = 3 米,桌面的直径为 1.2 米, ∴ AF = AH-FH = 2 (米),DF = 1.2÷2 = 0.6 (米). ∵DF∥CH, ∴△ADF ∽△ACH,解得 CH = 0.9米.∴ 阴影部分的面积为:答:地面上阴影部分的面积为 2.54 平方米.4. △ABC 中,DE∥BC,EF∥AB,已知 △ADE 和 △EFC 的面积分别为 4 和 9,求 △ABC 的面积.解:∵ DE∥BC,EF∥AB,∴ △ADE ∽△ABC,∠ADE =∠EFC,∠A =∠CEF,∴△ADE ∽△EFC.又∵S△ADE : S△EFC = 4 : 9,∴ AE : EC=2:3,则 AE : AC =2 : 5,∴ S△ADE : S△ABC = 4 : 25,∴ S△ABC = 25.5. 如图,△ABC 中,DE∥BC,DE 分别交 AB、AC 于 点 D、E,S△ADE=2 S△DCE,求 S△ADE ∶S△ABC.解:过点 D 作 AC 的垂线,交点为 F,则又∵ DE∥BC,∴ △ADE ∽△ABC.F即 S△ADE : S△ABC =4 : 9.F6. 如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆 AB 的高度,他们通过调整测量位置,使斜边 DF 与地面保持平行,并使边DE 与旗杆顶点 A 在同一直线上,已知 DE = 0.5 米,EF = 0.25 米,目测点 D 到地面的距离 DG = 1.5 米,到旗杆的水平距离 DC = 20 米,求旗杆的高度.解:由题意可得:△DEF∽△DCA,∵DE=0.5米,EF=0.25米,DG=1.5米,DC=20米,解得:AC = 10,故 AB = AC + BC = 10 + 1.5 = 11.5 (m).答:旗杆的高度为 11.5 m.7. 如图,某一时刻,旗杆 AB 的影子的一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB 在地面上的影长 BC 为 9.6 m,在墙面上的影长 CD 为 2 m.同一时刻,小明又测得竖立于地面长 1 m 的标杆的影长为 1.2 m.请帮助小明求出旗杆的高度.解:如图:过点 D 作 DE∥BC,交 AB 于点 E,∴ DE = CB = 9.6 m,BE = CD = 2 m,∵ 在同一时刻物高与影长成正比例,∴ EA : ED=1 : 1.2,∴ AE = 8 m,∴ AB = AE + EB = 8 + 2 = 10 (m),∴ 学校旗杆的高度为 10 m.
相关资料
更多









