2023九年级数学上册第23章图形的相似全章综合检测作业课件新版华东师大版

这是一份2023九年级数学上册第23章图形的相似全章综合检测作业课件新版华东师大版，共26页。

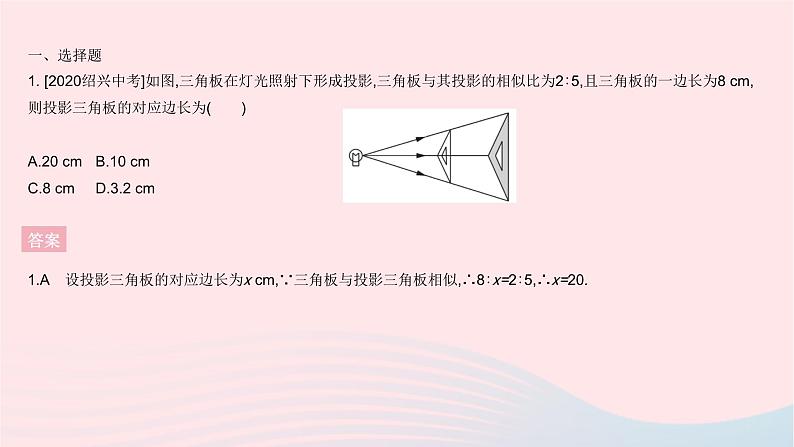
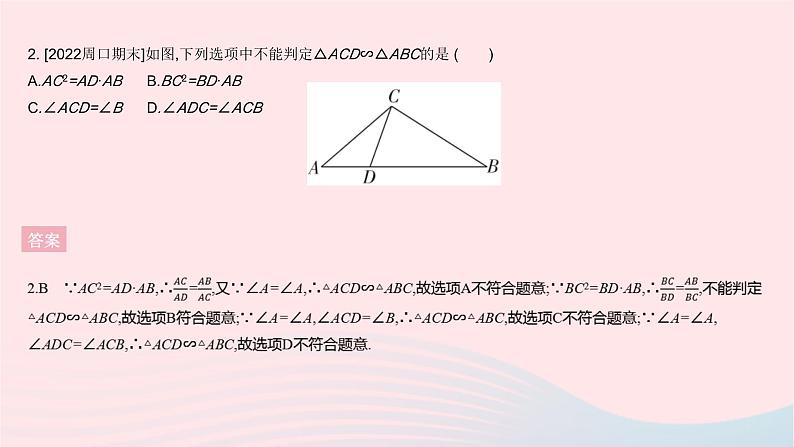
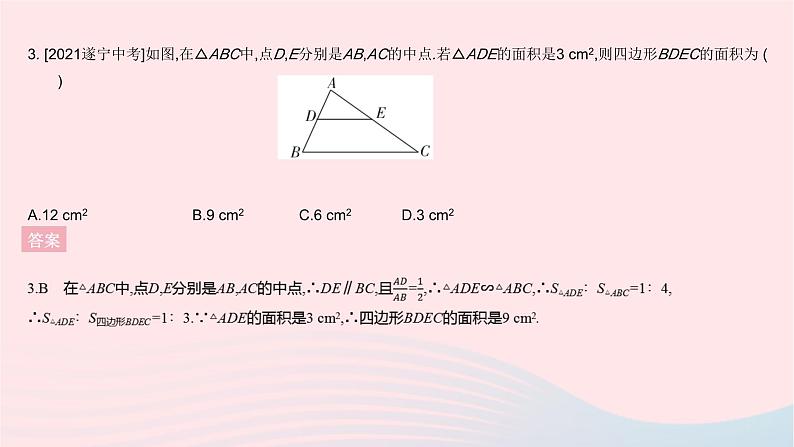
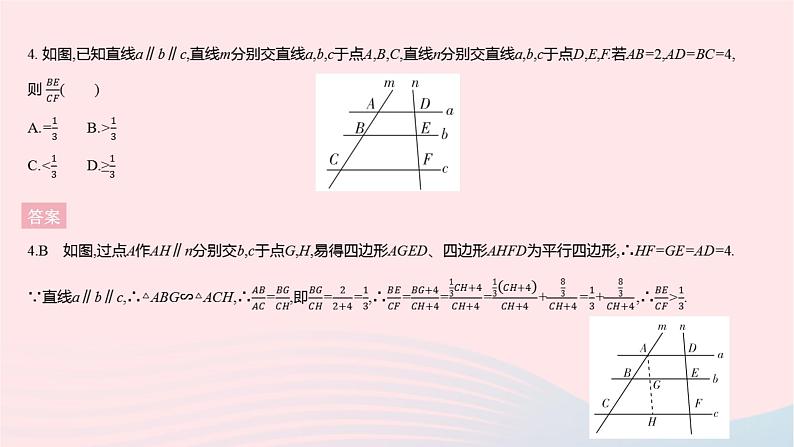
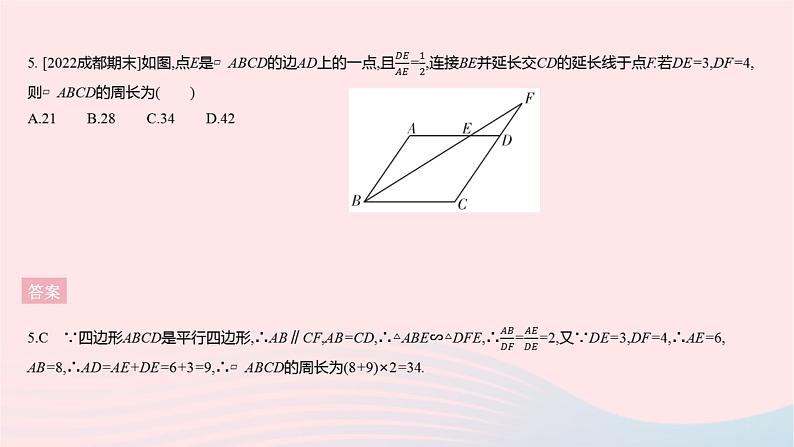
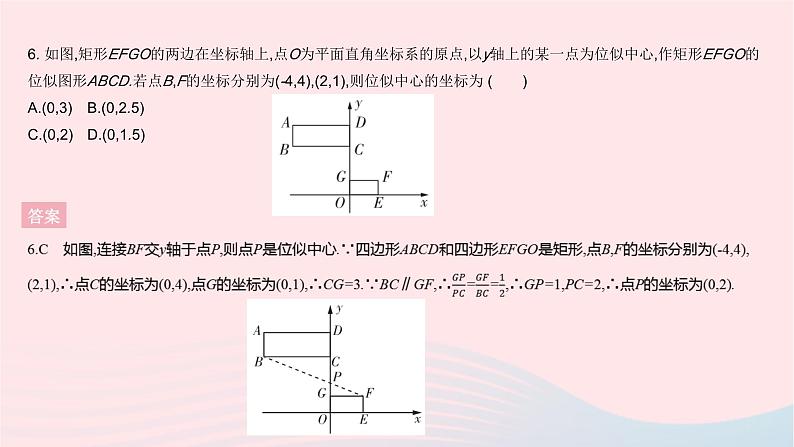
全章综合检测一、选择题1. [2020绍兴中考]如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2∶5,且三角板的一边长为8 cm,则投影三角板的对应边长为(　　)　　　　　 　　　　　　　　　　A.20 cm B.10 cmC.8 cm D.3.2 cm答案1.A　设投影三角板的对应边长为x cm,∵三角板与投影三角板相似,∴8∶x=2∶5,∴x=20.2. [2022周口期末]如图,下列选项中不能判定△ACD∽△ABC的是 (　　)A.AC2=AD·AB B.BC2=BD·ABC.∠ACD=∠B D.∠ADC=∠ACB答案 3. [2021遂宁中考]如图,在△ABC中,点D,E分别是AB,AC的中点.若△ADE的面积是3 cm2,则四边形BDEC的面积为 (　　)A.12 cm2 B.9 cm2 C.6 cm2 D.3 cm2答案  答案  答案 6. 如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作矩形EFGO的位似图形ABCD.若点B,F的坐标分别为(-4,4),(2,1),则位似中心的坐标为 (　　)A.(0,3) B.(0,2.5)C.(0,2) D.(0,1.5)答案 7. [2022天津滨海新区期中]如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是 (　　)A.AC=DE B.BC=EFC.∠AEF=∠D D.AB⊥DF答案  答案  答案 10. 2021年4月8日,中国扬州世界园艺博览会在扬州仪征市开幕,本届博览会以“绿色城市,健康生活”为主题.如图是扬州世界园艺博览会部分导游图,若滩涂印象的坐标为(2,1),丛林野趣的坐标为(-3,-2),则中国馆的坐标为　　　　. 答案10.(3,-2)　因为滩涂印象的坐标为(2,1),丛林野趣的坐标为(-3,-2),所以建立平面直角坐标系如下,则中国馆的坐标为(3,-2).11. [2021泰州中考]如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P,M,N分别是AD,BD,AC的中点.设△PMN的面积为S,则S的范围是　　　　. 答案 12. [2020金华中考]图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1 cm,AC=BD=6 cm, CE=DF, CE∶AE=2∶3.按图示方式用手指按夹子,夹子两边绕点O转动.(1)当E,F两点的距离最大时,以A,B,C,D为顶点的四边形的周长是　　　　cm. (2)当夹子的开口最大(即点C与点D重合)时,A,B两点的距离为　　　　cm.  答案三、解答题13. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(2,-1),B(1,-2),C(3,-3).(1)将△ABC向上平移4个单位得到△A1B1C1,请画出△A1B1C1;(点A,B,C的对应点分别为点A1,B1,C1)(2)请画出与△ABC关于y轴对称的△A2B2C2;(点A,B,C的对应点分别为点A2,B2,C2)(3)请写出点A1,A2的坐标.13.解:(1)如图,△A1B1C1即所求.(2)如图,△A2B2C2即所求.(3)A1(2,3),A2(-2,-1).答案14. 如图,小华和同伴春游时,发现在某地小山坡的点E处有一棵小桃树,他们想利用皮尺、测角仪和平面镜测量小桃树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且测得BC=6米,CD=24米,∠CDE=135°.已知小华的眼睛距地面的高度AB=1.5米,请根据以上数据,求DE的长度.(结果保留根号) 答案  答案  16 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位,当点P运动到点C时,两点都停止运动.设运动时间为t秒.(1)求线段CD的长.(2)设△CPQ的面积为S,求S与t之间的函数表达式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ∶S△ABC=9∶100.若存在,求出t的值;若不存在,请说明理由.(3)是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,请说明理由. 答案