人教版八年级上册11.3.2 多边形的内角和教学课件ppt

这是一份人教版八年级上册11.3.2 多边形的内角和教学课件ppt，共14页。PPT课件主要包含了归纳整理，三角形等内容，欢迎下载使用。

11.3.2 多边形的内角和(第2课时)
理解多边形内角和被180整除，能解决缺角内角和问题。能求凹多边形的内角和。运用多边形的内角和、外角和建立方程，体会整体思想。
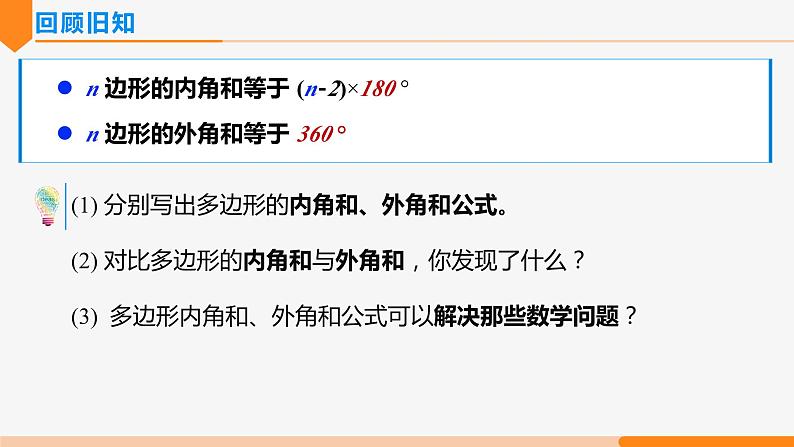
(1) 分别写出多边形的内角和、外角和公式。(2) 对比多边形的内角和与外角和，你发现了什么？(3) 多边形内角和、外角和公式可以解决那些数学问题？
n 边形的内角和等于 (n-2)×180 °
n 边形的外角和等于 360 °
1. 已知正多边形的每个内角都是156°，求这个多边形的边数．
解法1： 设这个多边形的边数为n，由题意得(n－2)×180°＝156°×n，解得 n＝15，即这个多边形的边数为15.
解法2： 设这个多边形的边数为n，由题意得(180°－156°)×n＝360°，解得 n＝15，即这个多边形的边数为15.
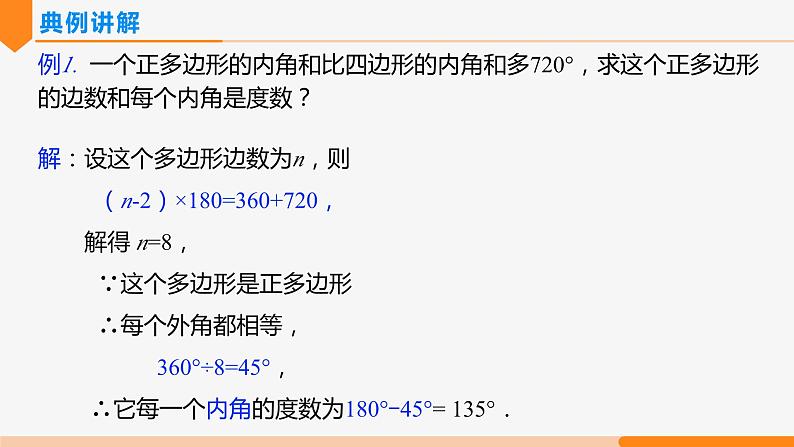
例1. 一个正多边形的内角和比四边形的内角和多720°，求这个正多边形的边数和每个内角是度数？
解：设这个多边形边数为n，则（n-2）×180=360+720， 解得 n=8，∵这个多边形是正多边形 ∴每个外角都相等， 360°÷8=45°， ∴它每一个内角的度数为180°-45°= 135°．
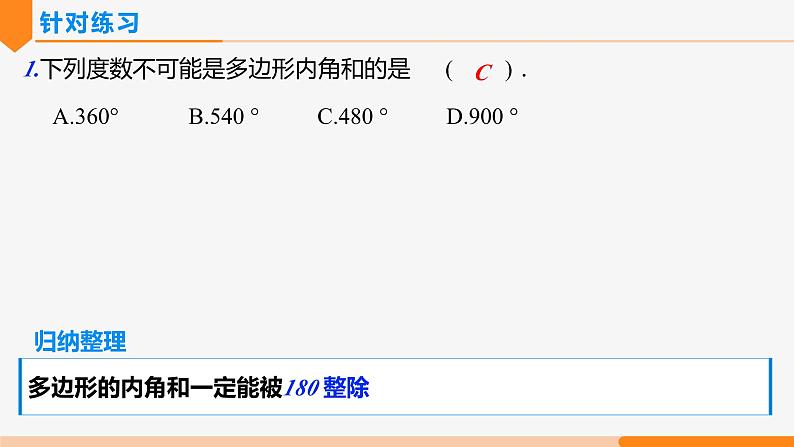
1.下列度数不可能是多边形内角和的是 ( )．A.360° B.540 ° C.480 ° D.900 °
多边形的内角和一定能被180 整除
例2. 一个同学在进行多边形的内角和计算时，求得内角和为1125°，当他发现错了以后，重新检查，发现少算了一个内角，问这个内角是多少度？他求的是几边形的内角和？
解：设此多边形的少算了的内角为 a 度，边数为 n,则有：1125°÷180°=6……45°∵ 多边形的内角和一定是180°的倍数，∴ 少算了的内角为 a=180°-45°＝135°（n-2）×180°=1125°+135°，解之得：n＝9.综上所得：漏加的这个内角是135°，这个多边形是九边形．
解：∵∠EAB+∠ABC+∠C+∠D+∠E=540°，∠C=100°，∠D=75°，∠E=135°，∴∠EAB+∠ABC=540°-∠C-∠D-∠E=230°.∵AP平分∠EAB,∴∠PAB＝ ∠EAB，同理可得∠ABP＝ ∠ABC，在△ABC中
∵∠P+∠PAB+∠PBA=180°，∴∠P=180°-∠PAB-∠PBA=180°− ( ∠EAB+∠ABC )=180°− ×230°=65°．
例3. 如图，在五边形ABCDE中，∠C=100°，∠D=75°，∠E=135°，AP平分∠EAB，BP平分∠ABC，求∠P的度数．
例4. 已知如图1，线段AB，CD相交于O点，连接AD，CB，我们把如图1的图形称之为“8字形”．那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：(1)在图1中，请写出∠A，∠B，∠C，∠D之间的数量关系，并说明理由；(2)如图2，计算∠A+∠B+∠C+∠D+∠E+∠F的度数．
∠A+∠D=∠B+∠C
∠A+∠B+∠C+∠D+∠E+∠F=360°
三 角 形
多 边 形 的 内 角 和
整体思想转化思想方程思想模型思想
1. 一个多边形的内角和不可能是（ ）A.1800° B.540 ° C.720 ° D.810 °
2. 一个多边形从一个顶点可引对角线3条，则这个多边形的 内角和等于（ ）A.360° B.540 ° C.720 ° D.900 °
3. 一个多边形的内角和是360°，这个多边形是(　　)　　　　　　　　　　　　　　　　A．三角形 B．四边形 C．六边形 D．不能确定
4. 一个正多边形的内角和为720°，则这个正多边形的每一个内角等于______．
5. 如图所示，小华从点A出发，沿直线前进10米后左转24°，再沿直线前进10米，又向左转24°，…，照这样走下去，他第一次回到出发地点A时，走的路程一共是________米．
6. 一个多边形的内角和为1800°，截去一个角后，求得到的多边形的内角和.
解：∵ 1800÷180＝10，∴ 原多边形边数为10＋2＝12.∵ 一个多边形截去一个内角后，边数可能减1，可能不变，也可能加1，∴ 新多边形的边数可能是11，12，13，∴ 新多边形的内角和可能是1620°，1800°，1980°.