






- 新教材2023_2024学年高中数学第二章平面解析几何2.3圆及其方程2.3.2圆的一般方程课件新人教B版选择性必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第二章平面解析几何2.3圆及其方程2.3.3直线与圆的位置关系课件新人教B版选择性必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第二章平面解析几何2.4曲线与方程课件新人教B版选择性必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第二章平面解析几何2.5椭圆及其方程2.5.1椭圆的标准方程课件新人教B版选择性必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第二章平面解析几何2.5椭圆及其方程2.5.2椭圆的几何性质课件新人教B版选择性必修第一册 课件 0 次下载
人教B版 (2019)选择性必修 第一册2.3.4 圆与圆的位置关系背景图ppt课件
展开1.理解圆与圆的位置关系的五种类型;2.掌握圆与圆的位置关系的代数判断方法与几何判断方法;3.能用圆的对称性灵活处理问题.
基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
1.几何法:若两圆的半径分别为r1,r2,两个圆的圆心距为d,则两圆的位置关系的判断方法如下:
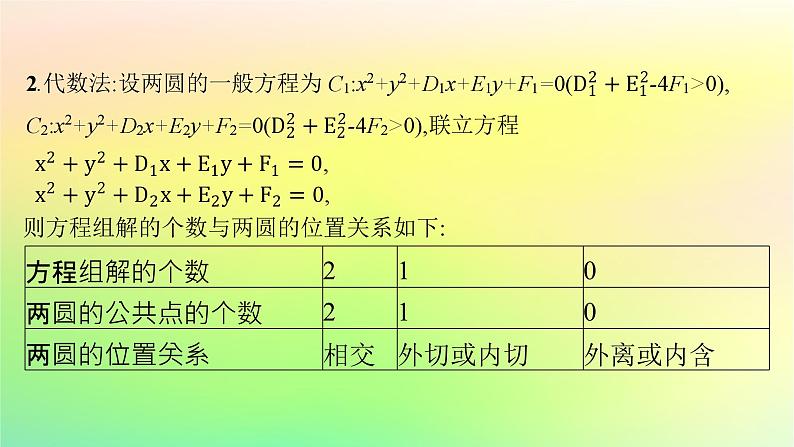
则方程组解的个数与两圆的位置关系如下:
名师点睛1.利用代数法判断两圆位置关系时,当方程组无解时,只能判断两圆相离,无法判断是外离还是内含;当方程组有一解时,只能判断两圆相切,无法判断是外切还是内切.2.在判断两圆的位置关系时,优先使用几何法.3.当两圆半径相等时,两圆只有外离、外切、相交三种位置关系.
过关自诊1.判断正误.(正确的画√,错误的画×)(1)如果两圆的圆心距小于两圆的半径之和,则两圆相交.( )(2)若两圆有公共点,则|r1-r2|≤d≤r1+r2.( )(3)如果两个圆的方程组成的方程组只有一组实数解,则两圆外切.( )2.当两圆外离、外切、相交、内切、内含时,两圆的公切线分别有几条?
解 两圆外离时,公切线有4条,外切时有3条,相交时有2条,内切时有1条,内含时没有公切线.
探究点一 两圆位置关系的判断
【例1】 [人教A版教材例题]已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
解 (方法一)将圆C1与圆C2的方程联立,得到方程组
把上式代入①,并整理,得x2-2x-3=0.④
方程④的根的判别式Δ=(-2)2-4×1×(-3)=16>0,所以,方程④有两个不相等的实数根x1,x2,把x1,x2分别代入方程③,得到y1,y2.因此圆C1与圆C2有两个公共点A(x1,y1),B(x2,y2),这两个圆相交.(方法二)把圆C1的方程化成标准方程,得(x+1)2+(y+4)2=25,圆C1的圆心是(-1,-4),半径r1=5.把圆C2的方程化成标准方程,得(x-2)2+(y-2)2=10,圆C2的圆心是(2,2),半径
变式探究若本例中条件不变,所求改为“求圆C1与圆C2的公切线条数”,结论又如何?
解 根据例题中结论☉C1与☉C2相交,则由平面几何知识可知,公切线条数为2.
规律方法 判断两圆的位置关系常用两种方法几何法和代数法,但一般情况下用几何法,即用两圆半径和圆心距之间的关系来刻画,此种方法形象直观,关键是明确圆心和半径,再套用圆与圆位置关系的关系式进行求解或判断.
变式训练1已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,当m为何值时,分别满足下列情况:(1)圆C1与圆C2外切;(2)圆C1与圆C2内含.
解 易得圆C1:(x-m)2+(y+2)2=9,圆心C1(m,-2),半径r1=3;圆C2:(x+1)2+(y-m)2=4,圆心C2(-1,m),半径r2=2.
探究点二 两圆的公共弦问题
【例2】 已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0.(1)判断两圆是否相交,若相交,求出公共弦所在的直线方程;若不相交,请说明理由.(2)求公共弦的长度.
解 (1)相交.将两圆方程配方化为标准方程,则C1:(x-1)2+(y+5)2=50,C2:(x+1)2+(y+1)2=10,
∴|r1-r2|<|C1C2|
(方法二)设两圆相交于点A,B,则A,B两点满足方程组
规律方法 1.当两圆相交时,公共弦所在的直线方程的求法若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在的直线方程为(D1-D2)x+(E1-E2)y+F1-F2=0.2.公共弦长的求法(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
变式训练2[人教A版教材习题]求圆x2+y2-4=0与圆x2+y2-4x+4y-12=0的公共弦的长.
得y=x+2.把y=x+2代入x2+y2-4=0,得x2+2x=0,解得x1=-2,x2=0.于是有y1=0,y2=2,所以两圆交点坐标分别是A(-2,0),B(0,2).
(方法二)由方程x2+y2-4=0与x2+y2-4x+4y-12=0,消去二次项,得y=x+2.
如图,过点O作弦AB的垂线,垂足是M.因为圆心为O的圆的半径长是2,所以|OA|=2.
探究点三 圆系方程的应用
【例3】 [人教A版教材习题]求经过点M(2,-2)以及圆x2+y2-6x=0与x2+y2=4交点的圆的方程.
(方法二)设经过圆x2+y2-6x=0与x2+y2=4交点的圆的方程为x2+y2-6x+λ(x2+y2-4)=0.①把点M(2,-2)的坐标代入①,得22+(-2)2-6×2+λ[22+(-2)2-4]=0,解得λ=1.把λ=1代入①,并化简得x2+y2-3x-2=0.所以所求圆的方程为x2+y2-3x-2=0.
规律方法 1.当经过两圆的交点时,圆的方程可设为(x2+y2+D1x+E1y+F1)+λ(x2+y2+D2x+E2y+F2)=0,然后用待定系数法求出λ即可.2.当给出的方程结构中参数比较分散时,要注意将含参数的合并在一起,进而讨论过定点或交点问题.
变式训练3求圆心在直线x-y-4=0上,且过圆x2+y2-4x-6=0和圆x2+y2-4y-6=0的交点的圆的方程.
解 (方法一)设经过两圆交点的圆系方程为x2+y2-4x-6+λ(x2+y2-4y-6)=0(λ≠-1),
所以所求圆的方程为x2+y2-6x+2y-6=0.
所以两圆x2+y2-4x-6=0和x2+y2-4y-6=0的交点坐标分别为A(-1,-1),B(3,3),线段AB的垂直平分线所在的直线方程为y-1=-(x-1).
即所求圆的圆心坐标为(3,-1),
1.圆(x-3)2+(y+2)2=1与圆x2+y2-14x-2y+14=0的位置关系是( )A.外切B.内切C.相交D.外离
解析 圆x2+y2-14x-2y+14=0变形为(x-7)2+(y-1)2=36,圆心坐标为(7,1),半径为r1=6;圆(x-3)2+(y+2)2=1的圆心坐标为(3,-2),半径为r2=1,所以圆心距
2.圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则AB的垂直平分线的方程是( )A.x+y+3=0B.2x-y-5=0C.3x-y-9=0D.4x-3y+7=0
解析 AB的垂直平分线过两圆的圆心,把圆心(2,-3)代入,即可排除A,B,D.
3.已知圆O1:x2+y2=16和圆O2:x2+y2-6mx-8my+24m2=0有且仅有4条公切线,则实数m的取值范围是( )A.(-∞,-1)∪(1,+∞)B.(-1,1)C.(-∞,-2)∪(3,+∞)D.(-2,3)
解析 圆O1:x2+y2=16的圆心O1(0,0),半径r1=4,圆O2:x2+y2-6mx-8my+24m2=0的圆心O2(3m,4m),半径r1=|m|.根据题意可得,圆O1,圆O2相离,则|O1O2|>r1+r2,即5|m|>4+|m|,∴m∈(-∞,-1)∪(1,+∞).故选A.
4.圆C1:x2+y2-2x-8=0与圆C2:x2+y2+2x-4y-4=0的公共弦长为 .
解析 由圆C1与圆C2的公共弦所在的直线l的方程为x-y+1=0,得点C1(1,0)
5.已知圆C1:x2+y2+4x+1=0和圆C2:x2+y2+2x+2y+1=0,求以圆C1与圆C2的公共弦为直径的圆的方程.
解 由两圆的方程相减,得公共弦所在直线的方程为x-y=0.∵圆C1:(x+2)2+y2=3,圆C2:(x+1)2+(y+1)2=1,圆心C1(-2,0),C2(-1,-1),
人教B版 (2019)选择性必修 第一册2.3.4 圆与圆的位置关系课文ppt课件: 这是一份人教B版 (2019)选择性必修 第一册2.3.4 圆与圆的位置关系课文ppt课件,共30页。PPT课件主要包含了新知初探·自主学习,课堂探究·素养提升,d>r1+r2,d=r1+r2,d=r1-r2,d<r1-r2,内切或外切,外离或内含,答案C,答案B等内容,欢迎下载使用。
人教B版 (2019)选择性必修 第一册2.5.1 椭圆的标准方程多媒体教学课件ppt: 这是一份人教B版 (2019)选择性必修 第一册2.5.1 椭圆的标准方程多媒体教学课件ppt,共38页。PPT课件主要包含了目录索引等内容,欢迎下载使用。
高中数学人教B版 (2019)选择性必修 第一册2.3.1 圆的标准方程图文ppt课件: 这是一份高中数学人教B版 (2019)选择性必修 第一册2.3.1 圆的标准方程图文ppt课件,共30页。PPT课件主要包含了目录索引等内容,欢迎下载使用。













