数学八年级下册1.2 直角三角形的性质与判定（Ⅱ）同步练习题

A[勾股定理的逆定理]

一、选择题

1.下列长度的三条线段能组成直角三角形的是 (　　)

A.3,4,5 B.2,3,4 C.4,6,7 D.5,11,12

2.若一个三角形的三边长a,b,c满足(a+b)2=c2+2ab,则这个三角形是 (　　)

A.等边三角形  B.钝角三角形 

C.等腰直角三角形  D.直角三角形

3.下列各组数中,不是勾股数的是 (　　)

A.5,12,13 　　　　 B.7,24,25

C.8,12,15 　　　　 D.3k,4k,5k(k为正整数)

4.如图,在正方形网格中有一个△ABC(A,B,C均在格点上),若小方格的边长均为1,则△ABC是 (　　)

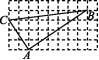
A.直角三角形  B.锐角三角形

C.钝角三角形  D.以上都不正确

5.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何.”这道题讲的是:有一块三角形沙田,三条边长分别为5里、12里、13里,问这块沙田面积有多大.题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为              (　　)

A.7.5平方千米  B.15平方千米

C.75平方千米  D.750平方千米

二、填空题

6.(2021长沙开福区期中)已知在△ABC中,AC=8,AB=10,BC=6,D是AB的中点,则CD=　　　　. 

7.如果△ABC的三边长分别为5,12,x,那么当x为　　　　　时,△ABC是直角三角形. 

三、解答题

8.已知在△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,试根据下列条件,判断△ABC是不是直角三角形,若是,请指出哪一个角是直角.

(1)a=,b=2,c=;

(2)a=5,b=7,c=9.

9.在△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,若=,求证:△ABC是直角三角形.

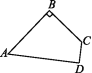
10.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.

(1)判断∠D是不是直角,并说明理由;

(2)求四边形ABCD的面积.

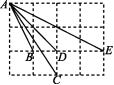
11.如图所示,在4×3的网格中,每个小正方形的边长都是1,有从点A出发的四条线段AB,AC,AD,AE,它们的另一个端点B,C,D,E均在格点上.

(1)求出线段AB,AC,AD,AE的长度(结果保留根号);

(2)在AB,AC,AD,AE四条线段中,是否存在三条线段可以构成直角三角形?如果存在,请指出是哪三条线段,并说明理由.

图   

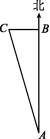
12.如图,一艘在海上朝正北方向航行的轮船,从点A处航行了240海里到达点B处时方位仪坏了,凭经验,船长指挥船左转一定角度后,继续航行70海里到达点C处,此时A,C之间的距离为250海里,请你判断船转弯后,是否沿正西方向航行.

 [阅读理解与探究性问题] 在一次“探究性学习”课中,老师设计了如下数表:

(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a=　　　　,b=　　　　,c=　　　　; 

(2)猜想以a,b,c为边长的三角形是不是直角三角形,证明你的猜想;

(3)显然,满足这样关系的整数a,b,c我们把它们叫作　　　　　数,请再写出一组这样的数:　　　　　(不同于表格中已出现的数组). 

问题探究:已知三角形的三边长分别为a,b,c,且a=m-1,b=2,c=m+1(m>1).请你判断这个三角形的形状,能否找出一个以a,b,c为边长的三角形,使它的最小边长不小于20,不大于22,另两边长的差为2,且三边长均为正整数?

答案

1.A　2.D　3.C

4. A　利用勾股定理求出AC=,AB=,BC=,所以有AC2+AB2=BC2,所以△ABC是直角三角形.

5. A　∵52+122=132,∴这个三角形为直角三角形.又∵5里=2500米=2.5千米,12里=6000米=6千米,∴该沙田的面积为×6×2.5=7.5(平方千米).

6. 5

 ∵AC=8,AB=10,BC=6,

∴AC2+BC2=AB2,∴∠C=90°.

∵D为AB的中点,

∴CD=AB=×10=5.

7. 13或

 若5,12,x中,x最大,

则x2=52+122,

即当x=13时,△ABC为直角三角形;

若5,12,x中,12最大,则122=x2+52,

即当x=时,△ABC为直角三角形.

[点评] 此题要注意将x分别作为直角边长和斜边长进行分类讨论.

8.解:(1)∵a=,b=2,c=,

∴a2=3,b2=8,c2=5.

∵3+5=8,∴a2+c2=b2,

∴△ABC是直角三角形,且∠B=90°.

(2)∵a=5,b=7,c=9,

∴a2=25,b2=49,c2=81.

∵25+49=74≠81,

∴△ABC不是直角三角形.

9.证明:∵=,

∴ac=(a+b+c)(a-b+c)=[(a2+2ac+c2)-b2],

∴2ac=a2+2ac+c2-b2,∴a2+c2=b2,

∴△ABC是直角三角形.

10.解:(1)∠D是直角.

理由:连接AC.∵∠B=90°,

∴AC2=AB2+BC2=202+152=625.

∵AD2+CD2=242+72=625,

∴AC2=AD2+CD2,

∴△ADC是直角三角形,且∠D是直角.

(2)∵四边形ABCD的面积=△ABC的面积+△ADC的面积,

∴四边形ABCD的面积=AB·BC+AD·CD=×20×15+×24×7=234.

11.解:(1)AB==,AC==,AD==2,AE==2.

(2)线段AB,AC,AD可以构成直角三角形.理由:∵AD2+AB2=AC2,∴由勾股定理的逆定理可得线段AB,AC,AD可以构成直角三角形.

12.解:∵AB=240海里,BC=70海里,AC=250海里,

∴AB2+BC2=AC2,∴∠ABC=90°,

∴船转弯后,沿正西方向航行.

[素养提升]

解:(1)n2-1　2n　n2+1　

(2)猜想:以a,b,c为边长的三角形是直角三角形.

证明:∵a2+b2=(n2-1)2+(2n)2=n4+2n2+1,

c2=(n2+1)2=n4+2n2+1,

∴a2+b2=c2,

∴以a,b,c为边长的三角形是直角三角形.

(3)勾股　a=35,b=12,c=37(答案不唯一)

问题探究:∵a2+b2=(m-1)2+(2)2=m2-2m+1+4m=m2+2m+1=(m+1)2,c2=(m+1)2,

∴a2+b2=c2,

∴这个三角形是直角三角形.

能找出一个以a,b,c为边长的三角形,使它的最小边长不小于20,不大于22,另两边长的差为2,且三边长均为正整数.

当b=20时,2=20,∴m=100,

∴a=m-1=99,c=m+1=101;

当b=22时,2=22,∴m=121,

∴a=m-1=120,c=m+1=122.