初中数学湘教版八年级下册1.2 直角三角形的性质与判定（Ⅱ）课文配套ppt课件

课题名

直角三角形的性质和判定Ⅱ

教学目标

1.知识与技能： 探索并掌握直角三角形判别的方法——勾股定理逆定理，并能通过三角形三边的数量关系来判断它是否为直角三角形。

2.过程与方法： 通过“创设情境——实验验证——理论释意——应用”的探索过程，让学生感受知识的乐趣。

3.情感态度和价值观：通过合作交流学习的发展体验获取数学知识的感受；通过对勾股定理逆定理的探究，激发学生学习数学的兴趣和创新精神，并培养学生数形结合的思想。

教学重点

理解和应用勾股定理的逆定理判定直角三角形的方法。

教学难点

理解勾股定理的逆定理。

教学准备

教师准备：制作《直角三角形的性质和判定Ⅱ》课件。

学生准备：预习《直角三角形的性质和判定Ⅱ》，并准备作图工具。

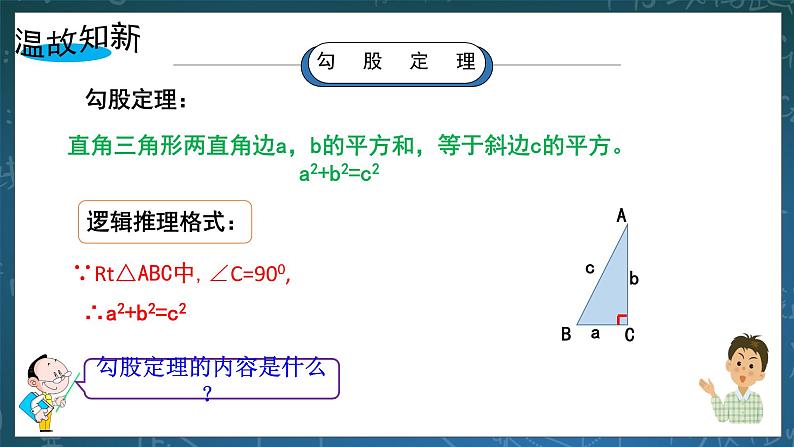
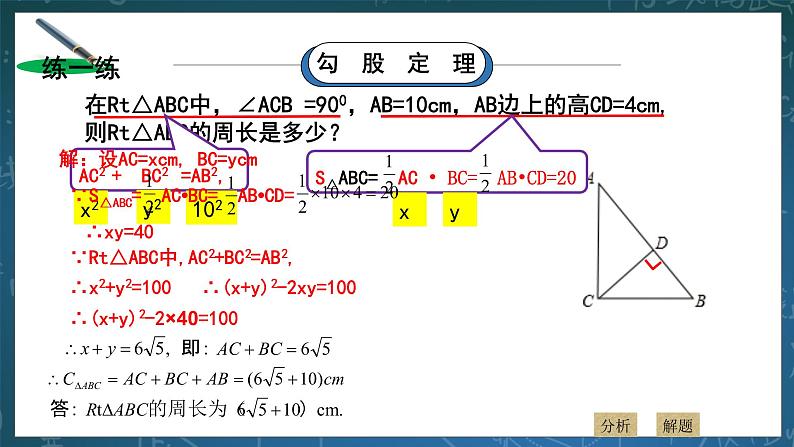
教学过程

一、 温故知新

1.教师提问：勾股定理的内容是什么？

学生回答：直角三角形两直角边a，b的平方和，等于斜边c的平方,即：a2+b2=c2

逻辑推理格式：

∵Rt△ABC中,∠C=900,

∴a2+b2=c2

2.在Rt△ABC中，∠ACB =900，AB=10cm，AB边上的高CD=4cm,则Rt△ABC的周长是多少？

分析：设AC=xcm,BC=ycm,在Rt△ABC中，根据勾股定理可得：x2+y2=102,根据面积公式可得：xy=AB•CD,即xy=40.要求Rt△ABC的周长（x+y+10）的值，只需求出(x+y)的值就可以了。

解：设AC=xcm, BC=ycm

∵S△ABC=AC•BC=AB•CD=×10×4=20,      ∴xy=40

∵Rt△ABC中,AC2+BC2=AB2,∴x2+y2=100      ∴(x+y)2-2xy=100

∴(x+y)2-2×40=100     ∴x+y=6  即：AC+BC=6

∴C△ABC=AC+BC+AB=10+6 (cm)

二、 情境导入

1. 我们学了哪些方法判定一个三角形是直角三角形？

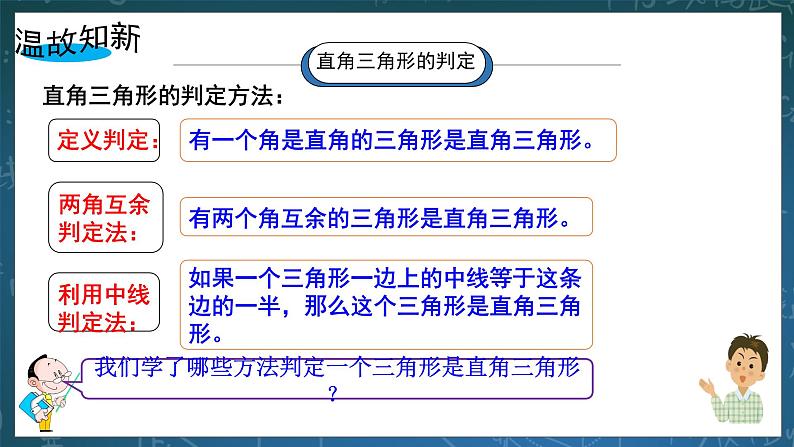
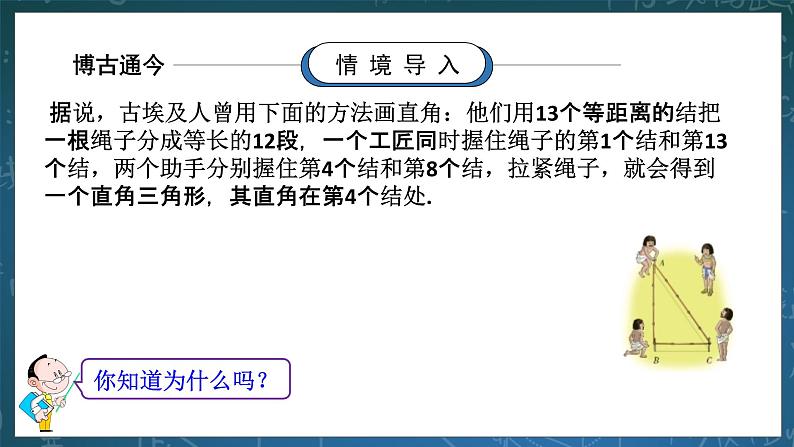
答：我们学过判定一个三角形是直角三角形的方法有①定义判定——有一个角是直角的三角形是直角三角形；②两角互余判定法——有两个角互余的三角形是直角三角形；③利用中线判定法——如果一个三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形。

2.据说，古埃及人曾用下面的方法画直角：他们用13个等距离的结把一根绳子分成等长的12段，一个工匠同时握住绳子的第1个结和第13个结，两个助手分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，其直角在第4个结处.你知道为什么吗？         

三、新知讲授

（活动一）:探究——勾股定理的逆定理

1. 勾股定理的逆命题什么？

逆命题:如果三角形的三条边长a,b,c满足关系：a2+b2=c2，那么这个三角形是直角三角形。

2. 如图，在△ABC中，AB=c,BC=a,AC=b，且a²+b2=c2，那么△ABC是直角三角形吗？

分析 ：如果我们能构造一个直角三角形，这个直角三角形的两直角边长分别为a,b，则斜边长一定为c,然后证明△ABC与所构造的直角三角形全等，即可得△ABC是直角三角形。

解：作Rt△A/B/C/,使∠C/=900, B/C/=a, A/C/=b.

在Rt△A/B/C/中，根据勾股定理得： A/B/2=c2+b2,

∵c2+b2=c2,∴ A/B/2=c2.∴ A/B/=c.

在△ABC和△A/B/C/中，

∵BC=B/C/=a,AC=A/C/=b,AB=A/B/=c,

∴△ABC≌△A/B/C/.  ∴∠C=∠C/=90°.∴△ABC是直角三角形.

§解题技巧：先构造满足某些条件的图形，然后根据所求证的图形与所构造图形之间的关系，完成证明，这也是常用的问题解决策略。

（活动二）:总结——勾股定理的逆定理

1.勾股定理的逆定理：如果三角形的三条边长a，b, c满足关系: a2+b2=c2，那么这个三角形是直角三角形.

2.逻辑推理格式：

∵△ABC的三条边长a，b, c满足关系:a2+b2=c2

∴△ABC是直角三角形，且∠ACB=900

（活动三）:做一做——典例分析

例3    判断由线段a,b,c组成的三角形是不 是直角三角形。

   (1)a=6,b=8,c=10;                            (2)a=12,b=20,c=15.

解：∵a2+b2=62+82=100，                     解：∵a2+c2=122+152=400

      c2=102=100                                 b2=202=400

∴a2+b2=c2                                                                          ∴a2+c2=b2

∴这个三角形是直角三角形                  ∴这个三角形是直角三角形

§解题技巧：已知三角形的三边，判定直角三角形，只要看两条较短边长的平方和是否等于最长边的平方.

（活动四）:记一记——勾股数

1. 满足a2+b2=c2的三个正整数称为勾股数。

2.识记常见的勾股数：

① 3，4，5；   6，8，10；   9，12，15； ……

② 5，12，13； 10，24，26； 15，36，39；……

③ 8，15，17； 16，30，34；  ……

3.勾股数中的规律：将一组勾股数的每一个数都扩大（或缩小）相同倍数，仍构成勾股数。

（活动五）:应用——典例分析

例4  如图，在△ABC中，已知AB=10, BD=6, AD=8，AC=17.

求DC的长.

解：∵在△ABC中，AB=10, BD=6, AD=8

∴BD2+AD2=AB2

∴△ABD是直角三角形，且∠ADB=900.

∴∠ADC=1800-∠ADB=900.

∴在Rt△ADC中，DC===15

三、课堂小测：

1.判断由线段a, b, c组成的三角形是不是直角三角形.

(1) a=8, b=15, c=17;             (2) a=10，b=24, c=25;

解：∵a2+b2=82+152=289，      解：∵a2+b2=102+242=676，

c2=172=289                  c2=252=625

∴a2+b2=c2                        ∴a2+b2≠c2

∴这个三角形是直角三角形.     ∴这个三角形不是直角三角形.

(3) a=4, b=5, c=

解：∵a2+b2=42+52=41，

c2=（ ）2=41

∴a2+b2=c2

∴这个三角形是直角三角形

2.   如图，在边长为4的正方形ABCD中，F为CD的中点，E是BC上一点，且EC=BC

求证: △AEF是直角三角形.

解：由题意可得：AB=AD=BC=DC=4,DF=CF=DC=2,

EC=BC=1,BE=BC-EC=3,∠B=∠D=∠C=900.

∵在Rt△ABE中，AE2=AB2+BE2=42+32=25

在Rt△ADF中，AF2=AD2+DF2=42+22=20

在Rt△FCE中，EF2=CF2+CE2=22+12=5

∴EF2+AF2=AE2

∴△AEF是直角三角形

四、你的收获：

1.勾股定理逆定理:如果三角形的三条边长a，b, c满足关系: a2+b2=c2，那么这个三角形是直角三角形.

2.已知三角形的三边，判定直角三角形，只要看两条较短边长的平方和是否等于最长边的平方

3.判定一个三角形是直角三角形的方法：

①定义判定；②两角互余判定法；③利用中线判定法；④勾股定理的逆定理。

布置作业

课堂作业：P16  习题1.2 第5、9题。

家作：P16  习题1.2第6、7、8题并预习P19~20《直角三角形全等的判定》。

板书设计

教学反思

本节课从复习复习勾股定理、直角三角形的判定方法开始，引出古人对直角三角形的判定方法，然后通过逻辑推理探究了勾股定理的逆定理，并通过，学习运用勾股定理的逆定理解决实际问题的方法和技巧。其中，运用勾股定理的逆定理判定直角三角形的方法和技巧是教学的难点。在教学中，通过实例，变抽象为具体，从而化难为易，激发学生兴趣，培养学生的分析能力和逻辑推理能力，加深学生对知识的理解的运用。